
কার্য, ক্ষমতা ও শক্তি
বাইরে থেকে কোন বস্তুর ওপর বল প্রয়োগ করলে যদি বস্তুর অবস্থানের বিবর্তন হয় তাহলে প্রযুক্ত বল কার্য করেছে বলে ধরা হয় । কিন্তু বল প্রয়োগ করলেও যদি বস্তুটির অবস্থানের কোনো পরিবর্তন না হয় তাহলে সে ক্ষেত্রে প্রযুক্ত বল কোন কার্য করেছে বলে ধরা হয় না । বল এবং সরণ ভেক্টর রাশি হলেও কার্য একটি স্কেলার রাশি কার্যের মান আছে ...

গতি সংক্রান্ত কয়েকটি রাশি
যদি কোন বস্তু একটি নির্দিষ্ট দিকে স্থান পরিবর্তন করে তবে সেই পরিবর্তনকে বস্তুটির সরণ বলে । অর্থাৎ নির্দিষ্ট দিকে কোন বস্তুর অবস্থানের পরিবর্তন কে স্মরণ বলে । বস্তুটির প্রথম এবং শেষ অবস্থান একটি সরলরেখা দিয়ে যোগ করলে যে রৈখিক দূরত্ব পাওয়া যায় তাই হলো সরণের পরিমাপ ।
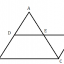
ভেদক ও মধ্যবিন্দু সংক্রান্ত অংকের সমাধান
ভেদক ও মধ্যবিন্দু সংক্রান্ত অংকের সমাধান ( Prove and Solution of Transversal and Mid-Point Theorem Related Problems)
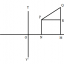
লেখচিত্রের সাহায্যে যেকোনো দুটি বিন্দুর মধ্যবর্তী দূরত্ব নির্ণয়
মনে করি P ও Q দুটি বিন্দু উহাদের স্থানাঙ্ক হল যথাক্রমে [EQUATION-1] এবং [EQUATION-2] . P ও Q যোগ করা হল এখন আমাদের PQ এর দূরত্ব বা দৈর্ঘ্য নির্ণয় করতে হবে।
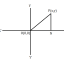
লেখচিত্রের সাহায্যে মূলবিন্দু থেকে যেকোনো বিন্দুর দূরত্ব নির্ণয়
মনে করি XOX' ও YOY' সরলরেখাদ্বয় লম্বভাবে পরস্পরকে O বিন্দুতে ছেদ করেছে। XOX' ও YOY' এইদুটি স্থানাঙ্ক রেখা বা Co-Ordinate axes এবং O হল মূলবিন্দু ( Origin ) ।
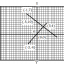
লেখচিত্রের সাহায্যে রৈখিক সহসমীকরণ সমাধান
মনে করি 3x + 4y = 25 এবং 4x - 3y = 0 দুটি সমীকরণ এদেরকে আমাদের সমাধান করতে হবে। দেখা যাচ্ছে দুটি সরলরেখার একটি সাধারণ বিন্দু হল (3,4) . অর্থাৎ দুটি সরলরেখা পরস্পরকে (3,4) বিন্দুতে ছেদ করেছে।

বিভিন্ন প্রকার রাশিমালা
বীজগাণিতিক রাশিমালা ( Algebraical Expression ) দুইপ্রকার সরল রাশি ( Simple Expression ) বা এক পদীয় ( Monomial ) জটিল রাশি ( Complex Expression ), জটিল রাশি ( Complex Expression ) আবার তিন প্রকার

বহুপদী সংখ্যামালার ধর্ম
দুটি বহুপদীয় রাশির যোগফল , বিয়োগফল ও গুণফল সর্বদা বহুপদীয় রাশি হয়। যদি কোনো বহুপদী রাশিমালা অপেক্ষক f(x) এমন হয় যে f(a) = 0 তখন অপেক্ষকটি ( x-a ) দ্বারা বিভাজ্য হবে। অর্থাৎ বহুপদী সংখ্যামালা সর্বদাই তার উৎপাদক দ্বারা বিভাজ্য হবে।

ভাগশেষ উপপাদ্য
f(x) একটি বহুপদী সংখ্যামালা যার মাত্রা Equation1 এবং a যেকোনো একটি বাস্তব সংখ্যা। f(x) কে ( x-a ) দ্বারা ভাগ করলে ভাগশেষ হবে f(a) .

গুণনীয়ক উপপাদ্য (Factor Theorem)
যদি f(x) কোনো একটি বহুপদী সংখ্যামালা যার মাত্রা Equation 1 এবং a যেকোনো একটি বাস্তব সংখ্যা হয় , তাহলে

বহুপদী সংখ্যামালা সংক্রান্ত অংকের সমাধান
বহুপদী সংখ্যামালা সংক্রান্ত অংকের সমাধান (Solution of Polynomials )
সামন্তরিকের ষষ্ঠ উপপাদ্য
কোনো চতুর্ভুজের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করলে চতুর্ভুজটিকে সামান্তরিক বলে।
সামন্তরিকের পঞ্চম উপপাদ্য
পঞ্চম উপপাদ্য : সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে।
সামন্তরিকের চতুর্থ উপপাদ্য
কোনো চতুর্ভুজের বিপরীত কোণগুলি সমান হলে , চতুর্ভুজটি একটি সামান্তরিক হবে।
সামন্তরিকের তৃতীয় উপপাদ্য
কোনো চতুর্ভুজের বিপরীত বাহুগুলি সমান হলে , চতুর্ভুজটি একটি সামান্তরিক হবে।
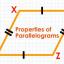
সামন্তরিকের দ্বিতীয় উপপাদ্য
কোনো সামান্তরিকের (i) প্রতিটি কর্ণ সামান্তরিককে দুটি সর্বসম ত্রিভুজে বিভক্ত করে (ii) বিপরীত বাহুগুলির দৈর্ঘ্য সামন। (iii) বিপরীত কোণ গুলি মানে সমান।
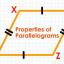
সামন্তরিকের প্রথম উপপাদ্য
কোনো চতুর্ভুজের একজোড়া বিপরীত বাহু সমান এবং সমান্তরাল হলে অপর জোড়া বিপরীত বাহুও সমান এবং সমান্তরাল হবে অর্থাৎ চতুর্ভুজটি একটি সামান্তরিক হবে।

করণীর কার্যপ্রণালী (Operations with Surds)
করণীর যোগফল ও বিয়োগফল(Addition and subtraction of Surds): করণীর যোগফল বা বিয়োগফল নির্ণয় করতে হলে নিম্নলিখিত পদ্ধতি অবলম্বন করতে হবে ।

বিভিন্ন প্রকার করণী (Different types of Surds)
সমমূলীয় ও অসমমূলীয় করণী (Equiradical and unequiradical surds): একাধিক করণী ক্রম সমান হলে তাদের সমমূলীয় করণী বলে ।

দ্বিঘাত করণীর কয়েকটি ধর্ম (Properties of Quadratic Surds)
1. দুটি অসদৃশ দ্বিঘাত করণীর গুণফল মূলদ রাশি হতে পারে না, 2. একটি সরল দ্বিঘাত করণী কখনও একটি মূলদ রাশি ও একটি দ্বিঘাত করণীর যোগফল বা অন্তরফল সমান হতে পারে না ।, 3. একটি সরল দ্বিঘাত করণী কখনও দুটি অসদৃশ সরল দ্বিঘাত করণীর যোগফল বা অন্তরফলের সমান হতে পারে না ।
