লেখচিত্রের সাহায্যে রৈখিক সহসমীকরণ সমাধান
মনে করি 3x + 4y = 25 এবং 4x - 3y = 0 দুটি সমীকরণ এদেরকে আমাদের সমাধান করতে হবে ।
সমাধান : এখন
3x+4y=25⇒4y=25−3x⇒y=25−3x4.......(i)
(i) এর থেকে আমরা পাই
| x | 3 | -1 | -5 |
| y=25−3x4 | 4 | 7 | 10 |
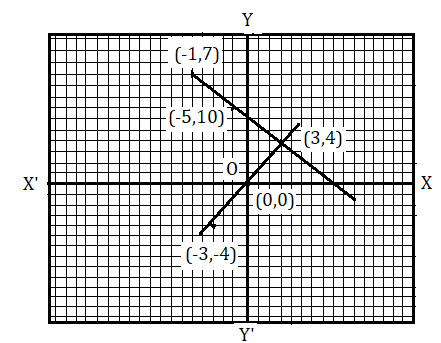
3x + 4y = 25 সরলরেখা থেকে যে সমাধান বিন্দুগুলি পাই তাহল (3,4) , (-1,5) এবং (-5,10)
আবার
4x−3y=0⇒3y=4x⇒y=4x3.......(ii)
(ii) এর থেকে আমরা পাই
| x | 0 | 3 | -3 |
| y=4x3 | 0 | 4 | -4 |
4x - 3y = 0 সরলরেখা থেকে যে সমাধান বিন্দুগুলি পাই তাহল (0,0) , (3,4) এবং (-3,-4)
দেখা যাচ্ছে দুটি সরলরেখার একটি সাধারণ বিন্দু হল (3,4) . অর্থাৎ দুটি সরলরেখা পরস্পরকে (3,4) বিন্দুতে ছেদ করেছে। অতএব সরলরেখা দুটি কে সমাধান করলে আমরা পাবো x = 3 , y = 4 .
এর থেকে আমরা বলতে পারি রৈখিক সহসমীকরণের সমাধান সম্ভব যদি তারা পরস্পরকে ছেদ করে নতুবা নয়।
উপরের আলোচনা থেকে দেখা যাচ্ছে যে বিন্দুগুলির স্থানাঙ্ক জানা থাকলে সেগুলি যোগ করে বিভিন্ন সমতলিক জ্যামিতিক চিত্র পাওয়া যায় । আবার বিভিন্ন বীজগাণিতিক দুই চলবিশিষ্ট রৈখিক সহসমীকরণ জ্যামিতিক আকার সম্পর্কে ঠিক মতো ধারণা করা যায় । এইভাবে বীজগণিতের সাহায্যে বিভিন্ন জ্যামিতিক আকারের ধারণা গড়ে ওঠা কে স্থানাঙ্ক জ্যামিতি ( Co-ordinate Geometry ) বলা হয় । অর্থাৎ স্থানাঙ্ক জ্যামিতিতে বীজগণিতের সাহায্যে ধারণা করতে পারি। তাই স্থানাঙ্ক জ্যামিতি ব্যাপকতরভাবে বিজ্ঞানের বিভিন্ন শাখায় ব্যবহার করা হয় ।
*****