লেখচিত্রের সাহায্যে মূলবিন্দু থেকে যেকোনো বিন্দুর দূরত্ব নির্ণয়
মনে করি XOX' ও YOY' সরলরেখাদ্বয় লম্বভাবে পরস্পরকে O বিন্দুতে ছেদ করেছে। XOX' ও YOY' এইদুটি স্থানাঙ্ক রেখা বা Co-Ordinate axes এবং O হল মূলবিন্দু ( Origin ) ।
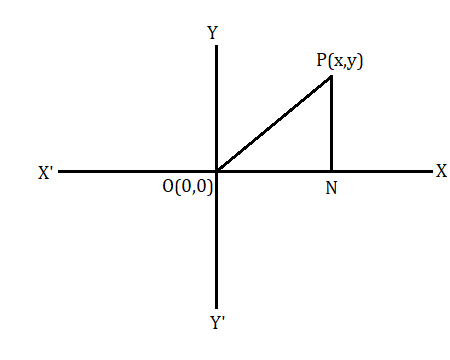 এই সমতলে কোনো একটি বিন্দু P এর স্থানাঙ্ক ধরা হল (x,y) . তাহলে মূলবিন্দু O(0,0) থেকে P(x,y) বিন্দুর দূরত্ব আমাদের নির্ণয় করতে হবে।
এই সমতলে কোনো একটি বিন্দু P এর স্থানাঙ্ক ধরা হল (x,y) . তাহলে মূলবিন্দু O(0,0) থেকে P(x,y) বিন্দুর দূরত্ব আমাদের নির্ণয় করতে হবে।
এখন P বিন্দু থেকে OX এর উপর PN লম্ব টানা হল এবং OP যুক্ত করা হল।
অতএব ON = x এবং PN = y .এখন OPN সমকোণী ত্রিভুজ। অতএব পিথাগোরাসের উপপাদ্য অনুযায়ী
OP2=ON2+PN2=x2+y2
অতএব OP=√x2+y2 একক
অতএব মূলবিন্দু O(0,0) থেকে P(x,y) বিন্দুর দূরত্ব হল √x2+y2
যেহেতু দুটি বিন্দুর মধ্যে দূরত্ব কখনো ঋণাত্মক হয়না সেইকারণে আমরা কেবল ধনাত্মক মানই ধরব।