লেখচিত্র (Graph)
সূচনা ( Introduction )
লেখচিত্র বলতে কি বোঝায় এবং ইহার প্রয়োজনীয়তা সম্মন্ধে তাহাদের স্পষ্ট ধারণা থাকা আবশ্যক । প্রাত্যহিক জীবনে লেখচিত্রের ব্যবহার অপরিহার্য। রোগীর তাপমাত্রা হ্রাস বৃদ্ধি , শিল্প প্রতিষ্ঠানে উৎপাদন হার , দ্রব্যমূলের হ্রাস বৃদ্ধি ইত্যাদি বহু তথ্য এবং পাটিগণিতের বিবিধ প্রশ্নের এই লেখচিত্রের সাহায্যে প্রকাশ ও সমাধান করা যায় । অতএব লেখচিত্র হল বিবিধ ঘটনার , তথ্য বা সমস্যার চিত্র রূপ ।
স্থানাঙ্ক জ্যামিতি ( Coordinate Geometry ) : একই তলস্থিত কোনো বিন্দুর নির্দিষ্ট অবস্থান নির্ণয় করতে গেলে পরস্পর লম্ব দুটি অক্ষ থেকে নির্দিষ্ট দিকে ওই বিন্দুর লম্ব দূরত্ব কত তা জানা দরকার এই ধারণাই গণিতে একটি বিশেষ শাখার মূল বিষয় গণিতের সেই শাখাটি হল স্থানাঙ্ক জ্যামিতি ( Coordinate Geometry ) . এই ধারণার জন্যেই দার্শনিক ও গণিতজ্ঞ রেনে দে' কার্তে ।
কার্তেজীয় পদ্ধতি ( Cartesian System )
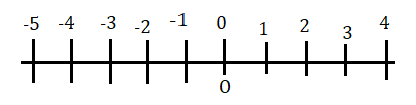
এই রেখার O হল মূলবিন্দু। O থেকে ধনাত্মক দিকে 4 এর দূরত্ব 4 একক এবং একই ভাবে O থেকে ঋণাত্মক দিকে 5 এর দূরত্ব -5 একক দে' কার্তে এইরকম দুটি সংখ্যা রেখার তলকে পরস্পর লম্বভাবে রেখে ওই তলের কোনো বিন্দুর অবস্থান নির্ণয়ের ধারণার জন্ম দিয়েছিলেন ।
স্থানাঙ্ক অক্ষ ও চারপদ
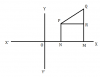
XOX' এবং YOY' সরলরেখা দুটি লম্বভাবে পরস্পরকে O বিন্দুতে ছেদ করেছে। XOX' রেখাটি অনুভূমিক ( Horizontal ) এবং YOY' রেখাটি উল্লম্ব ( Vertical ) . এই দুটি সরলরেখা হল প্রধান রেখা বা অক্ষরেখা ( principal axes ) . অনুভূমিক রেখাটি x অক্ষ ( x axis ) এবং উলম্ব রেখাটি হল y অক্ষ ( y axis ) । অক্ষ রেখাদ্বয়ের ছেদবিন্দু অর্থাৎ O কে মূলবিন্দু ( Origin ) বলে ।
O বিন্দু থেকে শুরু করে X অক্ষ বরাবর ডানদিকে ধনাত্মক ও বাঁদিকে ঋণাত্মক এবং Y অক্ষ বরাবর উপরদিকে ধনাত্মক ও নীচের দিক ঋণাত্মক । এই তলটিকে বলা হয় কার্তেজীয় তল বা স্থানাঙ্ক তল বা xy তল ।
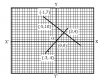
অক্ষরেখা দুটি লেখ কাগজকে চারভাগে বিভক্ত করেছে । এক একটি ভাগকে বলা হয় পাদ ( quadrant ) . ধনাত্মক X অক্ষ ও ধনাত্মক Y অক্ষ এর মাঝের অঞ্চলটিকে বলা হয় প্রথম পাদ ( 1st Quadrant ), ঋণাত্মক X অক্ষ ও ধনাত্মক Y অক্ষ এর মাঝের অঞ্চলটিকে বলা হয় দ্বিতীয় পাদ ( 2nd Quadrant ) , ঋণাত্মক X অক্ষ ও ঋণাত্মক Y ওখ এর মাঝের অঞ্চল টিকে বলা হয় তৃতীয় পাদ ( 3rd Quadrant ) এবং ধনাত্মক X অক্ষ ও ঋণাত্মক Y অক্ষ এর মাঝের অঞ্চলটিকে বলা হয় চতুর্থ পাদ ( 4th Quadrant ) ।
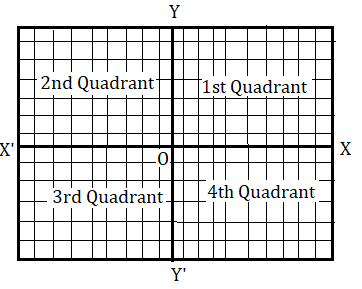
কোনো বিন্দুর x স্থানাঙ্ক বা ভুজ হল x অক্ষ বরাবর y অক্ষ থেকে ওই বিন্দুর চিহ্নসহ লম্ব দূরত্ব । 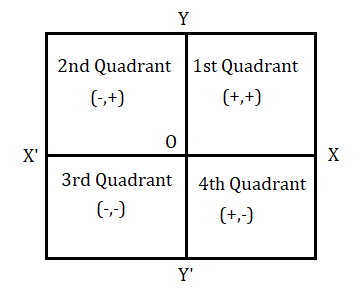
( x এর ধনাত্মক স্থানাঙ্কের ক্ষেত্রে মূলবিন্দু থেকে x অক্ষের ধনাত্মক দিক বরাবর এবং ঋণাত্মক স্থানাঙ্কের ক্ষেত্রে মূলবিন্দু থেকে x অক্ষের ঋণাত্মক দিক বরাবর মাপতে হয়। )
কোনো বিন্দুর y স্থানাঙ্ক বা কোটি হল y অক্ষ বরাবর x অক্ষ থেকে ওই বিন্দুর চিহ্নসহ লম্ব দূরত্ব।
( y এর ধনাত্মক স্থানাঙ্কের ক্ষেত্রে মূলবিন্দু থেকে y অক্ষের ধনাত্মক দিক বরাবর এবং ঋণাত্মক স্থানাঙ্কের ক্ষেত্রে মূলবিন্দু থেকে y অক্ষের ঋণাত্মক দিক বরাবর মাপতে হয়। )
স্থানাঙ্কের তলে কোনো বিন্দুর স্থানাঙ্ক নির্দিষ্টভাবে নির্দেশ করার সময় ( x স্থানাঙ্ক , y স্থানাঙ্ক ) এইভাবে লেখা হয়। যেমন A বিন্দুর স্থানাঙ্ক (4,6) এবং মূলবিন্দুর স্থানাঙ্ক (0,0) .
কোনো বিন্দুর অবস্থান ছক কাগজের XOX' ও YOY' দুটি লম্ব অক্ষ থেকে কত হবে তার নির্ণয়
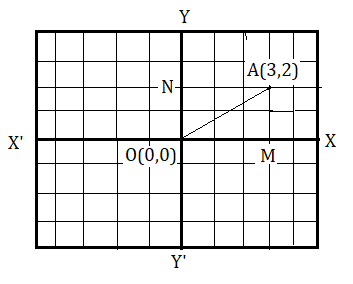 প্রথমে ছক কাগজের ক্ষুদ্রত্তম বর্গক্ষেত্রের একটি বাহুর দৈর্ঘ্য এক একক ধরলাম। এবার A থেকে y অক্ষের উপর AN লম্ব টানলাম। এরপর A থেকে x অক্ষের ওপর AM টানলাম। দেখা গেল y অক্ষ থেকে x অক্ষের ধনাত্মক দিকে A বিন্দুর লম্ব দূরত্ব NA = MO = 3 একক এবং x অক্ষ থেকে y অক্ষের ধনাত্মক দিকে A বিন্দুর লম্ব দূরত্ব MA = ON = 2 একক। অর্থাৎ A বিন্দুর ভুজ হল 3 এবং কোটি হল 2 . অতএব A বিন্দুর স্থানাঙ্ক (3,2) .
প্রথমে ছক কাগজের ক্ষুদ্রত্তম বর্গক্ষেত্রের একটি বাহুর দৈর্ঘ্য এক একক ধরলাম। এবার A থেকে y অক্ষের উপর AN লম্ব টানলাম। এরপর A থেকে x অক্ষের ওপর AM টানলাম। দেখা গেল y অক্ষ থেকে x অক্ষের ধনাত্মক দিকে A বিন্দুর লম্ব দূরত্ব NA = MO = 3 একক এবং x অক্ষ থেকে y অক্ষের ধনাত্মক দিকে A বিন্দুর লম্ব দূরত্ব MA = ON = 2 একক। অর্থাৎ A বিন্দুর ভুজ হল 3 এবং কোটি হল 2 . অতএব A বিন্দুর স্থানাঙ্ক (3,2) .
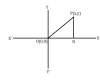
কীভাবে লেখচিত্রের মাধ্যমে একটি বিন্দু A(3,2) এর অবস্থান নির্ণয় করা হয়।
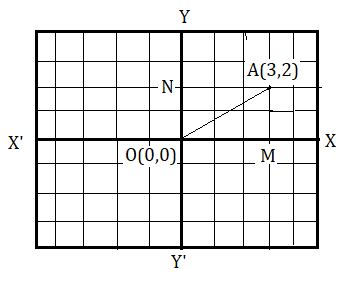 প্রথমে ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের একটি বাহুর দৈর্ঘ্য 1 একক ধরলাম । এখানে আমাদের A বিন্দুর অবস্থান নির্ণয় করতে হবে যার স্থানাঙ্ক হল (3,2) অর্থাৎ A বিন্দুর ভুজ হল 3 এবং কোটি হল 2 . এখন মূলবিন্দু O থেকে x অক্ষের ধনাত্মক দিক অর্থাৎ OX বরাবর 3 একক দূরত্ব অর্থাৎ M বিন্দুতে এগিয়ে গেলাম। তারপর M বিন্দু থেকে y অক্ষের ধনাত্মক দিক অর্থাৎ OY বরাবর 2 একক দূরত্ব এগিয়ে গেলাম যা হল A(3,2) বিন্দুর স্থানাঙ্ক। অনুরূপভাবে আগে y অক্ষ ও পরে x অক্ষ ধরে করলেও হয় ।
প্রথমে ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের একটি বাহুর দৈর্ঘ্য 1 একক ধরলাম । এখানে আমাদের A বিন্দুর অবস্থান নির্ণয় করতে হবে যার স্থানাঙ্ক হল (3,2) অর্থাৎ A বিন্দুর ভুজ হল 3 এবং কোটি হল 2 . এখন মূলবিন্দু O থেকে x অক্ষের ধনাত্মক দিক অর্থাৎ OX বরাবর 3 একক দূরত্ব অর্থাৎ M বিন্দুতে এগিয়ে গেলাম। তারপর M বিন্দু থেকে y অক্ষের ধনাত্মক দিক অর্থাৎ OY বরাবর 2 একক দূরত্ব এগিয়ে গেলাম যা হল A(3,2) বিন্দুর স্থানাঙ্ক। অনুরূপভাবে আগে y অক্ষ ও পরে x অক্ষ ধরে করলেও হয় ।
x অক্ষের উপরিস্থিত যেকোনো বিন্দুর x অক্ষ থেকে দূরত্ব 0 একক। সুতরাং x অবস্থিত কোনো বিন্দুর y স্থানাঙ্ক 0 . x অক্ষে অবস্থিত কোনো বিন্দুর স্থানাঙ্ক (x,0)
y অক্ষের উপরিস্থিত যেকোনো বিন্দুর y অক্ষ থেকে দূরত্ব 0 একক। সুতরাং y অবস্থিত কোনো বিন্দুর y স্থানাঙ্ক 0 . y অক্ষে অবস্থিত কোনো বিন্দুর স্থানাঙ্ক (y,0)
x অক্ষের ধনাত্মক দিকে x অক্ষের উপর কোনো বিন্দু অবস্থিত হলে x > 0 এবং y = 0 ; আবার x অক্ষের ঋণাত্মক দিকে x অক্ষের ঋণাত্মক দিকে x অক্ষের উপরে অবস্থিত হলে x < 0 এবং y = 0 ; অনুরূপভাবে y অক্ষের ধনাত্মক দিকে y অক্ষের উপর কোনো বিন্দু অবস্থিত হলে y > 0 এবং x = 0 ; আবার y অক্ষের ঋণাত্মক দিকে y অক্ষের ঋণাত্মক দিকে y অক্ষের উপরে অবস্থিত হলে y < 0 এবং x = 0 .
একচল ও দুই চলবিশিষ্ট একঘাত সমীকরণের ধারণা এবং তাদের লেখচিত্র অঙ্কন
এতক্ষন আমরা লেখচিত্রের সাহায্যে একটি বিন্দুর স্থানাঙ্ক নির্ণয় কিংবা বিন্দুটির স্থানাঙ্ক অনুযায়ী লিখচিত্রে বিন্দুটির অবস্থান নির্ণয় করেছি । এবার আমরা একটি একচল বা দুই চলবিশিষ্ট একঘাত সমীকরণকে কিভাবে লেখচিত্রে অঙ্কন করা যায় তা নির্ণয় করব । এক চলবিশিষ্ট সরলরেখার ক্ষেত্রে x কিংবা y এর বিভিন্ন মানের জন্য কোটি অথবা ভুজ 0 হবে অর্থাৎ y এর স্থানাঙ্ক বা x এর স্থানাঙ্ক 0 হবে। এবার যেসব মান পাওয়া যাবে তার x ও y এর মান যথাক্রমে x স্থানাঙ্ক এবং y স্থানাঙ্ক ধরে প্রত্যেক জোড়া সমাধানের জন্য লেখচিত্রে একটি করে বিন্দু পাবো । এই বিন্দুগুলিকে স্কেল দিয়ে তাদের যোগ করলে যে রৈখিক সমাধান স্বরূপ পাওয়া যায় তাই হল উক্ত সমীকরণের লেখচিত্র ।
আবার দুই চলবিশিষ্ট একঘাত সমীকরণের ক্ষেত্রে x কিংবা যা যেকোনো একটি অজ্ঞাত রাশির আকারে সমীকরণটিকে প্রকাশ করতে হবে । তারপর x ( বা y ) এর মানের জন্য y ( বা x ) এর যেসব মান পাওয়া যায় তা নির্ণয় করতে হবে। এই x এবং y এর যেসকল মান উক্ত সমীকরণকে সিদ্ধ করে তাদেরকে সমীকরণের সমাধান বা বীজ বলে । যেসব সমাধান পেলাম তার x ও y এর মান যথাক্রমে x স্থানাঙ্ক এবং y স্থানাঙ্ক ধরে প্রত্যেক জোড়া সমাধানের জন্য লেখচিত্রে একটি করে বিন্দু পাবো । এই বিন্দুগুলিকে স্কেল দিয়ে তাদের যোগ করলে যে রৈখিক সমাধান স্বরূপ পাওয়া যায় তাই হল উক্ত সমীকরণের লেখচিত্র ।
2x + 3y =16 একটি দুই চলবিশিষ্ট একঘাত সমীকরণ। এখন লেখচিত্রে এটি প্রকাশ করতে হবে ।
এখন 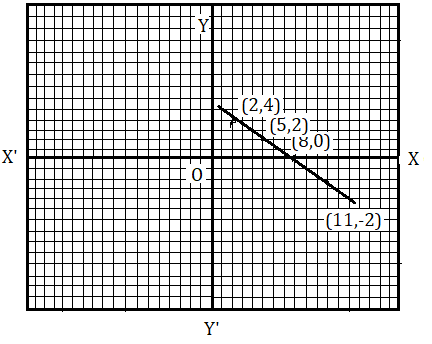
2x+3y=16⇒3y=16−2x⇒y=16−2x3
এখন x ও y এর যেসকল মান সমীকরণকে সিদ্ধ করে তাহল
| x | 8 | 5 | 2 | 11 |
| y=16−2x3 | 0 | 2 | 4 | -2 |
যেসব মান পেলাম তার x ও y এর মান যথাক্রমে x স্থানাঙ্ক ও y স্থানাঙ্ক ধরে প্রত্যেক জোড়া সমাধানের জন্য লেখচিত্রে একটি করে বিন্দু পাবো। এইসব বিন্দুগুলি হল (8,0) , (5,2) , (2,-4) এবং (11,2) . এই বিন্দুগুলিকে যোগ করলে একটি সরলরেখা পাওয়া যায়। এই সরলরেখার সমীকরণ হল 2x + 3y = 16 .
এক বা দুই চলবিশিষ্ট কোনো সমীকরণের লেখচিত্র একটি সরলরেখা হবে । রৈখিক সমীকরণের লেখচিত্র সর্বদা একটি সমতলে থাকে। এই সমতলটিকে কার্তেজীয় তল বলে। সুতরাং ax + by + c = 0 সমীকরণের লেখচিত্র একটি সরলরেখা । সমীকরণের লেখচিত্র যেহেতু একটি সরলরেখা সেই কারণে ধনাত্মক ও ঋণাত্মক দুই ধরণের স্থানাঙ্ক থাকবে ।
মনে রাখার বিষয়
- X অক্ষের সমীকরণ হল y = 0
- Y অক্ষের সমীকরণ হল x = 0
- X অক্ষের সমান্তরাল রেখার সমীকরণ y = k , যেখানে k হল constant , k≠0
- Y অক্ষের সমান্তরাল রেখার সমীকরণ x = k , যেখানে k হল constant , k≠0
- মূলবিন্দুর স্থানাঙ্ক ( 0 , 0 )
- যেকোনো একঘাত সমীকরণের ( যে সমীকরণে অজ্ঞাত রাশির সর্বোচ্চ ঘাত এক ) লেখ একটি সরলরেখা ।
- একটি সরলরেখার সাধারণ সমীকরণ ax+by+c=0
- ax+by=0 এই আকারের সমীকরণের লেখ মূলবিন্দু ( 0 , 0 ) দিয়ে যাবে ।
- দুটি সরলরেখা সমান্তরাল হওয়ার শর্ত হল x এর সহগ দুটির অনুপাত y এর সহগ দুটির অনুপাতের সমান হবে। অর্থাৎ a1x+b1y+c1=0 এবং a2x+b2y+c2=0 দুটি সরলরেখার সমীকরণ হলে তাদের সমান্তরাল হওয়ার শর্ত হল a1a2=b1b2⇒a1b2=a2b1 হবে। আর এটাই হল হল সমীকরণ দুটির সমাধানযোগ্য না হওয়ার শর্ত। কেননা সমীকরণদ্বয়ের লেখ কোনো বিন্দুতে পরস্পরকে ছেদ করেনা ।
- দুটি সরলরেখা পরস্পর লম্ব হওয়ার শর্ত x এর সহগ দুটির অনুপাত ও y এর সহগ দুটির ব্যাস্তানুপাতের মান সমান কিন্তু বিপরীত চিহ্ন যুক্ত। অর্থাৎ a1x+b1y+c1=0 এবং a2x+b2y+c2=0 দুটি সরলরেখার সমীকরণ হলে তাদের পরস্পরকে লম্ব হওয়ার শর্ত হল a1a2=−b2b1⇒a1b1=−a2b2⇒a1b1+a2b2=0 .
- xa+yb=1 আকারের সমীকরণ x অক্ষকে মূলবিন্দু থেকে ধনাত্মক দিকে a দূরত্ব এবং y অক্ষকে মূলবিন্দু থেকে ধনাত্মক দিকে b দূরত্বে ছেদ করে ।
- xa+yb=1 আকারের সমীকরণের লেখ অক্ষরেখাদ্বয়ের সঙ্গে যে ত্রিভুজ উৎপন্ন করে তার ক্ষেত্রফল হল 12ab বর্গ একক ।
- মূলবিন্দু O ( 0,0 ) থেকে P ( x,y ) বিন্দুর দূরত্ব হল √x2+y2
*****
- 32899 views