সান্তরিকের তৃতীয় উপপাদ্য (Parallelogram Theorem)
কোনো চতুর্ভুজের বিপরীত বাহুগুলি সমান হলে , চতুর্ভুজটি একটি সামন্তরিক হবে ।
প্রমাণ:
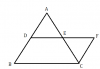
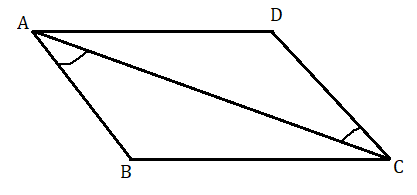 মনে করি ABCD একটি চতুর্ভুজ এর AB = DC এবং AD = BC
মনে করি ABCD একটি চতুর্ভুজ এর AB = DC এবং AD = BC
আমাদের প্রমাণ করতে হবে ABCD একটি সামন্তরিক
অঙ্কন : AC কর্ণ টানা হল
প্রমাণ : ত্রিভুজ ABC ও ত্রিভুজ ADC এর
AB = DC
BC = AD
এবং AC হল সাধারণ বাহু ।
অতএব ত্রিভুজ ABC ≅ ত্রিভুজ ADC
অতএব ∠BAC=∠ACD কিন্তু এরা একান্তর কোণ ।
অতএব AB ।। DC
আবার ∠ACB=∠CAD কিন্তু এরা একান্তর কোণ ।
অতএব AD ।। BC
অতএব ABCD হল সামান্তরিক ।
প্রয়োগ : ABCD আয়তক্ষেত্রের AB , BC , CD ও DA বাহুগুলির উপরে যথাক্রমে E , F , G , H বিন্দুগুলি এমনভাবে অবস্থিত যে AE = CG এবং BF = DH , যুক্তি দিয়ে প্রমাণ করতে হবে যে EFGH একটি সামন্তরিক ।
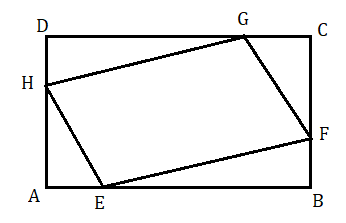 মনে করি ABCD আয়তক্ষেত্রের AE = CG এবং BF = DH
মনে করি ABCD আয়তক্ষেত্রের AE = CG এবং BF = DH
প্রমাণ করতে হবে যে EFGH একটি সামন্তরিক।
প্রমাণ : যেহেতু AD = BC এবং DH = BF
সুতরাং AD - DH = BC - BF
অতএব AH = CF
ত্রিভুজ AEH এবং ত্রিভুজ CGF এর
AH = CF
AE = CG
এবং ∠HAB=∠FCG=90∘
অতএব ত্রিভুজ AEH ≅ ত্রিভুজ CGF
সুতরাং EH = FG ( যেহেতু সর্বসম ত্রিভুজের অনুরূপ বাহু )
অনুরূপে প্রমাণ করা যায় EF = HG
যেহেতু EFGH চতুর্ভুজের EH = FG এবং EF = HG অর্থাৎ দুটি বিপরীত বাহুগুলি পরস্পর সমান ।
অতএব EFGH চতুর্ভুজটি একটি সামন্তরিক ।
*****