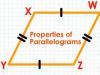
সামন্তরিকের ধর্ম (Properties of Parallelogram)
আমরা বিভিন্ন রকম চতুর্ভুজের আকার সম্পর্কে জেনেছি । যেমন বর্গক্ষেত্র , আয়তক্ষেত্র , রম্বস , কাইট , সামন্তরিক ও ট্রাপিজিয়াম। আবার কোনো চতুর্ভুজকে এই সমস্ত চতুর্ভুজের আকারে মধ্যে আনা সম্ভব হয়না । তাদেরকে চতুর্ভুজ নাম দেওয়া হয়েছে। এই অধ্যায়ে আমরা সামন্তরিকের ধর্ম সম্পর্কে আলোচনা করব ।
সামন্তরিক ( Parallelogram ) : যে চতুর্ভুজের বিপরীত বাহুগুলি পরস্পর সমান্তরাল তাকে সামান্তরিক বলে ।

উপরে চিত্র গুলি সবগুলি সামন্তরিক । এদের প্রত্যেকের বিপরীত বাহুগুলি পরস্পর সমান্তরাল ।
যে সামন্তরিকের একটি কোণ সমকোণ তাকে আয়তক্ষেত্র বলে ।
যে আয়তক্ষেত্রের একজোড়া সন্নিহিত বাহুর দৈর্ঘ্য সমান হলে তাকে বর্গক্ষেত্র বলে ।
যে সামন্তরিকের একজোড়া সন্নিহিত বাহুর দৈর্ঘ্য সমান হলে তাকে রম্বস বলে ।
আবার রম্বসের একটি কোণ সমকোণ হলে বর্গক্ষেত্র বলে ।
সুতরাং বর্গক্ষেত্র , আয়তক্ষেত্র , রম্বস এই সবই হল সামন্তরিক ।
সামন্তরিকের উপপাদ্য (Parallelogram Theorem)
প্রথম উপপাদ্য : কোনো চতুর্ভুজের একজোড়া বিপরীত বাহু সমান এবং সমান্তরাল হলে অপর জোড়া বিপরীত বাহুও সমান এবং সমান্তরাল হবে অর্থাৎ চতুর্ভুজটি একটি সামন্তরিক হবে। [ প্রমাণ ]
দ্বিতীয় উপপাদ্য : কোনো সামন্তরিকের (i) প্রতিটি কর্ণ সামন্তরিককে দুটি সর্বসম ত্রিভুজে বিভক্ত করে , (ii) বিপরীত বাহুগুলির দৈর্ঘ্য সামন। , (iii) বিপরীত কোণ গুলি মানে সমান। [ প্রমাণ ]
তৃতীয় উপপাদ্য : কোনো চতুর্ভুজের বিপরীত বাহুগুলি সমান হলে , চতুর্ভুজটি একটি সামন্তরিক হবে। [ প্রমাণ ]
চতুর্থ উপপাদ্য : কোনো চতুর্ভুজের বিপরীত কোণগুলি সমান হলে , চতুর্ভুজটি একটি সামন্তরিক হবে। [ প্রমাণ ]
পঞ্চম উপপাদ্য : সামন্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে। [ প্রমাণ ]
ষষ্ঠ উপপাদ্য : কোনো চতুর্ভুজের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করলে চতুর্ভুজটিকে সামন্তরিক বলে। [ প্রমাণ ]
*****