সামন্তরিকের দ্বিতীয় উপপাদ্য

সামন্তরিকের দ্বিতীয় উপপাদ্য (Parallelogram Theorem)

কোনো সামন্তরিকের 

(i) প্রতিটি কর্ণ সামন্তরিককে দুটি সর্বসম ত্রিভুজে বিভক্ত করে 

(ii) বিপরীত বাহুগুলির দৈর্ঘ্য সামন । 

(iii) বিপরীত কোণ গুলি মানে সমান । 

প্রমাণ:

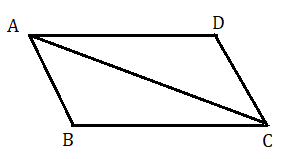
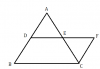
মনে করি ABCD একটি সামন্তরিক অর্থাৎ AD ।। BC এবং AB ।। DC . AC কর্ণ সামন্তরিককে ত্রিভুজ ABC এবং ত্রিভুজ ACD দুটি ত্রিভুজে বিভক্ত করেছে । প্রমাণ করতে হবে যে 

(i) ত্রিভুজ ABC  $\cong$ ত্রিভুজ ACD 

(ii) AB = DC এবং AD = BC

(iii) $\angle ABC = \angle ADC$ এবং $\angle BAD = \angle BCD$

প্রমাণ : ত্রিভুজ ABC এবং ত্রিভুজ ACD এর মধ্যে 

$\angle BAC =$একান্তর $\angle ACD$ ( যেহেতু AB ।। DC এবং AC হল ছেদক )

AC সাধারণ বাহু 

$\angle ACB =$ একান্তর $\angle CAD$ ( যেহেতু AD ।। BC এবং AC হল ছেদক )

অতএব ত্রিভুজ ABC $\cong$ ত্রিভুজ ADC 

অতএব AB = DC ও AD = BC ( সর্বসম ত্রিভুজের অনুরূপ বাহু )

আবার $\angle ABC = \angle ADC$ ( সর্বসম ত্রিভুজের অনুরূপ কোণ )

$\begin{array}{l} \angle BAC + \angle CAD = \angle ACB + \angle ACD\\  \Rightarrow \angle BAD = \angle BCD \end{array}$

*****