সামন্তরিকের পঞ্চম উপপাদ্য (Parallelogram Theorem)
সামন্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে।
প্রমাণ:
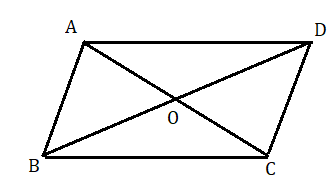 মনে করি ABCD একটি সামন্তরিক। এখানে AB ।। DC এবং AD ।। BC . AC এবং BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করেছে।
মনে করি ABCD একটি সামন্তরিক। এখানে AB ।। DC এবং AD ।। BC . AC এবং BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করেছে।
আমাদের প্রমাণ করতে হবে AO = CO এবং BO = DO
প্রমাণ : ত্রিভুজ AOB এবং ত্রিভুজ COD এর
AB = DC
∠ABO=∠CDO যেহেতু এরা একান্তর কোণ
∠BAO=∠DCO যেহেতু এরা একান্তর কোণ
অতএব ত্রিভুজ AOB ≅ ত্রিভুজ COD
অতএব AO = CO ( সর্বসম ত্রিভুজের অনুরূপ বাহু )
এবং BO = OD ( সর্বসম ত্রিভুজের অনুরূপ বাহু )
অর্থাৎ O হল AC এবং BD কর্ণদ্বয়ের মধ্যবিন্দু।
প্রয়োগ : রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখন্ডিত করে।
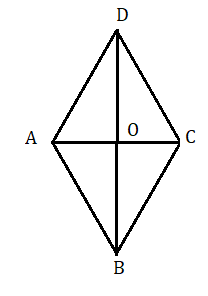 মনে করি ABCD একটি রম্বস এর AC এবং BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করেছে।
মনে করি ABCD একটি রম্বস এর AC এবং BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করেছে।
আমাদের প্রমাণ করতে হবে AO = CO , BO = DO এবং ∠AOB=90∘
প্রমাণ : যেহেতু রম্বস একটি সামন্তরিক সুতরাং তার কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করবে।
অর্থাৎ AO = CO এবং BO = DO হবে।
ত্রিভুজ AOB এবং ত্রিভুজ BOC এর
AB = BC
OB সাধারণ বাহু
AO = CO
অতএব ত্রিভুজ AOB ≅ ত্রিভুজ BOC
অতএব ∠AOB=∠BOC
এখন
∠AOB+∠BOC=180∘⇒2∠AOB=180∘⇒∠AOB=90∘
অতএব রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখন্ডিত করে।
ABCD সামন্তরিকের ∠BAD ও ∠BCD কোণের সমদ্বিখণ্ডক দুটি DC এবং AB বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে PAQC একটি সামন্তরিক।
 ABCD সামন্তরিকের ∠BAD ও ∠BCD কোণের সমদ্বিখণ্ডক দুটি DC এবং AB বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে।
ABCD সামন্তরিকের ∠BAD ও ∠BCD কোণের সমদ্বিখণ্ডক দুটি DC এবং AB বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে PAQC একটি সামন্তরিক।
প্রমাণ : ABCD সামান্তরিকের DC ।। AB এবং AP হল ছেদক।
সুতরাং ∠DPA=একান্তর ∠PAQ
আবার ∠PAQ=12∠DAB
⇒∠PAQ=12∠DCB ( যেহেতু ∠DAB=∠DCB )
⇒∠PAQ=∠PCQ ( যেহেতু 12∠DCB=∠PCQ )
⇒∠DPA=∠PCQ
কিন্তু ∠DPA ও ∠PCQ হল অনুরূপ কোন এবং DC হল ছেদক।
অতএব PA ।। CQ
আবার AQ ।। PC ( যেহেতু সামান্তরিকের বিপরীত বাহু AB ।। DC )
APCQ চতুর্ভুজের PA ।। CQ ও AQ ।। PC .
সুতরাং APCQ একটি সামন্তরিক।
প্রমাণ করতে হবে যে দুটি সমান্তরাল সরলরেখা ও তাদের একটি ছেদকের অন্তর্ভুক্ত অন্তঃকোণ গুলির সমদ্বিখন্ডকগুলি একটি আয়তকার চিত্র উৎপন্ন করে।
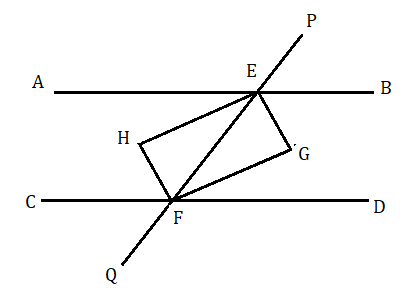 মনে করি AB ও CD দুটি সমান্তরাল সরলরেখাকে PQ ছেদক যথাক্রমে E ও F বিন্দুতে ছেদ করেছে। EG ও EH যথাক্রমে ∠BEF ও ∠AEF কোণ দুটিকে এবং FG ও FH যথাক্রমে ∠DFE ও ∠CFE কোণ দুটিকে সমদ্বিখন্ডিত করেছে।
মনে করি AB ও CD দুটি সমান্তরাল সরলরেখাকে PQ ছেদক যথাক্রমে E ও F বিন্দুতে ছেদ করেছে। EG ও EH যথাক্রমে ∠BEF ও ∠AEF কোণ দুটিকে এবং FG ও FH যথাক্রমে ∠DFE ও ∠CFE কোণ দুটিকে সমদ্বিখন্ডিত করেছে।
প্রমাণ করতে হবে EHFG একটি আয়তক্ষেত্র।
প্রমাণ : ∠AEF= একান্তর ∠EFD ( যেহেতু AB ।। CD এবং EF ছেদক )
সুতরাং , 12∠AEF=12∠EFD
অতএব ∠HEF=∠EFG কিন্তু এরা একান্তর কোণ।
অতএব HE ।। FG
অনুরূপে HF ।। GE
অতএব EHFG একটি সামন্তরিক ।
আবার ∠HEG=12(∠AEF+∠BEF)=12×2×90∘
অতএব ∠HEG=90∘
সুতরাং EHFG একটি আয়তক্ষেত্র ।
*****











