সামন্তরিকের প্রথম উপপাদ্য (Parallelogram Theorem)
কোনো চতুর্ভুজের একজোড়া বিপরীত বাহু সমান এবং সমান্তরাল হলে অপর জোড়া বিপরীত বাহুও সমান এবং সমান্তরাল হবে অর্থাৎ চতুর্ভুজটি একটি সামন্তরিক হবে ।
প্রমাণ:
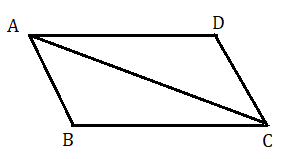
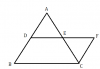
মনে করি ABCD একটি চতুর্ভুজ , এর AD = BC এবং AD ।। BC
আমাদের প্রমাণ করতে হবে
(i) AB = DC এবং AB ।। DC
(ii) ABCD একটি সামন্তরিক
অঙ্কন : AC কর্ণ টানলাম।
প্রমাণ : ত্রিভুজ ADC ও ত্রিভুজ ABC এর মধ্যে
AD = BC
AC সাধারণ বাহু
∠DAC= একান্তর ∠ACB ( যেহেতু AD ।। BC এবং AC হল ছেদক )
অতএব ত্রিভুজ ADC ≅ ত্রিভুজ ABC
AB = DC এবং ∠BAC=∠ACD কিন্তু এরা একান্তর কোণ ।
সুতরাং AB ।। DC
এখন ABCD চতুর্ভুজের AD ।। BC এবং AB ।। DC অর্থাৎ বিপরীত বাহু গুলি পরস্পর সমান্তরাল
সুতরাং ABCD চতুর্ভুজটি হল একটি সামন্তরিক ।
প্রয়োগ : PQRS সামন্তরিকের PS ও QR এর মধ্যবিন্দু হল যথাক্রমে A ও B . P , B ; Q , A ; R , A এবং B , S যোগ করা হল । PB ও QA পরস্পরকে C বিন্দুতে এবং RS ও RB পরস্পরকে D বিন্দুতে ছেদ করেছে । প্রমাণ করতে হবে যে (i) AQBS একটি সামন্তরিক , (ii) চতুর্ভুজ PBRA একটি সামন্তরিক , (iii) চতুর্ভুজ ACBD একটি সামন্তরিক ।
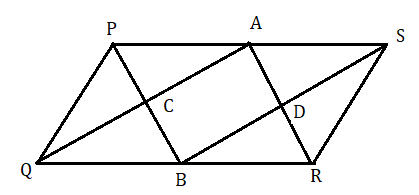 প্রমাণ : PQRS একটি সামন্তরিক। সুতরাং PS ।। QR এবং PS = QR
প্রমাণ : PQRS একটি সামন্তরিক। সুতরাং PS ।। QR এবং PS = QR
অতএব 12PS=12QR
সুতরাং PA = BR এবং AS = QB
অতএব AQBS চতুর্ভুজের AS ।। QB ( যেহেতু PS ।। QR )
এবং AS ।। QB
অতএব AQBS চতুর্ভুজটি একটি সামন্তরিক
একই ভাবে প্রমাণ করা যায় PBRA চতুর্ভুজটি একটি সামন্তরিক
ACBD চতুর্ভুজের AC ।। DB ( যেহেতু AQBS একটি সামন্তরিক )
BC ।। DA ( যেহেতু PBRA একটি সামন্তরিক )
অতএব ABCD একটি সামন্তরিক ।
*****