লেখচিত্রের সাহায্যে যেকোনো দুটি বিন্দুর মধ্যবর্তী দূরত্ব নির্ণয়
মনে করি P ও Q দুটি বিন্দু উহাদের স্থানাঙ্ক হল যথাক্রমে (x1,y1) এবং (x2,y2) . P ও Q যোগ করা হল এখন আমাদের PQ এর দূরত্ব বা দৈর্ঘ্য নির্ণয় করতে হবে । 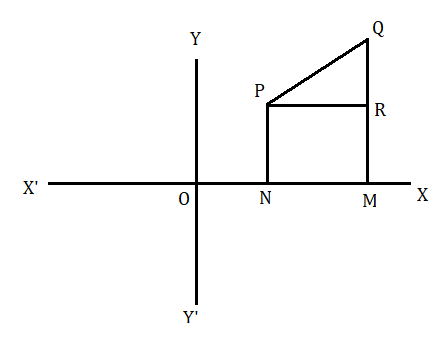
এখন P ও Q বিন্দু থেকে OX এর উপরে PN ও QM দুটি লম্ব অঙ্কন করা হল এবং P বিন্দু থেকে QM এর উপর PR লম্ব টানা হল ।
এখন PR ।। OX ( যেহেতু PR এবং OX দুটোই QM এর লম্ব )
অতএব PNMR একটি আয়তক্ষেত্র ।
অতএব PR = NM = OM - ON = x2−x1 ( যেহেতু ON=x1 এবং OM=x2 )
QR = QM - RM = QM - PN = y2−y1 ( যেহেতু PN=y1 এবং QM=y2 )
এখন PQR হল সমকোণী ত্রিভুজ। অতএব পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই
PQ2=PR2+QR2⇒PQ=√PR2+QR2=√(x2−x1)2+(y2−y1)2
সুতরাং P(x1,y1) এবং Q(x2,y2) দুটি বিন্দুর মধ্যবর্তী দূরত্ব হল √(x2−x1)2+(y2−y1)2 একক। যেহেতু দূরত্ব কখনো ঋণাত্মক হয়না সেই কারণেই সবসময় ধনাত্মক মান ধরা হবে ।
*****