সামন্তরিকের চতুর্থ উপপাদ্য (Parallelogram Theorem)
কোনো চতুর্ভুজের বিপরীত কোণগুলি সমান হলে , চতুর্ভুজটি একটি সামন্তরিক হবে ।
প্রমাণ:
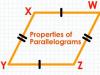
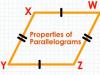
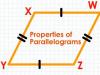
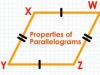
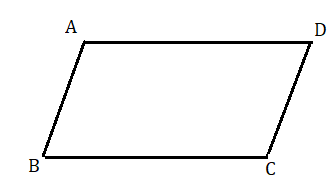 মনে করি ABCD চতুর্ভুজের ∠ABC=∠ADC এবং ∠BCD=∠DAB
মনে করি ABCD চতুর্ভুজের ∠ABC=∠ADC এবং ∠BCD=∠DAB
আমাদের প্রমাণ করতে হবে ABCD চতুর্ভুজটি একটি সামন্তরিক হবে।
প্রমাণ : যেহেতু চতুর্ভুজের চারটি কোণের যোগফল 360∘
অতএব ABCD চতুর্ভুজের
∠ABC+∠BCD+∠CDA+∠DAB=360∘⇒∠ABC+∠BCD+∠ABC+∠BCD=360∘
( যেহেতু ∠ABC=∠ADC এবং ∠BCD=∠DAB )
অতএব
2∠ABC+2∠BCD=360∘⇒2(∠ABC+∠BCD)=360∘⇒∠ABC+∠BCD=180∘
অতএব AB ।। DC ( যেহেতু BC ছেদকের একই পাশে অন্তঃস্থ কোণের যোগফল 180∘ )
আবার যেহেতু ∠ABC+∠BCD=180∘
∠ADC+∠BCD=180∘ ( যেহেতু ∠ABC=∠ADC )
এখানেও CD ছেদকের একই পাশে অন্তঃস্থ কোণের যোগফল 180∘
অতএব AD ।। BC
অতএব ABCD একটি সামন্তরিক।
প্রয়োগ : কোনো সামন্তরিকের চারটি কোণের সমদ্বিখণ্ডকগুলি পরস্পর মিলিত হয়ে একটি আয়তক্ষেত্র গঠন করবে।
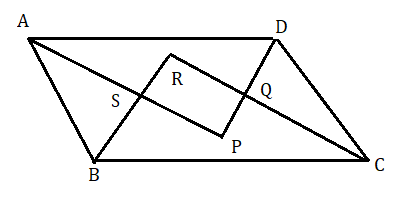 মনে করি ABCD একটি সামন্তরিকের ∠A,∠B,∠C এবং ∠D কোণের সমদ্বিখণ্ডক গুলি যথাক্রমে AP , BR , CR ও DP পরস্পর মিলিত হয়ে PQRS চতুর্ভুজ গঠন করেছে।
মনে করি ABCD একটি সামন্তরিকের ∠A,∠B,∠C এবং ∠D কোণের সমদ্বিখণ্ডক গুলি যথাক্রমে AP , BR , CR ও DP পরস্পর মিলিত হয়ে PQRS চতুর্ভুজ গঠন করেছে।
আমাদের প্রমাণ করতে হবে PQRS চতুর্ভুজটি হল একটি আয়তক্ষেত্র
প্রমাণ : ABCD সামন্তরিকের AB ।। DC এবং AD হল ভেদক
অতএব
∠BAD+∠ADC=180∘⇒12∠BAD+12∠ADC=12×180∘⇒∠PAD+∠PDA=90∘
সুতরাং ত্রিভুজ APD এর ∠PAD+∠PDA=90∘
অতএব ∠APD=180∘−90∘=90∘
অনুরূপে প্রমাণ করা যায় ∠BRC=90∘,∠ASB=90∘=∠RSP এবং ∠CQD=90∘=∠RQP
অতএব PQRS চতুর্ভুজের ∠PSR=∠PQR=90∘ এবং ∠SRQ=∠SPQ=90∘
যেহেতু PQRS চতুর্ভুজের বিপরীত বাহুগুলি সমান , সুতরাং PQRS চতুর্ভুজটি হল একটি সামন্তরিক ।
আবার PQRS সামন্তরিকের প্রত্যেকটি কোণের মান 90∘ , সুতরাং PQRS সামন্তরিকটি হল একটি আয়তক্ষেত্র ।
*****