News/ Events/ Current Affairs
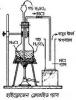
হাইড্রোজেন ক্লোরাইড এবং হাইড্রোক্লোরিক অ্যাসিড
পুষ্টি, পুষ্টির পর্যায় ও পুষ্টির প্রয়োজনীয়তা
Problem 0014 | Quadratic Equation
উদাহরন ১৪৷ যদি [tex]{x^2} + bx + ca = 0[/tex] এবং [tex]{x^2} + cx + ab = 0[/tex] সমীকরণ দুটির শূন্য নয় এমন একটিমাত্র সাধারণ বীজ থাকে তবে প্রমান করো যে, তাদের অন্য বীজগুলি [tex]{t^2} + at + bc = 0[/tex] সমীকরণকে সিদ্ধ করবে। [Jt. Ent.
- Read more about Problem 0014 | Quadratic Equation
- Log in or register to post comments
- 32 views
Problem 0013 | Quadratic Equations
উদাহরণ ১৩৷ (১) k এর যে সব মানের জন্য [tex]{x^2} - kx - 21 = 0[/tex] এবং [tex]{x^2} - 3kx + 35 = 0[/tex] সমীকরণ দুটির একটি সাধারণ বীজ থাকবে তা নির্ণয় কর। [H.S ‘87]
- Read more about Problem 0013 | Quadratic Equations
- Log in or register to post comments
- 27 views
Problem 0012 | Quadratic Equation
উদাহরণ ১২৷ [tex]a,b,c[/tex] বাস্তব হলে প্রমান করো যে , [tex]\frac{1}{{x - a}} + \frac{1}{{x - b}} + \frac{1}{{x - c}} = 0[/tex] সমীকরণের বীজগুলি সর্বদা বাস্তব এবং [tex]a = b = c[/tex] না হলে বীজ দুটি সমান হতে পারে না। [Jt. Ent. ‘86]
সমাধানঃ সমীকরণটি হল
- Read more about Problem 0012 | Quadratic Equation
- Log in or register to post comments
- 14 views
Problem 0011 | Quadratic Equations
উদাহরণ ১১৷ দেখাও যে [tex]a\left( {b - c} \right){x^2} + b\left( {c - a} \right)x + c\left( {a - b} \right) = 0[/tex] সমীকরণের বীজ দুটি সমান হলে [tex]\frac{1}{a},\frac{1}{b},\frac{1}{c}[/tex] সামান্তর প্রগতিতে থাকবে। [H.S ‘96]
সমাধানঃ
মনে করি
- Read more about Problem 0011 | Quadratic Equations
- Log in or register to post comments
- 24 views
Problem 0010 | Quadratic Equations
উদাহরণ ১০৷ [tex]p{x^2} - 2qx + p = 0[/tex] সমীকরণের বীজ দুটি বাস্তব ও অসমান হলে দেখাও যে, [tex]q{x^2} - 2px + q = 0[/tex] সমীকরণের বীজ দুটি কাল্পনিক হবে এবং বিপরীতক্রমেও তা সত্য ( p, q বাস্তব)
[H.S ‘93]
- Read more about Problem 0010 | Quadratic Equations
- Log in or register to post comments
- 6 views
Problem 009 | Quadratic Equations
উদাহরণ ৯৷ [tex]a,b,c[/tex] বাস্তব ও মূ্লদ এবং [tex]a + b + c = 0[/tex] হলে দেখাও যে, [tex]a{x^2} + bx + c = 0[/tex] দ্বিঘাত সমীকরণের বীজ দুটি মূলদ হবে। [H.S ‘98]
সমাধানঃ
- Read more about Problem 009 | Quadratic Equations
- Log in or register to post comments
- 9 views
তড়িৎ-বিশ্লেষণের প্রয়োগ
- Read more about তড়িৎ-বিশ্লেষণের প্রয়োগ
- 35642 views