Mathematics Syllabus for Class - IX Standard
নবম শ্রেণী - (Class- IX)
পাটি গণিত
১ . পূর্বপাঠের পূনরালোচনা । (Revision of Previous Lessons)
২. ত্রৈরাশিকের ব্যাপকতর প্রয়োগ ।
৩. সরল সুদকষা ।
৪. অংশীদারী কারবার ও তার বিভিন্ন সমস্যায় অনুপাত ও সমানুপাতের প্রয়োগ ।
৫. ব্যাঙ্কের বিভিন্ন সঞ্চয় প্রকল্পের সঙ্গে পরিচিতি । যেমন S.B.A/c, R.D. A/c, T.D. A/c, F.D. A/c, Bank Draft, Cheque ইত্যাদি ।
বীজগণিত
১. পূর্বপাঠের পূনরালোচনা ।
২. ভাগ প্রক্রিয়ার দ্বারা সহজ ক্ষেত্রে গ.সা,গু. নির্ণয় ।
৩. দুই অজ্ঞাত রাশির সহ-সমীকরণ গঠন , সমাধান , ( তুলনামূলক ও পরিবর্ত পদ্ধতিতে ) ও প্রয়োগ ।
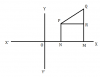
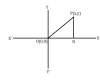
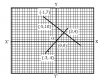
৪. কার্তেসীয় লম্ব স্থানাঙ্কের ধারনা । অক্ষের উপর দুইটি বিন্দুর দুরত্ব । লেখচিত্র ( দ্বিমাত্রিক) । এক্ঘাত দ্বিচল বিশিষ্ট সমীকরণের লেখচিত্র অঙ্কন । লেখচিত্রের সাহায্যে দুইচলবিশিষ্ট একঘাত সহসমীকরণের সমাধান ।
জ্যামিতি
১. পূর্বপাঠের পূনরালোচনা ।
২. নিম্নলিখিত প্রতিজ্ঞাগুলি প্রতিষ্ঠিত করা ।
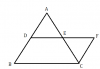
(ক) কোনো ত্রিভুজের এক বাহুর মধ্যবিন্দু দিয়ে অন্য একটি বাহুর সমান্তরাল সরল রেখা অঙ্কন করলে উহা তৃতীয় বাহুকে সমদ্বিখন্ন্ডিত করে এবং ত্রিভুজের বাহুগুলির দ্বারা সমান্তরাল সরলরেখার খন্ন্ডিতাংশ দ্বিতীয় বাহুর অর্ধেকের সমান । কোনো ত্রিভুজের দুই বাহুর মধ্যবিন্দুর সংযোজক রেখাংশ তৃতীয় বাহুর অর্ধেক ও সমান্তরাল ।
(খ) যদি তিনটি বা তার বেশি সমান্তরাল সরলরেখা যে-কোনো একটি ভেদক থেকে সমান সমান অংশ খন্ডিত করে , তাহলে তারা অপর যে কোনো ভেদক থেকেও সমান সমান অংশ খন্ডিত করবে ।
(গ) (i) যে সকল সামন্তরিক একই ভূমি ও একই সমান্তরালযুগলের ( অর্থাৎ একই উচ্চতা বিশিষ্ট ) মধ্যে অবস্থিত , তাদের ক্ষেত্রফল সমান ।
(ii) একই ভূমি (অথবা সমান সমান ভূমি ) এবং একই সমান্তরালযুগলের মধ্যে (অর্থাৎ একই উচ্চতা বিশিষ্ট) অবস্থিত ত্রিভুজগুলির ক্ষেত্রফল সমান ।
(iii) দুইটি সমান ক্ষেত্রফল বিশিষ্ট ত্রিভুজের একই ভূমির উপর অবস্থিত এবং উহার একই দিকে অবস্থিত হলে তারা একই সমান্তরালযুগলের মধ্যে অবস্থিত ।
(iv) কোনো ত্রিভুজ ও কোনো সামান্তরিক একই ভূমি ও একই সমান্তরালযুগলের মধ্যে অবস্থিত হলে , ত্রিভুজের ক্ষেত্রফল সামান্তরিকের ক্ষেত্রফলের অর্ধেক হবে ।
(ঘ) (i) যেকোনো ত্রিভুজের বাহুগুলির লম্ব সমদ্বিখন্ডক তিনটি সমবিন্দু ।
(ii) যেকোনো ত্রিভুজের শীর্ষ বিন্দু থেকে বিপরীত বাহুগুলির উপর অঙ্কিত লম্ব তিনটি সমবিন্দু ।
(iii) যেকোনো ত্রিভুজের কোণগুলির অন্তর্সমদ্বিখন্ডিত তিনটি সমবিন্দু ।
(iv) যেকোনো ত্রিভুজের মধ্যমা তিনটি সমবিন্দু ।
৩. পিথাগোরাসের উপপাদ্য : বিবৃতি ও প্রয়োগ ।
৪. অঙ্কন :
(i) একটি নির্দিষ্ট ত্রিভুজের সমান ক্ষেত্রফলবিশিষ্ট একটি সামান্তরিক অঙ্কন করতে হবে , যার একটি কোণ নির্দিষ্ট কোণের সমান ।
(ii) একটি চতুর্ভুজের সমান ক্ষেত্রফলবিশিষ্ট একটি ত্রিভুজ অঙ্কন করতে হবে ।
পরিমিতি
১. আয়াতক্ষেত্র, বর্গক্ষেত্র, ত্রিভুজের পরিসীমা ও ক্ষেত্রফল এবং যে-কোনো ঋজুরেখ ক্ষেত্রের ক্ষেত্রফল ।
২. বৃত্তের পরিধি ও ক্ষেত্রফল ([tex]\pi[/tex]-এর আসন্ন মান [tex]{{22} \over 7}[/tex] নেওয়া হবে ।
( কেবল মাত্র সূত্রের বিবৃতি ও তাদের সাংখ্যমানের প্রয়োগ ।
৩. সমকোণী চৌপল : তল এবং আয়তন সংক্রান্ত সমস্যাবলি ।
*****