সামন্তরিকের ষষ্ঠ উপপাদ্য (Parallelogram Theorem)
কোনো চতুর্ভুজের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করলে চতুর্ভুজটিকে সামন্তরিক বলে ।
প্রমাণ:
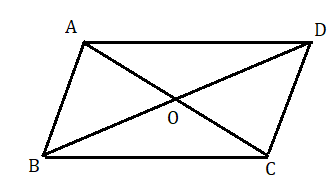 মনে করি ABCD চতুর্ভুজের O হল AC ও BD কর্ণের মধ্যবিন্দু ।
মনে করি ABCD চতুর্ভুজের O হল AC ও BD কর্ণের মধ্যবিন্দু ।
অর্থাৎ AO = CO এবং BO = DO
আমাদের প্রমাণ করতে হবে ABCD একটি সামান্তরিক ।
প্রমাণ : ত্রিভুজ AOB এবং ত্রিভুজ COD এর
AO = CO
BO = DO
[tex]\angle AOB[/tex] = বিপ্রতীপ কোণ [tex]\angle DOC[/tex]
অতএব ত্রিভুজ AOB [tex] \cong [/tex] ত্রিভুজ COD
অতএব AB = DC ( এরা সর্বসম ত্রিভুজের অনুরূপ বাহু )
[tex]\angle BAO = \angle DCO[/tex] কিন্তু এরা একান্তর কোণ
অতএব AB ।। DC
অর্থাৎ চতুর্ভুজটির একজোড়া বিপরীত বাহু সমান এবং সমান্তরাল ।
অতএব অপর জোড়া বিপরীত বাহুও সমান এবং সমান্তরাল হবে ।
অতএব ABCD একটি সামন্তরিক।
প্রয়োগ : ABCD একটি সামন্তরিকের AC ও BD কর্ণ দুটি O বিন্দুতে মিলিত হয়েছে । AC কর্ণের উপর P ও R দুটি এমন বিন্দু যাতে AP = CR হয়। প্রমাণ করতে হবে চতুর্ভুজ PBRD একটি সামন্তরিক ।
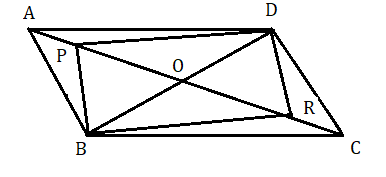 ABCD একটি সামন্তরিকের AC ও BD কর্ণ দুটি O বিন্দুতে মিলিত হয়েছে। AC কর্ণের উপর P ও R দুটি এমন বিন্দু যাতে AP = CR হয় ।
ABCD একটি সামন্তরিকের AC ও BD কর্ণ দুটি O বিন্দুতে মিলিত হয়েছে। AC কর্ণের উপর P ও R দুটি এমন বিন্দু যাতে AP = CR হয় ।
আমাদের প্রমাণ করতে হবে চতুর্ভুজ PBRD একটি সামন্তরিক।
প্রমাণ : যেহেতু ABCD একটি সামন্তরিক , সুতরাং তার কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করবে ।
অর্থাৎ , OA = OC এবং OB = OD হবে ।
এখন OP =OA - AP
অতএব OP = OC - CR ( যেহেতু OA = OC এবং AP = CR )
অতএব OP = OR
সুতরাং PBRD চতুর্ভুজের OP = OR এবং OB = OD অর্থাৎ PBRD চতুর্ভুজের PR এবং BD দুটি কর্ণদ্বয় পরস্পরকে O বিন্দুতে সমদ্বিখন্ডিত করেছে ।
সুতরাং PBRD একটি সামন্তরিক ।
ABCD একটি সামন্তরিকের DA ও DC বাহুকে যথাক্রমে P ও Q বিন্দুতে এমন ভাবে বাড়ানো হল যাতে AP = DA এবং CQ = DC হয়। প্রমাণ করতে হবে যে P , B , Q তিনটি সমরেখ ।
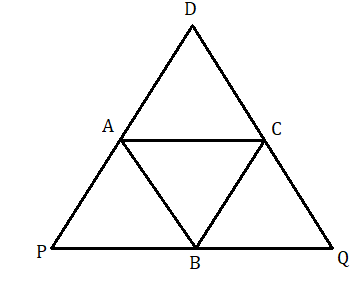
ABCD একটি সামান্তরিকের DA ও DC বাহুকে যথাক্রমে P ও Q বিন্দুতে এমন ভাবে বাড়ানো হল যাতে AP = DA এবং CQ = DC হয় ।
আমাদের প্রমাণ করতে হবে যে P , B , Q তিনটি সমরেখ ।
অঙ্কন : P , B ; B , Q এবং C , Q যুক্ত করলাম ।
প্রমাণ : যেহেতু ABCD একটি সামান্তরিক তাই DA = CB এবং DA ।। CB .
দেওয়া আছে AP = DA
অতএব AP = CB এবং AP ।। CB
অতএব চতুর্ভুজ APBC একটি সামন্তরিক ।
সুতরাং PB ।। AC ..........(i)
আবার ABCD একটি সামন্তরিক তাই DC = AB এবং DC ।। AB .
দেওয়া আছে CQ = DC
অতএব CQ = AB এবং CQ ।। AB
অতএব চতুর্ভুজ ABQC একটি সামন্তরিক ।
সুতরাং BQ ।। AC .............(ii)
(i) ও (ii) থেকে পাই
PB ।। BQ
আবার যেহেতু B বিন্দুটি দুটি সরলরেখাতেই আছে সুতরাং PB ও BQ একই সরলরেখাতেই আছে । সুতরাং P , B ও Q বিন্দু তিনটি সমরেখ ।
*****







