ভেদক ও মধ্যবিন্দু সংক্রান্ত উপপাদ্য (Transversal and Mid-Point Theorem)
উপপাদ্য 1: কোনো ত্রিভুজের দুটি বাহুর মধ্যবিন্দুদ্বয়ের সংযোগ সরলরেখাংশ তৃতীয় বাহুর সমান্তরাল ও অর্ধেক ।
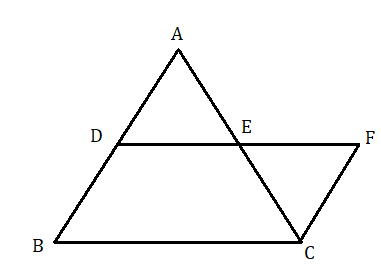 মনে করি ABC ত্রিভুজের AB বাহুর মধ্যবিন্দু হল D এবং AC বাহুর মধ্যবিন্দু হল E . DE যুক্ত করলাম ।
মনে করি ABC ত্রিভুজের AB বাহুর মধ্যবিন্দু হল D এবং AC বাহুর মধ্যবিন্দু হল E . DE যুক্ত করলাম ।
প্রমাণ করতে হবে (i) DE ।। BC এবং (ii) [tex]DE = \frac{1}{2}BC[/tex]
অঙ্কন : ED কে F বিন্দু পর্যন্ত এমন ভাবে বর্ধিত করা হল যাতে DE = EF হয়। B , F যুক্ত করলাম ।
প্রমাণ : ত্রিভুজ ADE এবং ত্রিভুজ EFC এর
DE = EF ( অঙ্কনানুযায়ী )
AE = EC ( শর্তানুযায়ী )
[tex]\angle AED = \angle CEF[/tex] ( বিপ্রতীপ কোণ )
অতএব ত্রিভুজ ADE [tex] \cong [/tex] ত্রিভুজ CEF .
অতএব AD = CF ( সর্বসম ত্রিভুজের অনুরূপ বাহু ).
আবার AD = BD .
সুতরাং CF = BD .
[tex]\angle DAE = \angle ECF[/tex] ( কিন্তু এরা একান্তর কোণ )
অতএব AD ।। CF অর্থাৎ BD ।। CF
অতএব BDFC চতুর্ভুজের BD ।। CF এবং CF = BD .
অতএব চতুর্ভুজ BDFC হল একটি সামান্তরিক।
অতএব DF ।। BC অর্থাৎ DE ।। BC ( প্রমাণিত )
আবার BDFC সামান্তরিকের DF = BC
E হল DF এর মধ্যবিন্দু ।
অতএব [tex]2DE = BC \Rightarrow DE = \frac{1}{2}BC[/tex] ( প্রমাণিত ) .
ABC সমবাহু ত্রিভুজের AB , BC ও AC বাহুর মধ্যবিন্দু হল যথাক্রমে P , Q ও R . প্রমাণ করতে হবে PQR একটি সমবাহু ত্রিভুজ ।
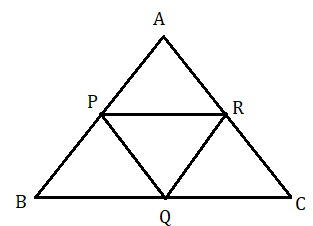 প্রমাণ : ত্রিভুজ ABC এর AB ও AC বাহুর মধ্যবিন্দু যথাক্রমে P ও R .
প্রমাণ : ত্রিভুজ ABC এর AB ও AC বাহুর মধ্যবিন্দু যথাক্রমে P ও R .
অতএব [tex]PR = \frac{1}{2}BC[/tex] ........(i)
একই ভাবে [tex]PQ = \frac{1}{2}AC[/tex].......(ii)
এবং [tex]QR = \frac{1}{2}AB[/tex].........(iii)
যেহেতু ABC একটি সমবাহু ত্রিভুজ
অতএব [tex]AB = BC = AC \Rightarrow \frac{1}{2}AB = \frac{1}{2}BC = \frac{1}{2}AC[/tex]
অতএব (iii) , (i) ও (ii) থেকে পাই
[tex]QR = PR = PQ[/tex]
অতএব PQR একটি সমবাহু ত্রিভুজ ।
ABCD ট্রাপিজিয়ামের দুটি তির্যক বাহু AD ও BC এর মধ্যবিন্দু যথাক্রমে E ও F . প্রমাণ করতে হবে EF ।। AB এবং [tex]EF = \frac{1}{2}\left( {AB + DC} \right)[/tex]
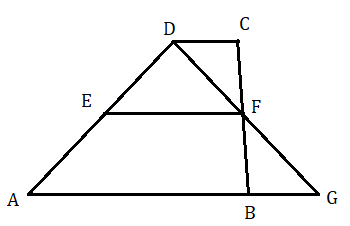 ABCD ট্রাপিজিয়ামের দুটি তির্যক বাহু AD ও BC এর মধ্যবিন্দু যথাক্রমে E ও F .
ABCD ট্রাপিজিয়ামের দুটি তির্যক বাহু AD ও BC এর মধ্যবিন্দু যথাক্রমে E ও F .
প্রমাণ করতে হবে EF ।। AB এবং [tex]EF = \frac{1}{2}\left( {AB + DC} \right)[/tex]
অঙ্কন : D , F যুক্ত করে এমন ভাবে বর্ধিত করলাম যা বর্ধিত AB বাহুকে G বিন্দুতে ছেদ করে।
প্রমাণ : ত্রিভুজ DCF ও ত্রিভুজ BFG এর মধ্যে
CF = BF ( F হল BC বাহুর মধ্যবিন্দু )
[tex]\angle DFC = \angle BFG[/tex] ( বিপ্রতীপ কোণ )
[tex]\angle DCF = \angle GBF[/tex] ( একান্তর কোণ )
অতএব ত্রিভুজ DCF [tex] \cong [/tex] ত্রিভুজ BFG
সুতরাং DF = FG ( সর্বসম ত্রিভুজের অনুরূপ বাহু ) অর্থাৎ F হল DG এর মধ্যবিন্দু ।
এখন ত্রিভুজ DGA এর E ও F হল যথাক্রমে AD ও DG এর মধ্যবিন্দু ।
অতএব EF ।। AG এবং [tex]EF = \frac{1}{2}AG[/tex]
এখন EF ।। AG অর্থাৎ EF ।। AB ( প্রমাণিত )
আবার
[tex]\begin{array}{l}
EF = \frac{1}{2}AG\\
\Rightarrow EF = \frac{1}{2}\left( {AB + BG} \right)\\
\Rightarrow EF = \frac{1}{2}\left( {AB + DC} \right)
\end{array}[/tex]
( যেহেতু DF = FG ) প্রমাণিত ।
প্রমাণ করতে হবে যে কোনো চতুর্ভুজের বাহুগুলির মধ্যবিন্দু পরপর যুক্ত করলে একটি সামান্তরিক পাওয়া যাবে ।
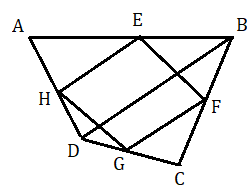 মনে করি ABCD একটি চতুর্ভুজ যার AB , BC , CD ও DA বাহুর মধ্যবিন্দু হল যথাক্রমে E , F , G ও H তাদের মধ্যবিন্দু। প্রমাণ করতে হবে EFGH হল একটি সামান্তরিক ।
মনে করি ABCD একটি চতুর্ভুজ যার AB , BC , CD ও DA বাহুর মধ্যবিন্দু হল যথাক্রমে E , F , G ও H তাদের মধ্যবিন্দু। প্রমাণ করতে হবে EFGH হল একটি সামান্তরিক ।
অঙ্কন : BD যুক্ত করা হল
প্রমাণ : ABD ত্রিভুজের AD ও AB এর মধ্যবিন্দু হল যথাক্রমে H ও E .
সুতরাং HE ।। BD এবং [tex]HE = \frac{1}{2}BD[/tex]..............(i)
আবার BCD ত্রিভুজের BC ও CD বাহুর মধ্যবিন্দু হল যথাক্রমে F ও G .
সুতরাং FG ।। BD এবং [tex]FG = \frac{1}{2}BD[/tex]..................(ii)
(i) ও (ii) থেকে পাই
HE ।। FG এবং [tex]HE = \frac{1}{2}BD = FG \Rightarrow HE = FG[/tex]
HEFG একটি সামান্তরিক। ( প্রমাণিত )
উপপাদ্য 2: কোনো ত্রিভুজের যে কোনো একটি বাহুর মধ্যবিন্দু দিয়ে অঙ্কিত দ্বিতীয় একটি বাহুর সমান্তরাল সরলরেখা তৃতীয় বাহুকে সমদ্বিখণ্ডিত করবে এবং ত্রিভুজের বাহুগুলির দ্বারা সমান্তরাল সরলরেখার খন্ডিতাংশ দ্বিতীয় বাহুর অর্ধেক হবে ।
 মনে করি ত্রিভুজ ABC এর AC বাহুর মধ্যবিন্দু E দিয়ে BC এর সমান্তরাল সরলরেখা টানা হল যা AB বাহুকে D বিন্দুতে ছেদ করে ।
মনে করি ত্রিভুজ ABC এর AC বাহুর মধ্যবিন্দু E দিয়ে BC এর সমান্তরাল সরলরেখা টানা হল যা AB বাহুকে D বিন্দুতে ছেদ করে ।
প্রমাণ করতে হবে (i) AD = BD এবং (ii) [tex]DE = \frac{1}{2}BC[/tex]
অঙ্কন : ED কে F বিন্দু পর্যন্ত এমন ভাবে বর্ধিত করা হল যাতে DE = EF হয়। B , F যুক্ত করলাম ।
প্রমাণ : ত্রিভুজ ADE এবং ত্রিভুজ EFC এর
AE = EC ( কল্পনানুসারে )
DE = EF ( অঙ্কনানুযায়ী )
[tex]\angle AED = \angle CEF[/tex] ( বিপ্রতীপ কোণ )
সুতরাং ত্রিভুজ ADE [tex] \cong [/tex] ত্রিভুজ EFC
অতএব AD = FC ( সর্বসম ত্রিভুজের অনুরূপ বাহু )
এবং [tex]\angle DAE = \angle FCE[/tex] ( কিন্তু এরা একান্তর কোণ )
অতএব AD ।। CF বা AB ।। CF
অর্থাৎ BD ।। CF আবার DF ।। BC
অতএব BDFC একটি সামন্তরিক ।
অতএব DF = BC এবং BD = CF
আবার AD = CF
অতএব BD = AD
এর থেকে বলা যায় D হল AB এর মধ্যবিন্দু। ( প্রমাণিত )
এখন
[tex]\begin{array}{l}
DF = BC\\
\Rightarrow DE + EF = BC\\
\Rightarrow DE + DE = BC\\
\Rightarrow 2DE = BC\\
\Rightarrow DE = \frac{1}{2}BC
\end{array}[/tex]
( প্রমাণিত )
বিকল্প পদ্ধতিতে প্রমাণ ত্রিভুজের যেকোনো দুটি বাহুর মধ্যবিন্দু দ্বয়ের সংযোগ সরলরেখা তৃতীয় বাহুর সমান্তরাল ও অর্ধেক হবে ।
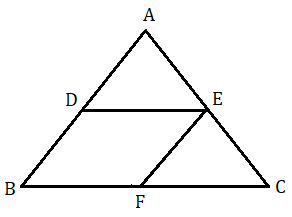 মনে করি ABC ত্রিভুজের AB ও AC বাহুর মধ্যবিন্দু দুটি যথাক্রমে D ও E . D , E যুক্ত করা হল।
মনে করি ABC ত্রিভুজের AB ও AC বাহুর মধ্যবিন্দু দুটি যথাক্রমে D ও E . D , E যুক্ত করা হল।
প্রমাণ করতে হবে যে (i) DE ।। BC এবং (ii) [tex]DE = \frac{1}{2}BC[/tex]
অঙ্কন : AC বাহুর মধ্যবিন্দু E দিয়ে AB বাহুর সমান্তরাল সরলরেখা টানলাম যা BC বাহুকে F বিন্দুতে ছেদ করে ।
প্রমাণ : E , AC বাহুর মধ্যবিন্দু এবং EF ।। AB ( অঙ্কনানুযায়ী )
অতএব F , BC এর মধ্যবিন্দু অর্থাৎ [tex]BF = \frac{1}{2}BC[/tex] এবং [tex]EF = \frac{1}{2}AB[/tex]
সুতরাং [tex]EF = \frac{1}{2}AB = DB[/tex] ( যেহেতু D , AB এর মধ্যবিন্দু )
চতুর্ভুজ DBEF এর
FE = DB এবং EF ।। DB ( অঙ্কনানুযায়ী )
অতএব DBEF একটি সামন্তরিক ।
সুতরাং DE ।। BF অর্থাৎ DE ।। BC ( প্রমাণিত )
[tex]DE = BF = \frac{1}{2}BC[/tex] ( প্রমাণিত )
ABC সমকোণী ত্রিভুজের অতিভুজ BC এর মধ্যবিন্দু D . প্রমাণ করতে হবে [tex]AD = \frac{1}{2}BC[/tex]
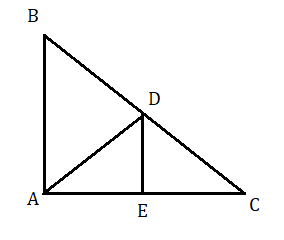 ত্রিভুজ ABC হল সমকোণী ত্রিভুজ । যার [tex]\angle A = {90^ \circ }[/tex] এবং D হল BC বাহুর মধ্যবিন্দু ।
ত্রিভুজ ABC হল সমকোণী ত্রিভুজ । যার [tex]\angle A = {90^ \circ }[/tex] এবং D হল BC বাহুর মধ্যবিন্দু ।
প্রমাণ করতে হবে [tex]AD = \frac{1}{2}BC[/tex]
অঙ্কন : D থেকে AB এর সমান্তরাল সরলরেখা টানলাম যা AC কে E বিন্দুতে ছেদ করেছে।
প্রমাণ : ত্রিভুজ ABC এর D হল BC বাহুর মধ্যবিন্দু এবং AD ।। DE ( অঙ্কনানুসারে ) ।
অতএব E হল AC এর মধ্যবিন্দু এবং [tex]DE = \frac{1}{2}AB[/tex]
এখন ত্রিভুজ ADE ও ত্রিভুজ CDE এর
AE = EC
ED হল সাধারণ বাহু ।
AB ।। ED এবং AC হল ভেদক অতএব [tex]\angle BAE = \angle DEC = {90^ \circ }[/tex]
অতএব [tex]\angle DEC = {90^ \circ }[/tex]
অতএব [tex]\angle DEA = \angle DEC[/tex]
অতএব ত্রিভুজ ADE [tex] \cong [/tex] ত্রিভুজ DEC
সুতরাং AD = DC
অতএব [tex]AD = DC = \frac{1}{2}BC[/tex]
ABC ত্রিভুজের AD মধ্যমার মধ্যবিন্দু E এবং বর্ধিত BE , AC বাহুকে F বিন্দুতে ছেদ করেছে প্রমাণ করতে হবে যে [tex]AF = \frac{1}{3}AC[/tex]
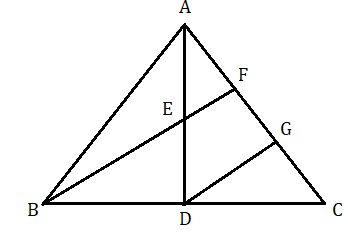 ABC ত্রিভুজের AD মধ্যমার মধ্যবিন্দু E এবং বর্ধিত BE , AC বাহুকে F বিন্দুতে ছেদ করেছে।
ABC ত্রিভুজের AD মধ্যমার মধ্যবিন্দু E এবং বর্ধিত BE , AC বাহুকে F বিন্দুতে ছেদ করেছে।
আমাদের প্রমাণ করতে হবে যে [tex]AF = \frac{1}{3}AC[/tex]
অঙ্কন : D বিন্দু দিয়ে BF এর সমান্তরাল সরলরেখা টানলাম যা AC বাহুকে G বিন্দুতে ছেদ করে।
প্রমাণ : ত্রিভুজ BFC এর BC বাহুর মধ্যবিন্দু হল D . [ যেহেতু AD হল মধ্যমা ]
এবং DG ।। BF ( অঙ্কনানুসারে )
অতএব G হল FC এর মধ্যবিন্দু।
সুতরাং FG = GC ...........(i)
এখন ADG ত্রিভুজের AD বাহুর মধ্যবিন্দু E এবং DG ।। EF ( অঙ্কনানুসারে )
অতএব F হল AG এর মধ্যবিন্দু।
সুতরাং AF = FG ............(ii)
(i) ও (ii) থেকে পাই
AF = FG = GC
সুতরাং [tex]AF = \frac{1}{3}AC[/tex]
ABCD সামান্তরিকের AB ও DC বাহুর মধ্যবিন্দুদ্বয় যথাক্রমে E এবং F ; A , F ও C , E যোগ করলাম যা BD কর্ণ কে যথাক্রমে P ও Q বিন্দুতে ছেদ করল। প্রমাণ করতে হবে যে AF ও CE , BD কর্ণকে সমত্রিখণ্ডিত করেছে ।
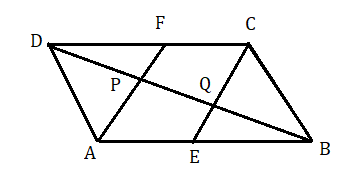 প্রমাণ : ABCD সামান্তরিকের AB ।। DC এবং AB = DC
প্রমাণ : ABCD সামান্তরিকের AB ।। DC এবং AB = DC
অতএব AE ।। FC এবং [tex]\frac{1}{2}AB = \frac{1}{2}DC[/tex]
অর্থাৎ AE = FC অতএব AECF একটি সামন্তরিক।
সুতরাং AF ।। EC
এখন ত্রিভুজ BAP এর E হল AB এর মধ্যবিন্দু এবং QE ।। PA
অতএব Q হল PB এর মধ্যবিন্দু।
সুতরাং BQ = QP ............(i)
আবার ত্রিভুজ DCQ এর F হল DC এর মধ্যবিন্দু এবং FP ।। CQ
অতএব P হল DQ এর মধ্যবিন্দু।
সুতরাং QP = PD ............(ii)
(i) এবং (ii) থেকে পাই
BQ = QP এবং QP = PD
অতএব BQ = PQ = PD .
তিন বা ততোধিক সমান্তরাল সরলরেখা কোনো একটি ভেদক থেকে সমান সমান অংশে খণ্ডিত করলে অপর যে কোনো ভেদক থেকেও সমান সমান অংশ খণ্ডিত করবে ।
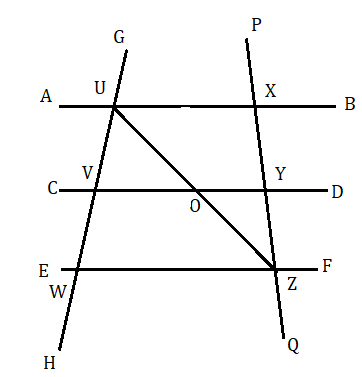
মনে করি AB , CD এবং EF তিনটি সমান্তরাল সরলরেখাকে GH ভেদক যথাক্রমে U , V এবং W বিন্দুতে ছেদ করে এবং UV = VW
আমাদের প্রমাণ করতে হবে যে আর একটি ভেদক PQ যদি AB , CD এবং EF তিনটি সমান্তরাল সরলরেখাকে যথাক্রমে X , Y এবং Z বিন্দুতে ছেদ করে তবে XY = YZ হবে ।
অঙ্কন : UZ যুক্ত করা হল। UZ সরলরেখা CD সরলরেখাকে O বিন্দুতে ছেদ করেছে ।
প্রমাণ : UWZ ত্রিভুজের VO ।। WZ এবং V হল UW এর মধ্যবিন্দু ।
অতএব O হল UZ এর মধ্যবিন্দু ।
আবার UXZ ত্রিভুজের UX ।। OY এবং O হল UZ এর মধ্যবিন্দু ।
অতএব Y হল XZ এর মধ্যবিন্দু অর্থাৎ XY = YZ ( প্রমাণিত ) ।
*****











