ক্ষেত্রফল সংক্রান্ত উপপাদ্য

ক্ষেত্রফল সংক্রান্ত উপপাদ্য (Theorems on Area)

ক্ষেত্রফল বলতে কি বোঝায় ?

ক্ষেত্রফল হল কোনো ক্ষেত্রের পরিমাপ ( Magnitude or measure ) . এই পরিমাপটি কোনো একক ( Unit ) সমেত প্রকাশ করা হয়। যেমন 50 বর্গ মিটার কোনো ক্ষেত্রের ক্ষেত্রফল । 

দুটি সমতলিক ক্ষেত্রের আকার ও মাপ যদি একই হয় তবে তাদের ক্ষেত্রফল একই রকম হয় । কিন্তু আবার দুটি সমতলিক ক্ষেত্রের আকার ও পরিমাপ ভিন্ন হলেও তাদের ক্ষেত্রফল একই রকম হতে পারে । যেমন 

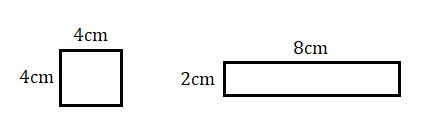
এখানে দুটি চিত্র দেওয়া আছে একটি বর্গাকার ও অন্যটি আয়তকার । বর্গাকার ক্ষেত্রের বাহুর দৈর্ঘ্য হল 4 সেমি ও আয়তকার ক্ষেত্রের বাহুর দৈর্ঘ্য ও প্রস্থ হল যথাক্রমে 2 সেমি ও 8 সেমি। কিন্তু তাদের প্রত্যেকের ক্ষেত্রফল হল 16 বর্গসেমি । 

 

কোনো সমতলিক ক্ষেত্রের ক্ষেত্রফলের ধর্ম 

1. A ও B দুটি সমতলিক ক্ষেত্র সর্বসম হলে A এর ক্ষেত্রফল = B এর ক্ষেত্রফল হবে । 
2. একটি সমতলিক ক্ষেত্রকে দুটি আলাদা আলাদা ( যদি একটি ক্ষেত্র অপরটির ক্ষেত্রের কোনও জায়গা না নেয় ) অংশ A ও B তে বিভুক্ত করলে ,

সমগ্র সমতলিক ক্ষেত্রের ক্ষেত্রফল = A অংশের ক্ষেত্রফল + B অংশের ক্ষেত্রফল

 ক্ষেত্রফল সংক্রান্ত উপপাদ্য ( Theorems of Area)

একই ভূমি এবং একই সমান্তরাল যুগলের মধ্যে অবস্থিত সামান্তরিকের ক্ষেত্রফল সমান 

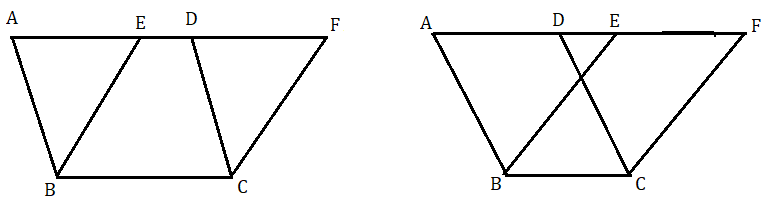
মনে করি ABCD ও EBCF দুটি সামান্তরিক একই ভূমি BC এবং একই সামান্তরিক যুগল AF ও BC এর মধ্যে অবস্থিত । 

আমাদের প্রমাণ করতে হবে যে ABCD ও EBCF সামান্তরিক দুটির ক্ষেত্রফল সমান । 

প্রমাণ : এখন ত্রিভুজ ABE ও ত্রিভুজ CDF এর 

AB = DC ( যেহেতু সামান্তরিকের বিপরীত বাহু )

BE = CF ( যেহেতু সামান্তরিকের বিপরীত বাহু )

$\angle BAE = \angle CDF$ ( যেহেতু AB ।। DC এবং AF হল ছেদক )

অতএব ত্রিভুজ ABE $\cong$ ত্রিভুজ CDF

সুতরাং ত্রিভুজ ABE এর ক্ষেত্রফল = ত্রিভুজ CDF  এর ক্ষেত্রফল

এখন সমগ্র চতুর্ভুজ ABCF - ত্রিভুজ ABE = সমগ্র চতুর্ভুজ ABCF - ত্রিভুজ CDF

সামান্তরিক EBCF = সামান্তরিক ABCD

অর্থাৎ  ABCD ও EBCF সামান্তরিক দুটির ক্ষেত্রফল সমান । 

 

প্রয়োগ : ABCD ও ABEF দুটি সামান্তরিক AB রেখার বিপরীত দিকে এমন ভাবে আছে যাতে D , A ও F তিনটি বিন্দু সমরেখ না হয়। প্রমাণ করতে হবে DCEF একটি সামান্তরিক এবং ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল + ABEF সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল = DCEF সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল । 

ABCD ও ABEF দুটি সামান্তরিক AB রেখার বিপরীত দিকে এমন ভাবে আছে যাতে D , A ও F তিনটি বিন্দু সমরেখ না হয় ।

প্রমাণ করতে হবে

1. DCEF একটি সামান্তরিক
2. ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল + ABEF সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল = DCEF সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল । 

প্রমাণ : ABCD একটি সামান্তরিক ।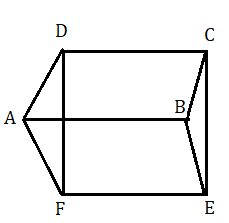 

অতএব AB ।। DC এবং AB = DC .............(i)

আবার ABEF একটি সামান্তরিক । 

অতএব AB ।। EF এবং AB = EF ............(ii)

(i) ও (ii) থেকে পাই 

DC ।। EF এবং DC = EF 

অতএব চতুর্ভুজ DCEF একটি সামান্তরিক । 

সুতরাং DF = CE .

এখন ত্রিভুজ ADF ও ত্রিভুজ BCE এর 

AD = BC ( যেহেতু ABCD সামান্তরিকের বিপরীত বাহু )

AF = BE ( যেহেতু ABEF সামান্তরিকের বিপরীত বাহু )

DF = CE 

অতএব  ত্রিভুজ ADF $\cong$ ত্রিভুজ BCE

অতএব  ত্রিভুজ ADF =  ত্রিভুজ BCE

এখন বহুভুজ DAFEC এর ক্ষেত্রফল - ত্রিভুজ ADF =  বহুভুজ DAFEC এর ক্ষেত্রফল - ত্রিভুজ BCE

DCEF সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল = বহুভুজ DAFEBC এর ক্ষেত্রফল 

বহুভুজ DAFEBC এর ক্ষেত্রফল = DCEF সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল

ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল + ABEF সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল = DCEF সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল । 

 

সামান্তরিকের ক্ষেত্রফল = ভূমি $\times$ উচ্চতা এর প্রমাণ 

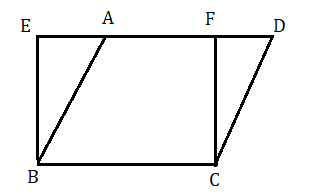মনে করি ABCD একটি সামান্তরিক 

প্রমাণ করতে হবে ABCD সামান্তরিক আকারের ক্ষেত্রফল = ভূমি $\times$ উচ্চতা

অঙ্কন : BC কে ভূমি করে BC ও AD সমান্তরাল যুগলের মধ্যে একটি আয়তক্ষেত্র BCFE অঙ্কন করা হল। যা বর্ধিত AD ও AD কে যথাক্রমে E ও F বিন্দুতে ছেদ করেছে । 

প্রমাণ : সামান্তরিক ABCD ও আয়তক্ষেত্র BCFE একই ভূমি BC এবং একই সমান্তরাল যুগল BC ও ED এর মধ্যে অবস্থিত । 

সুতরাং ABCD সামান্তরিকের ক্ষেত্রফল = BCFE আয়তক্ষেত্রের ক্ষেত্রফল 

আমরা জানি BCFE  আয়তক্ষেত্রের ক্ষেত্রফল

= দৈর্ঘ্য $\times$ প্রস্থ 

= BC $\times$ EB 

= ভূমি $\times$ উচ্চতা 

অতএব ABCD সামান্তরিকের ক্ষেত্রফল = ভূমি $\times$ উচ্চতা 

অতএব সামান্তরিকের ক্ষেত্রফল =  ভূমি $\times$ উচ্চতা 

 

একই ভূমির উপর এবং একই সমান্তরাল যুগলের মধ্যে অবস্থিত ত্রিভুজের ক্ষেত্রফল সামান্তরিকের ক্ষেত্রফলের অর্ধেক । 

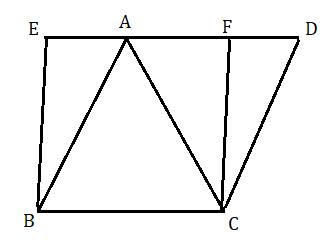মনে করি ত্রিভুজ ABC এবং সামান্তরিক EBCF একই ভূমি BC এবং একই সমান্তরাল যুগল EF ও BC এর মধ্যে অবস্থিত । 

প্রমাণ করতে হবে ত্রিভুজ ABC = $\frac{1}{2}$ সামান্তরিক EBCF 

অঙ্কন : BA এর সমান্তরাল করে CD সরলরেখা টানা হল যা বর্ধিত EF কে D বিন্দুতে ছেদ করে । 

প্রমাণ : ABCD একটি সামান্তরিক যার BC ।। AD এবং AB ।। DC ও AC হল কর্ণ। 

অতএব ত্রিভুজ ABC = $\frac{1}{2}$ সামান্তরিক ABCD 

আবার সামান্তরিক EBCF এবং সামান্তরিক ABCD একই ভূমি BC এবং একই সমান্তরাল যুগল ED ও BC এর মধ্যে অবস্থিত .

অতএব  সামান্তরিক EBCF = সামান্তরিক ABCD

অতএব ত্রিভুজ ABC = $\frac{1}{2}$ সামান্তরিক EBCF .

 

আমরা জানি ত্রিভুজের ক্ষেত্রফল = $\frac{1}{2}$ ভূমি $\times$ উচ্চতা 

আবার ত্রিভুজের ক্ষেত্রফল = $\frac{1}{2}$ সামান্তরিকের ক্ষেত্রফল 

অতএব সামান্তরিকের ক্ষেত্রফল = ভূমি $\times$ উচ্চতা 

 

ত্রিভুজের ক্ষেত্রফল = $\frac{1}{2} \times$ ভূমি $\times$ উচ্চতা প্রমাণ 

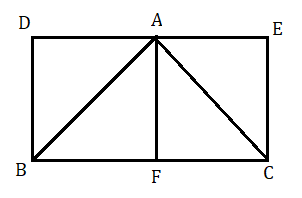মনে করি ABC একটি ত্রিভুজ যার ভূমি BC এবং $AF \bot BC$

প্রমাণ করতে হবে $\frac{1}{2} \times BC \times AF$

অঙ্কন : BC কে ভূমি করে BC এমন একটি আয়তক্ষেত্র BCED অঙ্কন করা হল যাতে , D , A ,E সমরেখ হয় । 

প্রমাণ : ত্রিভুজ ABC ও আয়তক্ষেত্র BCED একই ভূমি BC এবং একই সমান্তরাল যুগল BC ও DE এর মধ্যে অবস্থিত । 

অতএব ত্রিভুজ ABC এর ক্ষেত্রফল = $\frac{1}{2} \times$ আয়তক্ষেত্র BCED এর ক্ষেত্রফল 

= $\frac{1}{2} \times BC \times DB$

= $\frac{1}{2} \times BC \times AF$ ( যেহেতু DB = AF )

= $\frac{1}{2} \times$ ভূমি $\times$ উচ্চতা

 

প্রয়োগ : ABCD সামান্তরিকের ভিতর P যেকেনো একটি বিন্দু। প্রমাণ করতে হবে APD ত্রিভুজের ক্ষেত্রফল + BPC ত্রিভুজের ক্ষেত্রফল = $\frac{1}{2} \times$ সামান্তরিক ABCD এর ক্ষেত্রফল । 

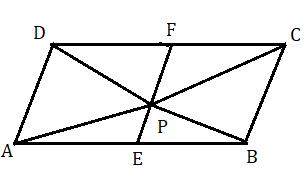ABCD সামান্তরিকের ভিতর P যেকেনো একটি বিন্দু ।

প্রমাণ করতে হবে APD ত্রিভুজের ক্ষেত্রফল + BPC ত্রিভুজের ক্ষেত্রফল = $\frac{1}{2} \times$ সামান্তরিক ABCD এর ক্ষেত্রফল । 

অঙ্কন : P বিন্দু দিয়ে AD বাহুর সমান্তরাল করে EF অঙ্কন করা হল যা AB ও DC কে  যথাক্রমে E ও F বিন্দুতে ছেদ করে । 

প্রমাণ : AEFD চতুর্ভুজের AE ।। DF ( যেহেতু AB ।। DC )

এবং AD ।। EF ( অঙ্কনানুসারে )

অতএব AEFD চতুর্ভুজটি হল একটি সামান্তরিক । 

এখন ত্রিভুজ ADP এবং সামান্তরিক AEFD একই ভূমি AD এবং একই সমান্তরাল যুগল EF ও AD এর মধ্যে অবস্থিত 

সুতরাং ত্রিভুজ ADP এর ক্ষেত্রফল = $\frac{1}{2} \times$ AEFD সামান্তরিকের ক্ষেত্রফল ...........(i)

অনুরূপভাবে প্রমাণ করা যায় ত্রিভুজ BPD ত্রিভুজের ক্ষেত্রফল = $\frac{1}{2} \times$ BCFE সামান্তরিকের ক্ষেত্রফল ...........(ii)

এখন (i) + (ii) করে পাই 

ত্রিভুজ ADP এর ক্ষেত্রফল + ত্রিভুজ BPD ত্রিভুজের ক্ষেত্রফল = $\frac{1}{2} \times$ AEFD সামান্তরিকের ক্ষেত্রফল + $\frac{1}{2} \times$ BCFE সামান্তরিকের ক্ষেত্রফল

অতএব ত্রিভুজ ADP এর ক্ষেত্রফল + ত্রিভুজ BPD ত্রিভুজের ক্ষেত্রফল = $\frac{1}{2} \times$  সামান্তরিক ABCD এর ক্ষেত্রফল । 

 

প্রয়োগ : ABC সমদ্বিবাহু ত্রিভুজের AB = AC ; BC বাহুর উপরে O যেকোনো একটি বিন্দু। O বিন্দু থেকে AB ও AC বাহুর উপরে লম্ব দূরত্ব যথাক্রমে OP এবং OQ ; B বিন্দু থেকে AC বাহুর উপরে লম্ব দূরত্ব BD ; প্রমাণ করতে হবে OP + OQ = BD .

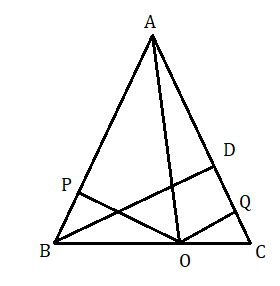ABC সমদ্বিবাহু ত্রিভুজের AB = AC ; BC বাহুর উপরে O যেকোনো একটি বিন্দু। O বিন্দু থেকে AB ও AC বাহুর উপরে লম্ব দূরত্ব যথাক্রমে OP এবং OQ ; B বিন্দু থেকে AC বাহুর উপরে লম্ব দূরত্ব BD.

প্রমাণ করতে হবে OP + OQ = BD

অঙ্কন : A , O যুক্ত করলাম । 

প্রমাণ : AOB ত্রিভুজের ক্ষেত্রফল = $\frac{1}{2} \times AB \cdot OP$..........(i)

AOC  ত্রিভুজের ক্ষেত্রফল = $\frac{1}{2} \times AC \cdot OQ$.............(ii)

(i) + (ii) করে পাই 

AOB ত্রিভুজের ক্ষেত্রফল + AOC  ত্রিভুজের ক্ষেত্রফল = $\frac{1}{2}AB \cdot OP + \frac{1}{2} \times AC \cdot OQ$

অতএব ত্রিভুজ ABC এর ক্ষেত্রফল = $\frac{1}{2}AC \cdot OP + \frac{1}{2} \times AC \cdot OQ$ ( যেহেতু AB = AC )

$\begin{array}{l}  \Rightarrow \frac{1}{2}AC \cdot BD = \frac{1}{2}AC\left( {OP + OQ} \right)\\  \Rightarrow BD = OP + OQ \end{array}$

 

প্রয়োগ: ABC সমবাহু ত্রিভুজের ভিতর O যেকোনো একটি বিন্দু। O বিন্দু থেকে BC , AC এবং AB বাহুর উপর লম্ব যথাক্রমে OP , OQ এবং OR ; প্রমাণ করতে হবে ত্রিভুজটির উচ্চতা = OP + OQ + OR .

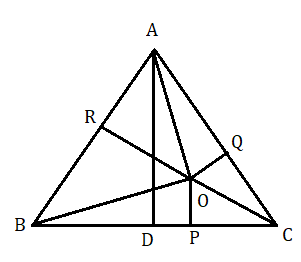ABC সমবাহু ত্রিভুজের ভিতর O যেকোনো একটি বিন্দু । O বিন্দু থেকে BC , AC এবং AB বাহুর উপর লম্ব যথাক্রমে OP , OQ এবং OR . A বিন্দু থেকে BC বাহুর উপর AD লম্ব টানা হল । সুতরাং AD হল ABC ত্রিভুজের উচ্চতা । 

আমাদের প্রমাণ করতে হবে AD = OP + OQ + OR .

অঙ্কন : O , A ; O , B এবং O , C যুক্ত করলাম । 

প্রমাণ : ত্রিভুজ ABC এর ক্ষেত্রফল = $\frac{1}{2}BC \cdot AD$

ত্রিভুজ BOC এর ক্ষেত্রফল = $\frac{1}{2}BC \cdot OP$.............(i)

ত্রিভুজ AOB এর ক্ষেত্রফল = $\frac{1}{2}AB \cdot OR$.............(ii)

ত্রিভুজ AOC এর ক্ষেত্রফল = $\frac{1}{2}AC \cdot OQ$............(iii)

এখন (i) + (ii) + (iii)

ত্রিভুজ BOC এর ক্ষেত্রফল + ত্রিভুজ AOB এর ক্ষেত্রফল + ত্রিভুজ AOC এর ক্ষেত্রফল = $\frac{1}{2}BC \cdot OP$ + $\frac{1}{2}AB \cdot OR$ + $\frac{1}{2}AC \cdot OQ$

অতএব ত্রিভুজ ABC এর ক্ষেত্রফল = $\frac{1}{2}BC \cdot OP + \frac{1}{2}BC \cdot OR + \frac{1}{2}BC \cdot OQ$

( যেহেতু ABC সমবাহু ত্রিভুজ এর AB = BC = CA )

অতএব $\frac{1}{2}BC \cdot AD$ = $\frac{1}{2}BC \cdot \left( {OP + OR + OQ} \right)$

$\begin{array}{l}  \Rightarrow AD = OP + OR + OQ\\  \Rightarrow AD = OP + OQ + OR \end{array}$

 

একই ভূমি ও একই সমান্তরাল যুগলের মধ্যে অবস্থিত ত্রিভুজের ক্ষেত্রফল সমান । 

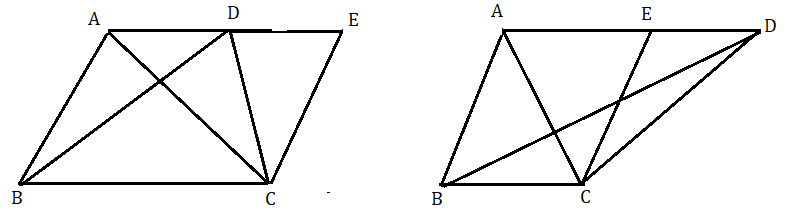
মনে করি ত্রিভুজ ABC এবং ত্রিভুজ BCD একই ভূমি BC এবং একই সমান্তরাল যুগল AD ও BC এর মধ্যে অবস্থিত । 

প্রমাণ করতে হবে ত্রিভুজ ABC এর ক্ষেত্রফল = ত্রিভুজ BCD এর ক্ষেত্রফল 

অঙ্কন : BA এর সমান্তরাল করে CE সরলরেখা টানা হল যা বর্ধিত AD কে E বিন্দুতে ছেদ করে । 

প্রমাণ : ABCE চতুর্ভুজের

AB ।। CE ( অঙ্কনানুসারে ) এবং AE ।। BC ( কল্পনানুসারে )

অতএব ABCE চতুর্ভুজটি হল সামান্তরিক । 

এখন চতুর্ভুজ ABCE ও ত্রিভুজ ABC একই ভূমি BC এবং একই সমান্তরাল যুগল AE ও BC এর মধ্যে অবস্থিত । 

অতএব ত্রিভুজ ABC = $\frac{1}{2} \times$ চতুর্ভুজ ABCE

আবার চতুর্ভুজ ABCE ও ত্রিভুজ BCD একই ভূমি BC এবং একই সমান্তরাল যুগল AE ও BC এর মধ্যে অবস্থিত । 

অতএব ত্রিভুজ BCD = $\frac{1}{2} \times$ চতুর্ভুজ ABCE

অতএব  ত্রিভুজ ABC = ত্রিভুজ BCD

 

প্রয়োগ : প্রমাণ করতে হবে যে কোনো ত্রিভুজের মধ্যমা ত্রিভুজটিকে দুটি সমান ক্ষেত্রফল বিশিষ্ট ত্রিভুজে বিভক্ত করে । 

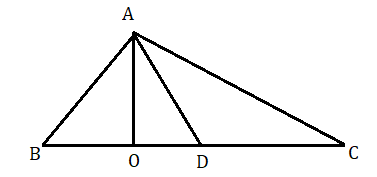মনে করি ABC একটি ত্রিভুজ এবং AD হল তার মধ্যমা অর্থাৎ BD = DC .

আমাদের প্রমাণ করতে হবে ত্রিভুজ ABD এর ক্ষেত্রফল = ত্রিভুজ ACD এর ক্ষেত্রফল । 

অঙ্কন : A থেকে BC ভূমির উপর AO লম্ব টানা হল । 

প্রমাণ : ত্রিভুজ ABD এর ক্ষেত্রফল 

= $\frac{1}{2} \times$ ভূমি $\times$ উচ্চতা 

= $\frac{1}{2}BD \cdot AO$

আবার ত্রিভুজ ACD এর ক্ষেত্রফল

= $\frac{1}{2} \times$ ভূমি $\times$ উচ্চতা 

= $\frac{1}{2}DC \cdot AO$

= $\frac{1}{2}BD \cdot AO$ ( যেহেতু BD = DC )অতএব ত্রিভুজ ABD এর ক্ষেত্রফল = ত্রিভুজ ACD এর ক্ষেত্রফল । 

 

প্রয়োগ : ABC ত্রিভুজের AD মধ্যমার উপর P যেকোনো একটি বিন্দু প্রমাণ করতে হবে যে ত্রিভুজ APB এর ক্ষেত্রফল = ত্রিভুজ APC এর ক্ষেত্রফল 

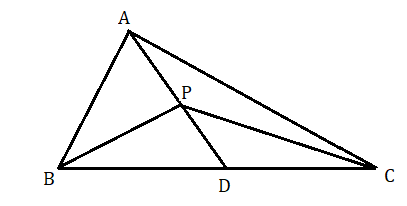ABC ত্রিভুজের AD মধ্যমার উপর P যেকোনো একটি বিন্দু । 

প্রমাণ করতে হবে যে ত্রিভুজ APB এর ক্ষেত্রফল = ত্রিভুজ APC এর ক্ষেত্রফল 

প্রমাণ : AD হল ত্রিভুজ ABC এর মধ্যমা । 

অতএব ত্রিভুজ ABD এর ক্ষেত্রফল = ত্রিভুজ ACD এর ক্ষেত্রফল......(i)

আবার ত্রিভুজ BPC ত্রিভুজের PD হল মধ্যমা 

অতএব ত্রিভুজ BPD এর ক্ষেত্রফল = ত্রিভুজ CPD এর ক্ষেত্রফল ............(ii)

এখন (i) - (ii) করে পাই 

ত্রিভুজ ABD এর ক্ষেত্রফল -  ত্রিভুজ BPD এর ক্ষেত্রফল = ত্রিভুজ ACD এর ক্ষেত্রফল - ত্রিভুজ CPD এর ক্ষেত্রফল

ত্রিভুজ ABP এর ক্ষেত্রফল = ত্রিভুজ ACP এর ক্ষেত্রফল 

 

প্রয়োগ : ABC ত্রিভুজের AB , BC ও CA বাহুগুলির মধ্যবিন্দু যথাক্রমে D , E ও F . প্রমাণ করতে হবে যে ত্রিভুজ DEF = $\frac{1}{4}$ ত্রিভুজ ABC .

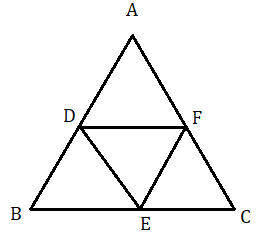ABC ত্রিভুজের AB , BC ও CA বাহুগুলির মধ্যবিন্দু যথাক্রমে D , E ও F .

প্রমাণ করতে হবে যে ত্রিভুজ DEF = $\frac{1}{4}$ ত্রিভুজ ABC .

প্রমাণ : E ও F যথাক্রমে BC ও AC এর মধ্যবিন্দু . অতএব AD ।। EF 

আবার D ও E হল যথাক্রমে AB ও BC এর মধ্যবিন্দু . অতএব DE ।। AF 

সুতরাং ADEF হল একটি সামান্তরিক এবং DF হল কর্ণ । 

অতএব ত্রিভুজ ADF = ত্রিভুজ DEF 

অনুরূপভাবে প্রমাণ করা যায় ত্রিভুজ BDE = ত্রিভুজ DEF এবং ত্রিভুজ CEF = ত্রিভুজ DEF .

সুতরাং ত্রিভুজ ABC

= ত্রিভুজ ADF + ত্রিভুজ BDE + ত্রিভুজ CEF + ত্রিভুজ DEF 

= ত্রিভুজ DEF + ত্রিভুজ DEF + ত্রিভুজ DEF + ত্রিভুজ DEF 

= 4 ত্রিভুজ DEF 

অতএব ত্রিভুজ DEF =  $\frac{1}{4}$ ত্রিভুজ ABC

*****