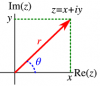
দুটি জটিল রাশির গুণফল ও ভাগফলের মডিউলাস এবং আরগুমেন্ট নির্ণয় (To find the Modulus and the Arguments of the Product and Quotient of two complex number)
মনে করি দুটি জটিল রাশি হল
[tex]\begin{array}{l}
{z_1} = {r_1}\left( {\cos {\theta _1} + i\sin {\theta _1}} \right)\\
{z_2} = {r_2}\left( {\cos {\theta _2} + i\sin {\theta _2}} \right)
\end{array}[/tex]
অতএব [tex]\left| {{z_1}} \right| = {r_1}[/tex] ও [tex]\left| {{z_2}} \right| = {r_2}[/tex]
এবং [tex]\arg {z_1} = {\theta _1}[/tex] ও [tex]\arg {z_2} = {\theta _2}[/tex]
যেখানে [tex] - \pi < {\theta _1} \le \pi [/tex] এবং [tex] - \pi < {\theta _2} \le \pi [/tex]
(1) [tex]{z_1} \cdot {z_2}[/tex] এর মডিউলাস এবং আরগুমেন্ট নির্ণয় (To find the Modulus and the Arguments of the Product of two complex number)
[tex]\begin{array}{l}
{z_1} \cdot {z_2}\\
= \left( {{r_1}\cos {\theta _1} + i{r_1}\sin {\theta _1}} \right) \cdot \left( {{r_2}\cos {\theta _2} + i{r_2}\sin {\theta _2}} \right)\\
= {r_1}{r_2}\cos {\theta _1}\cos {\theta _2} + {i^2}{r_1}{r_2}\cos {\theta _1}\sin {\theta _2} + i{r_1}{r_2}\sin {\theta _1}\cos {\theta _2} + i{r_1}{r_2}\sin {\theta _1}\sin {\theta _2}\\
= {r_1}{r_2}\left[ {\cos {\theta _1}\cos {\theta _2} - \sin {\theta _1}\sin {\theta _2} + i\left( {\sin {\theta _1}\cos {\theta _2} + \cos {\theta _1}\sin {\theta _2}} \right)} \right]\\
= {r_1}{r_2}\left[ {\cos \left( {{\theta _1} + {\theta _2}} \right) + i\sin \left( {{\theta _1} + {\theta _2}} \right)} \right]\\
= r\left( {\cos \theta + i\sin \theta } \right)
\end{array}[/tex]
যেখানে [tex]r = {r_1}{r_2}[/tex] এবং [tex]\theta = {\theta _1} + {\theta _2}[/tex]
এখন [tex]\left| {{z_1} \cdot {z_2}} \right| = r = {r_1}{r_2} = \left| {{z_1}} \right| \cdot \left| {{z_2}} \right|[/tex]
দুটি জটিল রাশির গুণফলের মডিউলাস = তাদের পৃথক পৃথক ভাবে মডিউলাস এর গুণফলের সঙ্গে সমান ।
আবার [tex] - \pi < {\theta _1} \le \pi [/tex] এবং [tex] - \pi < {\theta _2} \le \pi [/tex] অতএব [tex] - 2\pi < \theta \le 2\pi [/tex] যেখানে [tex]\theta = {\theta _1} + {\theta _2}[/tex]
[tex] - \pi < \theta + m \le \pi [/tex] যেখানে m = 0 অথবা [tex]2\pi [/tex] অথবা [tex] - 2\pi [/tex]
সুতরাং
[tex]\begin{array}{l}
\arg \left( {{z_1}{z_2}} \right)\\
= \theta + m\\
= {\theta _1} + {\theta _2} + m\\
= \arg {z_1} + \arg {z_2} + m
\end{array}[/tex]
যেখানে m = 0 অথবা [tex]2\pi [/tex] অথবা [tex] - 2\pi [/tex]
(i) যদি [tex] - \pi < \arg {z_1} + \arg {z_2} \le \pi [/tex] হয় , তবে [tex]\arg \left( {{z_1}{z_2}} \right) = \arg {z_1} + \arg {z_2}[/tex] হবে।
(ii) যদি [tex] - 2\pi < \arg {z_1} + \arg {z_2} \le - \pi [/tex] হয় , তবে [tex]\arg \left( {{z_1}{z_2}} \right) = \arg {z_1} + \arg {z_2} + 2\pi [/tex] হবে।
এবং (iii) যদি [tex]\pi < \arg {z_1} + \arg {z_2} \le 2\pi [/tex] হয় , তবে [tex]\arg \left( {{z_1}{z_2}} \right) = \arg {z_1} + \arg {z_2} - 2\pi [/tex] হবে।
(2) [tex]\frac{{{z_1}}}{{{z_2}}}[/tex] এর মডিউলাস এবং আরগুমেন্ট নির্ণয় (To find the Modulus and Argument of [tex]\frac{{{z_1}}}{{{z_2}}}[/tex] [tex]\left( {{z_2} \ne 0} \right)[/tex] )
[tex]\begin{array}{l}
\frac{{{z_1}}}{{{z_2}}}\\
= \frac{{{r_1}\left( {\cos {\theta _1} + i\sin {\theta _1}} \right)}}{{{r_2}\left( {\cos {\theta _2} + i\sin {\theta _2}} \right)}}\\
= \frac{{{r_1}\left( {\cos {\theta _1} + i\sin {\theta _1}} \right)\left( {\cos {\theta _2} - i\sin {\theta _2}} \right)}}{{{r_2}\left( {\cos {\theta _2} + i\sin {\theta _2}} \right)\left( {\cos {\theta _2} - i\sin {\theta _2}} \right)}}\\
= \frac{{{r_1}\left( {\cos {\theta _1}\cos {\theta _2} - i\sin {\theta _2}\cos {\theta _1} + i\sin {\theta _1}\cos {\theta _2} + \sin {\theta _1}\sin {\theta _2}} \right)}}{{{r_2}\left( {{{\cos }^2}{\theta _2} + {{\sin }^2}{\theta _2}} \right)}}\\
= \frac{{{r_1}}}{{{r_2}}}\left[ {\cos \left( {{\theta _1} - {\theta _2}} \right) + i\sin \left( {{\theta _1} - {\theta _2}} \right)} \right]\\
= r\left[ {\cos \theta + i\sin \theta } \right]
\end{array}[/tex]
যেখানে [tex]r = \frac{{{r_1}}}{{{r_2}}}[/tex] এবং [tex]\theta = {\theta _1} - {\theta _2}[/tex]
সুতরাং [tex]\left| {\frac{{{z_1}}}{{{z_2}}}} \right| = \sqrt {{r^2}\left( {{{\cos }^2}\theta + {{\sin }^2}\theta } \right)} = r[/tex]
অতএব [tex]\left| {\frac{{{z_1}}}{{{z_2}}}} \right| = r = \frac{{{r_1}}}{{{r_2}}} = \frac{{\left| {{z_1}} \right|}}{{\left| {{z_2}} \right|}}[/tex]
অর্থাৎ দুটি জটিল রাশির ভাগফলের মডিউলাস = জটিল রাশি দুটির মডিউলাসের ভাগফল ।
এখন [tex] - \pi < {\theta _2} \le \pi [/tex] অতএব [tex] - \pi \le - {\theta _2} < \pi [/tex] এবং [tex] - \pi < {\theta _1} \le \pi [/tex]
সুতরাং [tex] - 2\pi < {\theta _1} - {\theta _2} < 2\pi \Rightarrow - 2\pi < \theta < 2\pi [/tex]
বা , [tex] - \pi < \theta + m < \pi [/tex] যেখানে m এর মান 0 অথবা [tex]2\pi [/tex] বা -[tex]2\pi [/tex]
[tex]\begin{array}{l}
\arg \frac{{{z_1}}}{{{z_2}}}\\
= \theta + m\\
= {\theta _1} - {\theta _2} + m\\
= \arg {z_1} - \arg {z_2} + m
\end{array}[/tex]
যেখানে m এর মান 0 অথবা [tex]2\pi [/tex] বা -[tex]2\pi [/tex]