দুটি জটিল রাশির গুণফল ও ভাগফলের মডিউলাস এবং আরগুমেন্ট নির্ণয় (To find the Modulus and the Arguments of the Product and Quotient of two complex number)
মনে করি দুটি জটিল রাশি হল
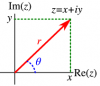
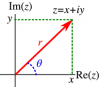
z1=r1(cosθ1+isinθ1)z2=r2(cosθ2+isinθ2)
অতএব |z1|=r1 ও |z2|=r2
এবং argz1=θ1 ও argz2=θ2
যেখানে −π<θ1≤π এবং −π<θ2≤π
(1) z1⋅z2 এর মডিউলাস এবং আরগুমেন্ট নির্ণয় (To find the Modulus and the Arguments of the Product of two complex number)
z1⋅z2=(r1cosθ1+ir1sinθ1)⋅(r2cosθ2+ir2sinθ2)=r1r2cosθ1cosθ2+i2r1r2cosθ1sinθ2+ir1r2sinθ1cosθ2+ir1r2sinθ1sinθ2=r1r2[cosθ1cosθ2−sinθ1sinθ2+i(sinθ1cosθ2+cosθ1sinθ2)]=r1r2[cos(θ1+θ2)+isin(θ1+θ2)]=r(cosθ+isinθ)
যেখানে r=r1r2 এবং θ=θ1+θ2
এখন |z1⋅z2|=r=r1r2=|z1|⋅|z2|
দুটি জটিল রাশির গুণফলের মডিউলাস = তাদের পৃথক পৃথক ভাবে মডিউলাস এর গুণফলের সঙ্গে সমান ।
আবার −π<θ1≤π এবং −π<θ2≤π অতএব −2π<θ≤2π যেখানে θ=θ1+θ2
−π<θ+m≤π যেখানে m = 0 অথবা 2π অথবা −2π
সুতরাং
arg(z1z2)=θ+m=θ1+θ2+m=argz1+argz2+m
যেখানে m = 0 অথবা 2π অথবা −2π
(i) যদি −π<argz1+argz2≤π হয় , তবে arg(z1z2)=argz1+argz2 হবে।
(ii) যদি −2π<argz1+argz2≤−π হয় , তবে arg(z1z2)=argz1+argz2+2π হবে।
এবং (iii) যদি π<argz1+argz2≤2π হয় , তবে arg(z1z2)=argz1+argz2−2π হবে।
(2) z1z2 এর মডিউলাস এবং আরগুমেন্ট নির্ণয় (To find the Modulus and Argument of z1z2 (z2≠0) )
z1z2=r1(cosθ1+isinθ1)r2(cosθ2+isinθ2)=r1(cosθ1+isinθ1)(cosθ2−isinθ2)r2(cosθ2+isinθ2)(cosθ2−isinθ2)=r1(cosθ1cosθ2−isinθ2cosθ1+isinθ1cosθ2+sinθ1sinθ2)r2(cos2θ2+sin2θ2)=r1r2[cos(θ1−θ2)+isin(θ1−θ2)]=r[cosθ+isinθ]
যেখানে r=r1r2 এবং θ=θ1−θ2
সুতরাং |z1z2|=√r2(cos2θ+sin2θ)=r
অতএব |z1z2|=r=r1r2=|z1||z2|
অর্থাৎ দুটি জটিল রাশির ভাগফলের মডিউলাস = জটিল রাশি দুটির মডিউলাসের ভাগফল ।
এখন −π<θ2≤π অতএব −π≤−θ2<π এবং −π<θ1≤π
সুতরাং −2π<θ1−θ2<2π⇒−2π<θ<2π
বা , −π<θ+m<π যেখানে m এর মান 0 অথবা 2π বা -2π
argz1z2=θ+m=θ1−θ2+m=argz1−argz2+m
যেখানে m এর মান 0 অথবা 2π বা -2π