জটিল রাশির সংক্ষিপ্তকরণ ( Complex Numbers Summary )
(1) দুটি বাস্তব রাশি x এবং y এর ক্রমযুগলকে (x , y) যদি x + iy আকারে প্রকাশ করা হয় , যেখানে [tex]i = \sqrt { - 1} [/tex] , তবে (x , y) এর ক্রমযুগলকে জটিল রাশি বলা হয়। x কে জটিল রাশির বাস্তব অংশ এবং y কে জটিল রাশির অবাস্তব অংশ বলে ।
(2) x , y বাস্তব এবং [tex]i = \sqrt { - 1} [/tex] হলে [tex]\left( {x + iy} \right)[/tex] ও [tex]\left( {x - iy} \right)[/tex] দুটি জটিল রাশিকে একে অন্যটির প্রতিযোগী বা অনুবন্দি জটিল রাশি বলা হয়। z জটিল রাশির প্রতিযোগী জটিল রাশিকে [tex]\overline z [/tex] দ্বারা প্রকাশ করা হয় ।
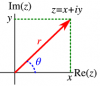
(3) [tex]z = x + iy[/tex] জটিল রাশির মডিউলাস কে ।z। দ্বারা প্রকাশ করা হয় এবং [tex]\left| z \right| = \sqrt {{x^2} + {y^2}} [/tex] . z এর অনুবন্দি জটিল রাশি [tex]\overline z [/tex] হলে [tex]\left| z \right| = \sqrt {z \cdot \overline z } [/tex] হবে ।
(4) [tex]z = x + iy[/tex] জটিল রাশির আরগুমেন্ট বা অ্যামপ্লিচিউড [tex]\theta [/tex] হলে [tex]\tan \theta = \frac{y}{x}[/tex] হবে । আরগুমেন্ট [tex]\theta [/tex] এর অসংখ্য মানের মধ্যে যে মান [tex] - \pi < \theta \le \pi [/tex] এর মধ্যে থাকবে তাকে আরগুমেন্ট এর মুখ্যমান ( Principal Value ) বলে । এই মানকে [tex]\arg z[/tex] প্রতীক দ্বারা প্রকাশ করা হয় ।
যদি [tex]z = x + iy[/tex] হয় এবং জটিল তলে
- (x , y) বিন্দু প্রথম পদে থাকে তবে , [tex]0 < \theta [/tex] এর মুখ্যমান [tex] < \frac{\pi }{2}[/tex] হবে ,
- (x , y) বিন্দু দ্বিতীয় পদে থাকে তবে , [tex]\frac{\pi }{2} < \theta [/tex] এর মুখ্যমান [tex] < \pi [/tex] হবে ,
- (x , y) বিন্দু তৃতীয় পদে থাকে তবে , [tex] - \pi < \theta [/tex] এর মুখ্যমান [tex] < - \frac{\pi }{2}[/tex] হবে ,
- (x , y) বিন্দু চতুর্থ পদে থাকে তবে , [tex] - \frac{\pi }{2} < \theta [/tex] এর মুখ্যমান < 0 হবে ।
(5) [tex]z = r\left( {\cos \theta + i\sin \theta } \right)[/tex] আকারকে z জটিল রাশির মডিউলাস - অ্যামপ্লিচিউড আকার বলা হয় । এখানে r = ।z। এবং [tex]\theta = \arg z[/tex] যেখানে [tex] - \pi < \theta \le \pi [/tex]
(6) দুটি জটিল রাশির যোগফল , বিয়োগফল , গুণফল ও ভাগফলকে X + iY আকারে প্রকাশ করা যায়। যেখানে X , Y বাস্তব ।
(7) কোনো জটিল রাশির যেকোনো অখন্ড ঘাত এবং যেকোনো মূল একটি জটিল রাশি ।
(8) x + iy = 0 হলে , x = 0 ও y = 0 হবে ।
(9) x + iy = p +iq হলে x = p ও y = q হবে ।
(10) [tex]\left| {{z_1} + {z_2}} \right| \le \left| {{z_1}} \right| + \left| {{z_2}} \right|[/tex]
(11) [tex]\left| {{z_1}{z_2}} \right| = \left| {{z_1}} \right|\left| {{z_2}} \right|[/tex]
(12) [tex]\left| {\frac{{{z_1}}}{{{z_2}}}} \right| = \frac{{\left| {{z_1}} \right|}}{{\left| {{z_2}} \right|}}[/tex]
(13) [tex]\arg \left( {{z_1}{z_2}} \right) = \arg {z_1} + \arg {z_2} + m[/tex]
এবং [tex]\arg \left( {\frac{{{z_1}}}{{{z_2}}}} \right) = \arg {z_1} - \arg {z_2} + m[/tex]
যেখানে m = 0 অথবা [tex]2\pi [/tex] অথবা [tex] - 2\pi [/tex]
(14) 1 এর ঘনমূল তিনটি হয় [tex]1,\omega ,{\omega ^2}[/tex]
যেখানে [tex]\omega = \frac{{ - 1 + i\sqrt 3 }}{2}[/tex] এবং [tex]{\omega ^2} = \frac{{ - 1 - i\sqrt 3 }}{2}[/tex] . [tex]\omega [/tex] এবং [tex]{\omega ^2}[/tex] কে 1 এর অবাস্তব ঘনমূল ।
(15) [tex]\omega [/tex] এবং [tex]{\omega ^2}[/tex] কে 1 এর অবাস্তব ঘনমূল হলে [tex]{\omega ^3} = 1[/tex] এবং [tex]1 + \omega + {\omega ^2} = 0[/tex] হবে ।