WBJEE Mathematics Question Paper 2013 (Beng)

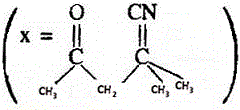
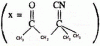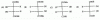1.  a এবং b প্রত্যেকটির মান 1 এবং 2 হওয়ার সম্ভাবনা সমান । ax² + bx + 1 = 0 সমীকরণের বীজদ্বয় বাস্তব হওয়ার সম্ভাবনা হল

(A) ${1 \over 2}$      (B) ${1 \over 4}$      (C) ${1 \over 8}$      (D) ${1 \over {16}}$

2.  52 টি তাসের একটি ভালোভাবে মিশ্রিত প্যাকেট থেকে একটার পর একটা তাস টানা হল না ফেরত দিয়ে (without replacement) । ছবিসহ তাস (গোলাম, রানি ও রাজা ) প্রথমবার পাওয়া যায় তৃতীয় টানে -এই ঘটনার সম্ভাবনা হল

(A) $\frac{300}{2197}$     (B) $\frac{36}{85}$      (C) $\frac{12}{85}$      (D) $\frac{4}{51}$

3.  দুটি মুদ্রা আছে যার একটি পক্ষপাতশূন্য এবং অপরটি পক্ষপাতদুষ্ট । উত্ক্ষেপণ করলে পক্ষপাতশূন্য মুদ্রাটির হেড পড়ার সম্ভাবনা ${1 \over 2}$ এবং পক্ষপাতদুষ্ট মুদ্রাটির হেড পড়ার সম্ভাবনা ${3 \over 4}$ একটি মুদ্রাকে যদৃচ্ছভাবে বেছে নিয়ে উত্ক্ষেপণ করা হল যার ফলে হেড পড়ল । এক্ষেত্রে পক্ষপাত শূন্য মুদ্রাটি নির্বাচনের সম্ভাবনা হল

(A) ${2 \over 3}$       (B) ${3 \over 5}$      (C) ${1 \over 2}$      (D) ${2 \over 5}$

4.  x + y = 1 এবং 3y = x + 3 সরলরেখাদ্বয় x² + 9y² = 9 উপবৃত্তকে P, Q এবং R বিন্দুতে ছেদ করে । PQR ত্রিভুজটির ক্ষেত্রফল হবে

(A) $\frac{36}{5}$      (B) $\frac{18}{5}$       (C) $\frac{9}{5}$      (D) $\frac{1}{5}$

5.  t একটি চলরাশি হলে 3tx - 2y + 6t = 0 এবং 3x + 2ty - 6 = 0 সরলরেখাদ্বয়ের ছেদবিন্দুর সঞ্চারপথ হবে

(A) একটি উপবৃত্ত $\frac{x^2}{4}+\frac{y^2}{9}=1$

(B) একটি উপবৃত্ত $\frac{x^2} {9}+\frac{y^2}{4}=1$

(C) একটি পরাবৃত্ত $\frac{x^2}{4}-\frac{y^2}{9}=1$

(D) একটি পরাবৃত্ত $\frac{x^2} {9}-\frac{y^2}{4}=1$

6.  x² + 4y² = 4 উপবৃত্তের উপাক্ষের ধনাত্মক প্রত্যন্ত বিন্দুগামী জ্যা সমূহের মধ্যবিন্দুর সঞ্চারপথ হবে

(A) একটি বৃত্ত যার কেন্দ্র $(\frac{1}{2},0)$ এবং ব্যাসার্ধ 1

(B) একটি অধিবৃত্ত যার নাভিবিন্দু $(\frac{1}{2},0)$ এবং নিয়ামক x = -1

(C) একটি উপবৃত্ত যার কেন্দ্র $(0,\frac{1} {2})$, পরাক্ষ 1 এবং উপাক্ষ $\frac{1}{2}$

(D) একটি পরাবৃত্ত যার কেন্দ্র $(0,\frac{1}{2})$, তির্যক অক্ষ 1 এবং অনুবন্ধী অক্ষ $\frac{1}{2}$

Ans: (No Option is correct)

7.  x² + y² = 169 বৃত্তের উপরিস্থ একটি বিন্দু P । Q = (5, 12) এবং R = (-12, 5) হলে $\angle QPR$ -এর মান হল

(A) $\frac{\pi}{6}$      (B) $\frac{\pi}{4}$       (C) $\frac{\pi}{3}$       (D) $\frac{\pi}{2}$

8.  (1, 2) এবং (-2, 1) বিন্দুদ্বয় থেকে একটি গতিশীল বিন্দুর দূরত্বের বর্গদ্বয়ের সমষ্টি সর্বদা 6 হলে উক্ত বিন্দুটির সঞ্চারপথ হবে

(A) একটি সরলরেখা $y-\frac {3}{2} = -3(x+ \frac {1}{2})$

(B) একটি বৃত্ত যার কেন্দ্র $(-\frac{1}{2}, \frac {3}{2})$ এবং ব্যাসার্ধ $\frac{1}{\sqrt2}$

(C) একটি অধিবৃত্ত যার নাভিবিন্দু (1,2) এবং নিয়ামকটি (-2, 1) বিন্দুগামী

(D) একটি উপবৃত্ত যার নাভিদ্বয় হল (1, 2) এবং (-2, 1)

9.  (0, 0), (2, 6), (6, 2) বিন্দুত্রয়গামী একটি বৃত্ত x অক্ষকে ছিন্ন করে P ≠ (0, 0) বিন্দুতে । মূলবিন্দু O হলে OP -এর দৈর্ঘ্য হবে

(A) $\frac{5}{2}$        (B) $\frac{5}{\sqrt2}$        (C) 5        (D) 10

10.  t একটি চলরাশি হলে x - 2y = t এবং $x + 2y = \frac {1} {t}$ সরলরেখাদ্বয়ের ছেদবিন্দুগুলির সঞ্চারপথ হবে

(A) একটি সরলরেখা x=y

(B) একটি বৃত্ত যার কেন্দ্র, মূলবিন্দু এবং ব্যাসার্ধ 1

(C) একটি উপবৃত্ত যার কেন্দ্র, মূলবিন্দু এবং একটি নাভি $(\frac{2}{\sqrt5},0)$

(D) একটি পরাবৃত্ত যার কেন্দ্র, মূলবিন্দু এবং একটি নাভি $(\frac{\sqrt5}{2},0)$

11.   সেট {1, 2,.....,11} থেকে {1, 2,.....,10} সেটের উপরিচিত্রণের (onto functions) সংখ্যা হল

(A) $5 \times | \underline {11}$      (B) $|\underline {10}$       (C) ${{|\underline {11}} \over 2}$      (D) $10 \times |\underline {11}$

12.  p(x) হল একটি দ্বিঘাত রাশিমালা (quadratic polynomial) যার ধ্রুবক পদ 1 । p(x) কে x - 1 এবং x + 1 দ্বারা ভাগ করলে ভাগশেষ হয় যথাক্রমে 2 এবং 4 । p(x) = 0 সমীকরণের বীজদ্বয়ের যোগফল হবে

(A) -1       (B) 1       (C) $-\frac{1}{2}$       (D) $\frac{1}{2}$

13.  $x \to 0$ হলে $[\frac {1}{x^2} + \frac {(2013)^x}{e^x-1} + \frac {1}{e^x-1}]$ রাশিমালাটির সীমামান

(A) + ∞ অভিমুখী        (B) - ∞ অভিমুখী        (C) $log_e (2013)$ -এর সমান        (D) অস্তিত্বহীন

14.  এগারোটি আপেল একটি বালিকা এবং একটি বালকের মধ্যে বন্টন করা হলে নিম্নের কোন উক্তিটি সত্য হবে ?

(A) কমপক্ষে একজন 7 টি আপেল পাবে

(B) বালিকাটি কমপক্ষে 4 টি আপেল পাবে অথবা বালকটি কমপক্ষে 9 টি আপেল পাবে

(C) বালিকাটি কমপক্ষে 5 টি আপেল পাবে অথবা বালকটি কমপক্ষে 8 টি আপেল পাবে

(D) বালিকাটি কমপক্ষে 4 টি আপেল পাবে অথবা বালকটি কমপক্ষে 8 টি আপেল পাবে

Ans: ()

15.  $z_1 = 2 + 3i$ এবং $z_2 = 3 + 4i$ হল জটিল তলের ওপর অবস্থিত দুটি বিন্দু । তাহলে যেসমস্ত জটিলরাশি $z$ এর জন্য $|z-z_1|^2+|z-z_2|^2=|z_1-z_2|^2$ সমীকরণটি সিদ্ধ হয়, জটিল তলে তাদের জ্যামিতিক রূপ হল

(A) একটি সরলরেখা         (B) একটি বিন্দু         (C) একটি বৃত্ত         (D) সরলরেখা যুগল

16.  5 টি সংখ্যার অনোন্যক সমান্তর প্রগতিতে আছে । যদি মধ্যম পদ 1 এবং দ্বিতীয় ও চতুর্থ পদের অনুপাত 2 : 1 হয়, তবে প্রথম তিনটি পদের যোগফল হবে

(A) 11/2        (B) 5        (C) 2        (C) 14/3

17.  ধরি $P=\begin{pmatrix} \cos \frac {\pi}{4} & - \sin \frac {\pi}{4} \\ \sin \frac {\pi}{4} & \cos \frac {\pi}{4} \end{pmatrix}$ এবং $X=\begin{pmatrix} \frac {1}{\sqrt2} \\ \frac{1}{\sqrt2} \end{pmatrix}$ । তাহলে $P^3X$ হবে

(A) $\begin{pmatrix} 0 \\ 1 \end{pmatrix}$       (B) $\begin{pmatrix} -\frac{1}{\sqrt2} \\ \frac{1} {\sqrt2} \end{pmatrix}$     (C) $\begin{pmatrix} -1 \\ 0 \end{pmatrix}$       (D) $\begin{pmatrix} -\frac{1} {\sqrt2} \\ - \frac{1}{\sqrt2} \end{pmatrix}$

18.  x² - x + 1 = 0 -এর বীজদ্বয় α এবং ß হলে, α²⁰¹³ + ß²⁰¹³ -এর মান হবে

(A) 2       (B) -2        (C) -1        (D) 1

19.  যদি ধনাত্মক অখন্ড সংখ্যাত্রয় x, y, z সমীকরণ x + y + z = 10 -কে সিদ্ধ করে, তবে সমীকরণটির সমাধানগুলির সংখ্যা হবে

(A) 36        (B) 55        (C) 72        (D) 45

20.  $\int_{-1}^{+1} \{\frac {x^{2013}}{e^{|x|} (x^2 + \cos x)} + \frac {1}{e^{| x|}} \}dx$ -এর মান হল

(A) 0       (B) 1 - e¹       (C) 2e¹       (D) 2(1 - e¹)

21.  $0 \le P, Q \le \frac {\pi}{2}$, -এর জন্য যদি $\sin P + \cos Q = 2$ হয়, তাহলে $\tan (\frac {P + Q}{2})$ -এর মান হল

(A) 1       (B) $\frac{1}{\sqrt2}$         (C) $\frac{1}{2}$         (D) $\frac{\sqrt3}{2}$

22.  ধরা যাক $f(x) = 2^{100}x + 1$ এবং $g(x) = 3^{100}x + 1$ । তাহলে যেসব বাস্তব সংখ্যা x -এর জন্য $f(g (x)) = x$ সমীকরণটি সিদ্ধ হয়, তাহলে সেট হল

(A) শূন্য সেট (empty)       (B) একপদী সেট (singleton)        (C) একটি সসীম সেট যার মধ্যে একাধিক পদ আছে        (D) অসীম সেট

23.  $x \to 0$ হলে $\{\frac{1}{x}\sqrt{1+x}-\sqrt{1+\frac{1}{x^2}}\}$ -এর সীমামান হল

(A) অস্তিত্বহীন         (B) 1/2        (C) 0        (D) 1

24.   cos²75° + cos²45° + cos²15° - cos²30° - cos²60° -এর মান হল

(A) 0        (B) 1        (C) 1/2         (D) 1/4

25.   $\cos^6 \theta + \sin^6 \theta$ -এর গরিষ্ঠ এবং লঘিষ্ঠ মান যথাক্রমে

(A) 1 এবং 1/4        (B) 1 এবং 0        (C) 2 এবং 0        (D) 1 এবং 1/2

26.   ধরা যাক $z = x+iy$ যেখানে x ও y বাস্তব সংখ্যা এবং $i = \sqrt {-1}$ । (x, y) বিন্দুগুলি যার জন্য $\frac {z-1}{z-i}$ বাস্তব , অবস্থান করে

(A) একটি উপবৃত্তের ওপর        (B) একটি বৃত্তের ওপর       (C) একটি অধিবৃত্তের ওপর       (D) একটি সরলরেখার ওপর

27.   যদি a, b, c সংখ্যাগুলি A.P. -তে থাকে তাহলে ax + 2by + c = 0 সরলরেখাটি সর্বদা একটি নির্দিষ্ট বিন্দু দিয়ে যায়— যার স্থানাঙ্ক হল

(A) (1, -1)        (B) (-1, 1)       (C) (1, -2)        (D) (-2, 1)

28.  2x² + 5xy - 12y² = 0 সমীকরণটি নির্দেশ করে

(A) বৃত্তকে

(B) সরলরেখাযুগলকে যে রেখা দুটি একে অপরকে ছেদ করে, কিন্তু লম্বভাবে নয়

(C) লম্বভাবে ছেদ করে এমন সরলরেখাযুগলকে

(D) পরাবৃত্তকে

29.  3x² + 3y² - 9x + 6y + 5 = 0 বৃত্তটির একটি ব্যাসের এক প্রান্তের স্থানাঙ্ক (1, 2) হলে, অপর প্রান্তের স্থানাঙ্ক হল

(A) (2, 1)        (B) (2, 4)        (C) (2, -4)       (D) (-4, 2)

30.  y = x রেখাটি $\frac {x^2}{9} - \frac {y^2}{25} = 1$ পরাবৃত্তটিকে P ও Q বিন্দুতে ছেদ করে । একটি উপবৃত্তের পরাক্ষ PQ এবং উপাক্ষের দৈর্ঘ্য $\frac {5}{ \sqrt 2}$ । উপবৃত্তটির উৎকেন্দ্রতা হল

(A) $\frac {\sqrt 5}{3}$        (B) $\frac {5}{\sqrt 3}$         (C) $\frac {5}{9}$        (D)$\frac {25}{9}$

Ans: ()

31.  x → 0 হলে x sin (e^1/x) -এর সীমামান

(A) 0        (B) 1       (C) e/2      (D) থাকে না

32.  $1000[\frac {1}{1 \times 2} + \frac {1}{2 \times 3} + \frac {1}{3 \times 4} + ... + \frac {1}{999 \times1000}]$ -এর মান হল

(A) 1000       (B) 999        (C) 1001        (D) 1/999

33.   ধরা যাক $I = \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix}$ এবং $P = \begin{pmatrix} 1 & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & -2 \end{pmatrix}$ ।  তবে $P^3 + 2P^2$ ম্যাট্রিক্সটি

(A) P -এর সমান        (B) I - P -এর সমান        (C) 2I + P -এর সমান        (D) 2I - P -এর সমান

34.  $\begin{vmatrix} 1+a^2-b^2 & 2ab & -2b\\ 2ab & 1- a^2+b^2 & 2a \\ 2b & -2a & 1-a^2-b^2 \end{vmatrix}$ নির্ণায়কটির মান হল

(A) 0       (B) (1 + a² + b² )        (C) (1 + a² + b² )²        (D) (1 + a² + b²)³

35.  x² + ax + b = 0, (b ≠ 0) দ্বিঘাত সমীকরণটির বীজদ্বয় α এবং ß হলে $\alpha - \frac {1}{\beta}$ ও $\beta - \frac {1}{\alpha}$ যে দ্বিঘাত সমীকরণের বীজ, তা হল

(A) $ax^2+a(b-1)x+(a-1)^2=0$

(B) $bx^2+a(b-1)x+(b-1)^2=0$

(C) $x^2+ax+b=0$

(D) $abx^2+bx +a=0$

36.  একটি উপবৃত্তের নাভিদ্বয়ের মধ্যেকার দূরত্ব যদি তার নাভিলম্বের সাথে সমান হয়, তাহলে উপবৃত্তটির উৎকেন্দ্রতা হল

(A) $\frac{1}{4}(\sqrt5-1)$       (B) $\frac{1}{2}(\sqrt5+1)$       (C) $\frac{1}{2} (\sqrt5-1)$      (D) $\frac{1}{4}(\sqrt5+1)$

37.  (1, 1) বিন্দুগামী এবং x² + y² - 6x - 8 = 0 ও x² + y² - 6 = 0 -এর ছেদ বিন্দুগামী বৃত্তের সমীকরণ হল

(A) x² + y² + 3x - 5 = 0

(B) x² + y² - 4x + 2 = 0

(C) x² + y² + 6x - 4 = 0

(D) x² + y² - 4y -2 = 0

38.  (2, -3) বিন্দুগামী এবং (-1, 2) বিন্দু থেকে 8 একক দূরত্বে থাকা সরলরেখার সংখ্যা

(A) অসীম         (B) 4       (C) 2       (D) 0

39.  ছটি সংখ্যা G.P. -তে আছে । এদের গুণফল 1000 এবং চতুর্থ পদ হল 1 ।  তবে শেষ পদ হবে

(A) 1000         (B) 100         (C) 1/100         (D) 1/1000

40.  যদি ax² + bx + c = 0 দ্বিঘাত সমীকরণটির বীজদ্বয় α, β হয় এবং 3b² = 16ac হয়, তাহলে

(A) α = 4β অথবা ß = 4α      (B) α = -4β অথবা β = -4α      (C) α = 3β অথবা β = 3α     (D) α = -3β অথবা β = -3α

41.  3 x 3 ম্যাট্রিক্সদের সেট, যে ম্যাট্রিক্সগুলোর সমস্ত পদ বাস্তব সংখ্যা, সেই সেটের মধ্যে একটি সম্পর্ক (relation) সংজ্ঞাত হল এভাবে ; ম্যাট্রিক্স A ম্যাট্রিক্স B এর সঙ্গে সম্পর্কিত হবে যদি এবং কেবলমাত্র যদি কোনো একটি 3 x 3 নন-সিঙ্গুলার ম্যাট্রিক্স P পাওয়া যায় যাতে B = P^-1AP হয় । তাহলে সম্পর্কটি

(A) স্বসম (Reflexive) ও প্রতিসম (Symmetric) কিন্তু সংক্রমণ (Transitive) নয়

(B) স্বসম ও সংক্রমণ কিন্তু প্রতিসম নয়

(C) প্রতিসম ও সংক্রমণ কিন্তু স্বসম নয়

(D) একটি সমতুল্যতা (Equivalence) সম্পর্ক

42.  যে কোনো দুটি বাস্তব সংখ্যা a ও b -এর জন্য আমরা ধরি a R b যদি এবং কেবলমাত্র যদি sin² a + cos² b = 1 হয় । R সম্পর্কটি হল

(A) স্বসম কিন্তু প্রতিসম নয়      (B) প্রতিসম কিন্তু সংক্রমণ নয়      (C) সংক্রমণ কিন্তু স্বসম নয়     (D) একটি সমতুল্যতা সম্পর্ক

43.  x² + 4xy + 8y² = 64 বক্ররেখাটির স্পর্শকগুলো x অক্ষের সমান্তরাল হবে কেবলমাত্র

(A) (0, 2√2) এবং (0, -2√2) বিন্দুতে

(B) (8, -4) এবং (-8, 4) বিন্দুতে

(C) (8√2, -2√2) এবং (-8√2, 2√2) বিন্দুতে

(D) (8,0) এবং (-8,0) বিন্দুতে

44.  ধরা যাক $f(x) = \left\{ {\matrix{ {{x^3} - 3x + 2} & {x < 2} \cr {{x^3} - 6{x^2} + 9x + 2} & {x \ge 2} \cr } } \right.$ তবে

(A) $\lim \limits_{x \to 2} f(x)$ -এর অস্তিত্ব নেই

(B) x = 2 বিন্দুতে ƒ সন্তত (continuous) নয়

(C) x = 2 বিন্দুতে ƒ সন্তত (continuous) কিন্তু অবকলনযোগ্য নয়

(D) x = 2 বিন্দুতে ƒ সন্তত (continuous) কিন্তু অবকলন যোগ্য

45.  $I = \int_0^{\pi \over 4}( \tan^{n+1}x)dx + \frac {1}{2} \int_0^{\pi \over 2} \tan^{n-1} (x/2)dx$ -এর মান

(A) $\frac {1}{n}$       (B) $\frac {n+2}{2n+1}$       (C) $\frac {2n-1}{n}$       (D) $\frac {2n-3}{3n-2}$

46.  $x \to \infty$ হলে $\sum \limits_{n=1}^{1000}(-1)^nx^n$ -এর সীমা মান

(A) থাকে না       (B) আছে এবং তা হল 0       (C) আছে এবং + ∞ অভিমুখী        (D) আছে এবং - ∞ অভিমুখী

47.  ধরা যাক ƒ(θ) = (1 + sin²θ)(2 - sin²θ) । তবে θ -র সমস্ত মানের জন্য

(A) ƒ(θ) > ${9 \over 4}$       (B) ƒ(θ) < 2      (C) ƒ(θ) > ${11 \over 4}$      (D) 2 ≤ ƒ(θ) ≤ ${9 \over 4}$

48.  যদি ƒ(x) = e^x(x - 2)² হয়, তাহলে

(A) (- ∞ ,0) ও (2, ∞) -তে ƒ ক্রমবর্ধমান ও (0, 2) -তে ক্রমহ্রাসমান

(B) (- ∞ ,0) -তে ƒ ক্রমবর্ধমান ও (0, ∞) -তে ক্রমহ্রাসমান

(C) (2, ∞) -তে ƒ ক্রমবর্ধমান ও (- ∞, 0) -তে ক্রমহ্রাসমান

(D) (0, 2) -তে ƒ ক্রমবর্ধমান এবং (- ∞ ,0) ও (2, ∞) -তে ক্রমহ্রাসমান

49.  ধরা যাক n একটি ধনাত্মক যুগ্ম অখন্ড সংখ্যা ।  (1 + x)ⁿ -এর বিস্তারে সর্বাধিক সহগ ও দ্বিতীয় সর্বাধিক সহগের অনুপাত হল 11 : 10  ।  তবে (1 + x)ⁿ -এর বিস্তারের পদসংখ্যা হল

(A) 20        (B) 21       (C) 10        (D) 11

50.  পাঁচটি সংখ্যা A.P. -তে আছে, যেখানে সাধারণ অন্তর ≠ 0  ।  যদি প্রথম, তৃতীয় ও চতুর্থ পদ G.P. -তে থাকে, তাহলে

(A) পঞ্চম পদ সর্বদা 0 হবে        (B) প্রথম পদ সর্বদা 0 হবে       (C) মধ্য পদ সর্বদা 0 হবে       (D) মধ্য পদ সর্বদা -2 হবে

51.  ধরা যাক, $f(x) = \exp (x^{\frac {1}{x}}), x>0$ যেখানে exp(x) = e^x । [2, 5] অন্তরালে ƒ -এর অবম মান হবে

(A) $\exp (e^{\frac{1}{e}})$       (B) $\exp (2^{\frac {1}{2}})$       (C) $\exp (5^{\frac{1}{5}})$      (D) $\exp (3^{\frac{1}{3}})$

52.  $f(x)=2|x-1|+|x-2|$ -এর অবম মান হবে

(A) 0        (B) 1        (C) 2        (D) 3

53.  $\frac {1}{1 \times 2}{^{25}}C_0 + \frac {1}{2 \times 3}{^{25}}C_1 + \frac {1}{3 \times 4}{^{25}}C_2 +...+ \frac {1}{26 \times 27}{^{25}}C_{25}$ শ্রেণীটির যোগফল হল

(A) $\frac {2^{27} - 1}{26 \times 27}$      (B) $\frac {2^{27}-28}{26 \times 27}$      (C) $\frac {1}{2}(\frac {2^{26}+1}{26 \times 27})$     (D) $\frac {2^{26} -1}{52}$

54.  যদি P, Q, R একটি সমদ্বিবাহু ত্রিভুজের তিনটি কোণ হয় যেখানে $\angle P = {\pi \over 2}$ তবে $(\cos \frac {P}{3} - i \sin {P \over 3})^3 + ( \cos Q + i \sin Q)( \cos R -i \sin R ) + ( \cos P -i \sin P )( \cos Q -i \sin Q)( \cos R -i \sin R)$ -এর মান

(A) i       (B) -i        (C) 1        (D) -1

55.  ধরা যাক $f:\mathbb{R}\to\mathbb{R}$ যেখানে ƒ হল ইনজেকটিভ এবং $f(x)f(y)=f(x+y)$ সকল বাস্তব $x,y \in \mathbb{R}$ -এর জন্য । যদি $f(x), f(y), f(z)$ G.P. -তে থাকে তবে, x, y, z

(A) সর্বদা A.P. -তে থাকবে

(B) সর্বদা G.P. -তে থাকবে

(C) x, y, z -এর মানের ওপর নির্ভরশীল হয়ে A.P. -তে থাকবে

(D) x, y, z -এর মানের ওপর নির্ভরশীল হয়ে G.P. -তে থাকবে

56.  $\int_1^2e^x(log_ex+\frac{x+1}{x})dx$ সমাকলটির মান হল

(A) $e^2(1+log_e2)$       (B) $e^2-e$       (C) $e^2(1+log_e2)-e$        (D) $e^2-e(1+log_e2)$

57.  $\frac{1}{2}log_{\sqrt3}(\frac{x+1}{x+5})+log_9(x+5) ^2=1$ সমীকরণটির সমাধানের সংখ্যা হল

(A) 0       (B) 1       (C) 2        (D) অসীম

58.  ধরা যাক $P=1+\frac {1}{2 \times 2} + \frac {1}{3 \times 2^2}+......$ এবং $Q=\frac {1}{1 \times 2}+ \frac {1}{3 \times 4}+ \frac {1}{5 \times 6}+......$ তবে

(A) P = Q       (B) 2P = Q       (C) P = 2Q       (D) P = 4Q

59.  অধিবৃত্ত y = x² - 4x + 5 এবং সরলরেখা y = x + 1 দ্বারা সীমাবদ্ধ ক্ষেত্র হল

(A) 1/2        (B) 2        (C) 3        (D) 9/2

60.  যদি $f(x)= \sin x+2 \cos^2 x$, $\frac {\pi}{4} \le x \le \frac {3 \pi}{4}$ হয়, তবে

(A) $x=\frac {\pi}{4}$ -য়ে ƒ -এর অবম মান থাকবে

(B) $x=\frac {\pi}{2}$ -য়ে ƒ -এর চরম মান থাকবে

(C) $x=\frac {\pi}{2}$ -য়ে ƒ -এর অবম মান থাকবে

(D) $x= \sin^{-1}(\frac {1}{4})$ -য়ে ƒ -এর চরম মান থাকবে

61.  একটি নৈবক্তিক (objective) প্রশ্নপত্রে পাঁচটি প্রশ্ন আছে  ।  এর মধ্যে তিনটি প্রশ্নের প্রত্যেকটির চারটি করে বিকল্প (A, B, C, D) আছে এবং একটি বিকল্প সঠিক । অন্য দুটি প্রশ্নে দুটি করে বিকল্প আছে । ঠিক ও ভুল । একজন পরীক্ষার্থী ইচ্ছেমতো বিকল্পগুলো টিক (tick) মারল । অন্তত চারটি প্রশ্নের সঠিক বিকল্পে টিক মারার সম্ভাবনা হল

(A) $\frac {5}{32}$       (B) $\frac {3}{128}$       (C) $\frac {3}{256}$       (D) $\frac {3}{64}$

62.  যদি x = 1, y = 1 অবকল সমীকরণ $(y^2 + 2x)\frac {dy}{dx} = y$ -এর সমাধানকে সিদ্ধ করে তাহলে সমাধানটি হল

(A) $x=y^2(1+log_ey)$

(B) $y=x^2(1+log_ex)$

(C) $x=y^2(1-log_ey)$

(D) $y=x^2(1- log_ex)$

63.  বক্ররেখা গুচ্ছের মুলবিন্দু এবং একটি বিন্দুতে অঙ্কিত স্পর্শকের ভিতরে y অক্ষ দ্বারা ছেদিতাংশের দৈর্ঘ্য স্পর্শবিন্দুর কোটির (ordinate) তিনগুন, তাহলে বক্ররেখা গুচ্ছের সমীকরণ হল

(A) xy = c, c একটি ধ্রুবক       (B) xy² = c, c একটি ধ্রুবক       (C) x²y = c, c একটি ধ্রুবক       (D) x²y² = c, c একটি ধ্রুবক

64.  অবকল সমীকরণ $y \sin (x/y)dx = (x \sin (x/y) - y) dy$ satisfying $y(\pi /4) = 1$ -এর সমাধান হল

(A) $\cos \frac {x}{y} =-log_ey + \frac {1}{\sqrt2}$

(B) $\sin \frac {x}{y} = log_ey + \frac {1} {\sqrt2}$

(C) $\sin \frac {x}{y} = log_ex- \frac {1}{\sqrt 2}$

(D) $\cos \frac {x}{y} =-log_ex - \frac {1} {\sqrt 2}$

Ans: ()

65.   x + y = 4 এবং x - y = 2 সরলরেখাদ্বয়ের ছেদবিন্দুগামী একটি সরলরেখা x অক্ষের সঙ্গে $tan^ {-1}(3/4)$ কোণে নত । সরলরেখাটির অধিবৃত্ত y² = 4(x - 3) কে (x₁, y₁) এবং (x₂, y₂) বিন্দুতে ছেদ করে, তাহলে |x₁ - x₂| =

(A) ${16 \over 9}$        (B) ${32 \over 9}$       (C) ${40 \over 9}$       (D) ${80 \over 9}$

66.  যদি $\sin^2 \theta + 3 \cos \theta = 2$, তবে $\cos^3 \theta + \sec^3 \theta$ =

(A) 1       (B) 4       (C) 9      (D) 18

67.  যে কোনো বাস্তব সংখ্যা a -এর জন্য [a] -এর থেকে অর্থ হল সর্বোচ্চ পূর্ণ সংখ্যা যা a থেকে ছোটো অথবা সমান । তা হলে $\int_{-{\pi \over 2}}^{\pi \over 2}[ \sin x \cos x]dx$ হবে

(A) ${\pi \over 2}$       (B) $\pi$       (C) $- \pi$      (D) $-{\pi \over 2}$

68.  যদি $x = 1 + \frac {1}{2 \times |\underline 1} + \frac {1}{4 \times |\underline2} + \frac {1}{8 \times | \underline3} +......$ এবং $y = 1 + \frac {x^2}{|\underline1} + \frac {x^4}{|\underline 2} + \frac {x^6}{ | \underline 3} +......$ হয়, তবে $log_ey$ এর মান হবে

(A) e       (B) e²        (C) 1       (D) 1/e

69.  যদি $P=\begin{pmatrix} 2 & -2 & -4\\ -1 & 3 & 4\\ 1 & -2 & -3 \end{pmatrix}$ হয়, তবে $P^5$ =

(A) P       (B) 2P       (C) -P        (D) -2P

70.  $\frac {1^2 + 2^2}{|\underline 3} + \frac {1^2 + 2^2 + 3^2}{| \underline 4} + \frac {1^2 + 2^2 + 3^2 + 4^2} {|\underline 5}+.......$ এই অসীম শ্রেণীটির মান হল

(A) e        (B) 5e        (C) $\frac {5e}{6} - \frac {1}{2}$       (D) $\frac{5e}{6}$

71.  $\int_{\pi \over 6}^{\pi \over 3} \frac {(\sin x - x \cos x)}{x(x + \sin x)}dx$ সমাকলটির মান হল

(A) $log_e(\frac{2(\pi+3)}{2\pi+3\sqrt3})$       (B) $log_e(\frac{\pi+3}{2(2\pi +3\sqrt3)})$       (C) $log_e(\frac{2\pi+3\sqrt3}{2(\pi+3)})$      (D) $log_e(\frac{2(2\pi+3\sqrt3)}{\pi +3})$

72.  যদি ƒ(x) = x^2/3, x ≥ 0 হয়, তবে বক্ররেখা y = ƒ(x) এবং সরলরেখা y = x, x = 1 এবং x = 8 দ্বারা সীমাবদ্ধ অংশের ক্ষেত্রফল হবে

(A) $\frac{63}{2}$       (B) $\frac{93}{5}$       (C) $\frac{105}{7}$      (D) $\frac{129}{10}$

73.  ধরা যাক $f(x) = x( \frac {1}{x-1} + \frac {1}{x} + \frac {1}{x+1})$ , x > 1, তাহলে

(A) $f(x) \le 1$       (B) $1 < f(x) \le 2$       (C) $2 < f(x) \le 3$      (D) $f(x) > 3$

74.  F নাভিবিশিষ্ট অধিবৃত্ত y² = 4ax -এর ওপর P একটি বিন্দু । যদি P থেকে নিয়ামকের ওপর লম্বের পাদবিন্দু Q হয়, তবে $\frac {\tan \angle {PQF}}{\tan \angle {PFQ}}$ হবে

(A) 1        (B) 1/2         (C) 2        (D) 1/4

75.  ধরা যাক, $F(x) = \int_0^x \frac {\cos t}{(1 + t^2)}dt$, $0 \le x \le 2 \pi$ । তবে

(A) $(\frac {\pi}{2},\frac {3\pi}{2})$ -তে F ক্রমবর্ধমান এবং $(0,\frac{\pi}{2})$ ও $(\frac{3\pi}{2},2\pi)$ -তে F ক্রমহ্রাসমান

(B) $(0,\pi)$ -তে F ক্রমবর্ধমান এবং $(\pi,2 \pi)$ -তে F ক্রমহ্রাসমান

(C) $(\pi, 2 \pi)$ -তে F ক্রমবর্ধমান এবং $(0,\pi)$ -তে F ক্রমহ্রাসমান

(D) $(0,\frac {\pi}{2})$ ও $(\frac {3 \pi}{2}, 2\pi)$ -তে F ক্রমবর্ধমান এবং $(\frac {\pi}{2},\frac {3 \pi} {2})$ -তে F ক্রমহ্রাসমান

76.  যে সব বৃত্ত উভয় অক্ষকে এবং 4x + 3y = 12 সরলরেখাকে স্পর্শ করে এবং যাদের কেন্দ্র প্রথম পাদে থাকে তাদের সমীকরণ হল

(A) x² + y² - x - y + 1 = 0

(B) x² + y² - 2x - 2y + 1 = 0

(C) x² + y² - 12x - 12y + 36 = 0

(D) x² + y² - 6x - 6y + 36 = 0

77.  y² = x অধিবৃত্ত ও y = mx রেখার দ্বারা বেষ্টিত ক্ষেত্রের ক্ষেত্রফল ${1 \over 48}$ হলে m -এর মান হল

(A) -2        (B) -1       (C) 1        (D) 2

78.  ধরা যাক x² - bx + c = 0 সমীকরণের বীজদ্বয় sin α, cos α । নীচের কোন বিবৃতিগুলো সঠিক ?

(A) $c \le \frac {1}{2}$         (B) $b \le \sqrt {2}$         (C) $c > \frac{1}{2}$         (D) $b > \sqrt{2}$

79.  $x + y + z = 0$ $\alpha x + \beta y + \gamma z = 0$ $\alpha^2 x + \beta^2 y + \gamma^2 z = 0$ এই সমীকরণ সমূহের

(A) অদ্বিতীয় সমাধান আছে, সমস্ত $\alpha ,\beta ,\gamma$ জন্য

(B) অসীম সংখ্যক সমাধান আছে, যদি $\alpha ,\beta , \gamma$ -র মধ্যে যে-কোনো দুটির মান সমান হয়

(C) অদ্বিতীয় সমাধান আছে, যদি $\alpha ,\beta , \gamma$ সব পৃথক হয়

(D) একাধিক কিন্তু সসীম সংখ্যক সমাধান আছে যা $\alpha ,\beta ,\gamma$ -র মানের ওপর নির্ভরশীল

80.  নীচের কোনো কোনো বাস্তব অপেক্ষক (real valued function) যুগ্ম অপেক্ষক (even function) হবে না ?

(A) ƒ(x) = x³ sin x

(B) ƒ(x) = x² cos x

(C) ƒ(x) = exx³ sin x

(D) ƒ(x) = x-[x], যেখানে [x] নির্দেশ করে x বা তার চেয়ে ছোটো সর্বোচ্চ অখন্ড সংখ্যাকে

***