সমবিন্দু সংক্রান্ত উপপাদ্য

সমবিন্দু সংক্রান্ত উপপাদ্য (Theorems on Concurrence)

কয়েকটি সংজ্ঞা 

সমবিন্দু সরলরেখা ( Concurrent lines ) : দুটির বেশি ভিন্ন সরলরেখার একটি সাধারণ বিন্দু থাকলে সরলরেখাগুলিকে সমবিন্দু সরলরেখা ( Concurrent lines ) বলা হয় । 

পরিবৃত্ত : কোনো ত্রিভুজের শীর্ষবিন্দুগামী বৃত্তকে বৃত্ত কে ওই ত্রিভুজের পরিবৃত্ত বলা হয় । 

পরিকেন্দ্র : পরিবৃত্তের কেন্দ্রকে পরিকেন্দ্র বলা হয়।  ত্রিভুজের শীর্ষবিন্দুগুলি পরিকেন্দ্র থেকে সমান দূরত্বে থাকে । 

পরিব্যাসার্ধ : পরিবৃত্তের ব্যাসার্ধকে পরিব্যাসার্ধ বলা হয়। পরিকেন্দ্র থেকে ত্রিভুজের শীর্ষবিন্দু গুলির দূরত্ব পরিব্যসার্ধের সাথে সমান । 

 

ত্রিভুজের বাহুগুলির লম্বসমদ্বিখণ্ডকদ্বয় সমবিন্দু

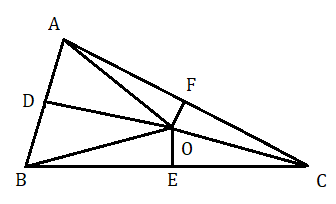মনে করি ABC একটি ত্রিভুজ D , E ও F যথাক্রমে AD , BC ও CA বাহুর মধ্যবিন্দু। D ও E বিন্দুতে যথাক্রমে AD ও BC বাহুর উপর লম্ব O বিন্দুতে মিলিত হয়েছে। O , F যুক্ত করলাম। 

প্রমাণ করতে হবে যে OF $\bot$ AC .

অঙ্কন : A , O ; B , O ও C , O যুক্ত করলাম । 

প্রমাণ : এখন ত্রিভুজ AOD ও ত্রিভুজ BOD এর মধ্যে 

AD = BD ( D , AB এর মধ্যবিন্দু )

OD সাধারণ বাহু 

এবং $\angle ADO = \angle BDO = {90^ \circ }$

সুতরাং ত্রিভুজ AOD $\cong$ ত্রিভুজ BOD

অতএব OA = OB ( সর্বসম ত্রিভুজের অনুরূপ বাহু )

অনুরূপভাবে প্রমাণ করা যায় ত্রিভুজ BOE $\cong$ ত্রিভুজ COE 

অতএব OB = OC ( সর্বসম ত্রিভুজের অনুরূপ বাহু )

সুতরাং OA = OC 

এখন ত্রিভুজ AOF ও ত্রিভুজ COF এর 

AF = CF ( F হল AC এর মধ্যবিন্দু )

OA = OC 

এবং OF হল সাধারণ বাহু 

অতএব ত্রিভুজ AOF $\cong$  ত্রিভুজ COF

অতএব $\angle AFO = \angle CFO$ ( সর্বসম ত্রিভুজের অনুরূপ কোণ )

যেহেতু AC সরলরেখার উপর OF দণ্ডায়মান হওয়ার ফলে উৎপন্ন দুটি কোণ সমান , তাই OF , AC এর উপর লম্ব হবে । 

ত্রিভুজ ABC এর বাহুগুলির লম্বসমদ্বিখণ্ডক তিনটি সমবিন্দু । 

 

প্রয়োগ : ABC ত্রিভুজের পরিকেন্দ্র O হলে , $\angle BOC$ এবং $\angle BAC$ এর সম্পর্ক নির্ণয় করতে হবে । 

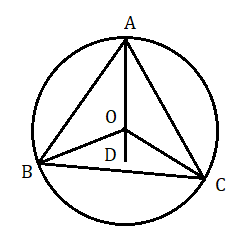ABC ত্রিভুজের পরিকেন্দ্র হল O .

প্রমাণ করতে হবে  $\angle BOC$ এবং $\angle BAC$ এর মধ্যে সম্পর্ক আছে । 

অঙ্কন : A , O যুক্ত করে D বিন্দু পর্যন্ত বর্ধিত করলাম । 

প্রমাণ : ত্রিভুজ AOB ত্রিভুজের OA = OB ( একই বৃত্তের ব্যাসার্ধ )

অতএব $\angle OAB = \angle OBA$

এখন 

$\begin{array}{l} \angle OAB + \angle OBA = \angle BOD\\  \Rightarrow \angle OAB + \angle OAB = \angle BOD\\  \Rightarrow 2\angle OAB = \angle BOD......(i) \end{array}$

অনুরূপে পাই $2\angle OAC = \angle COD$.............(ii)

এখন (i) + (ii) করে পাই 

$\begin{array}{l} 2\angle OAB + 2\angle OAC = \angle BOD + \angle COD\\  \Rightarrow 2\angle BAC = \angle BOC \end{array}$

 

ত্রিভুজের শীর্ষবিন্দু থেকে বিপরীত বাহুগুলির উপর অঙ্কিত লম্ব তিনটি সমবিন্দু 

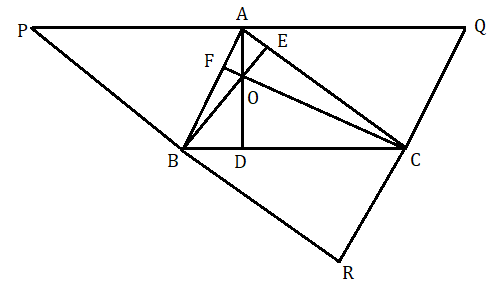মনে করি ABC ত্রিভুজের শীর্ষবিন্দু A , B ও C থেকে BC , CA ও AB বাহুর উপর যথাক্রমে AD , BE ও CF লম্ব টানা হল । 

প্রমাণ করতে হবে AD , BE ও CF হল সমবিন্দু । 

অঙ্কন : A , B ও C বিন্দু দিয়ে যথাক্রমে BC , CA ও AB বাহুর সমান্তরাল করে সরলরেখা অঙ্কন করা হল যারা পরস্পরকে যথাক্রমে P , Q ও R বিন্দুতে ছেদ করেছে । 

প্রমাণ : অঙ্কনানুসারে APBC , ABCQ ও ABRC এরা প্রত্যেকেই সামান্তরিক । 

সামান্তরিক APBC ও সামান্তরিক ABCQ থেকে পাই 

PA = BC এবং AQ = BC 

সুতরাং A হল PQ এর মধ্যবিন্দু 

অনুরূপভাবে B এবং C হল যথাক্রমে PR ও QR এর মধ্যবিন্দু । 

আবার PQ ।। BC এবং AD $\bot$ BC , সুতরাং AD $\bot$ PQ .

অনুরূপে দেখানো যায় BE $\bot$ PR এবং CF $\bot$ QR .

সুতরাং দেখা যাচ্ছে AD , BE এবং CF যথাক্রমে PQ , PR এবং QR এর লম্বসমদ্বিখণ্ডক । 

সুতরাং AD , BE এবং CF হল সমবিন্দু । 

অতএব  ABC ত্রিভুজের শীর্ষবিন্দু A , B ও C থেকে BC , CA ও AB বাহুর উপর যথাক্রমে AD , BE ও CF অঙ্কিত লম্ব গুলি সমবিন্দু । 

 

ত্রিভুজের শীর্ষবিন্দু গুলি থেকে বিপরীত বাহুর উপর অঙ্কিত লম্ব গুলি সমবিন্দু অর্থাৎ তারা একটি বিন্দুতে পরস্পরকে ছেদ করেছে এই সাধারণ বিন্দুটিকে বলা হয় লম্ববিন্দু। উপরের চিত্রে O হল ত্রিভুজ ABC এর লম্ববিন্দু । ABC ত্রিভুজের D , E ও F বিন্দুগুলি পরপর যুক্ত করে যে ত্রিভুজ পাওয়া যায় সেই ত্রিভুজটিকে পদ ত্রিভুজ ( Pedal Triangle ) বলে । 

 

ত্রিভুজের কোণগুলির অন্তর্সমদ্বিখণ্ডক তিনটি সমবিন্দু । 

মনে করি ABC ত্রিভুজের $\angle B$ ও $\angle C$ এর অন্তর্সমদ্বিখণ্ডক O বিন্দুতে পরস্পরকে ছেদ করেছে । A , O যুক্ত করা হল । 

প্রমাণ করতে হবে AO হল $\angle A$ এর অন্তর্সমদ্বিখণ্ডক ।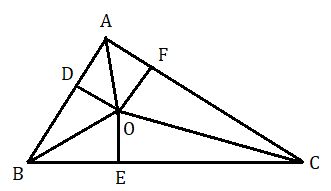 

অঙ্কন : O বিন্দু থেকে AB , BC এবং CA এর উপর যথাক্রমে OD , OE এবং OF লম্ব টানা হল । 

প্রমাণ : ত্রিভুজ BOD এবং ত্রিভুজ BOE এর 

$\angle BDO = \angle BEO = {90^ \circ }$ ( অঙ্কনানুসারে )

$\angle OBE = \angle OBD$ ( যেহেতু OB , $\angle B$ এর অন্তর্সমদ্বিখণ্ডক )

এবং OB সাধারণ বাহু 

অতএব ত্রিভুজ BOD $\cong$ ত্রিভুজ BOE

অতএব OD = OE ( সর্বসম ত্রিভুজের অনুরূপ বাহু )

অনুরূপে প্রমাণ করা যায় ত্রিভুজ ত্রিভুজ COE $\cong$ ত্রিভুজ COF 

এবং OE = OF ( সর্বসম ত্রিভুজের অনুরূপ বাহু )

সুতরাং OD = OF 

এখন ত্রিভুজ AOD ও ত্রিভুজ AOF এর 

OD = OF 

OA সাধারণ বাহু 

এবং $\angle ADO = \angle AFO = {90^ \circ }$

অতএব ত্রিভুজ AOD $\cong$ ত্রিভুজ AOF

অতএব $\angle OAD = \angle OAF$ ( যেহেতু সর্বসম ত্রিভুজের অনুরূপ কোণ )

সুতরাং  AO হল $\angle A$ এর অন্তর্সমদ্বিখণ্ডক ।

অতএব প্রমাণিত যে ত্রিভুজের  অন্তর্সমদ্বিখণ্ডক তিনটি সমবিন্দু । 

 

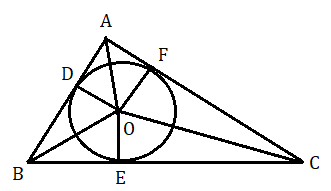
O কে কেন্দ্র করে OD এর সমান ব্যাসার্ধ নিয়ে অঙ্কিত বৃত্তকে ত্রিভুজ ABC এর অন্তর্বৃত্ত বলা যায়। OD কে অন্তর্বৃত্ত বলা হয় । OD কে অন্তর্ব্যাসার্ধ এবং বৃত্তের কেন্দ্র O কে অন্তঃকেন্দ্র বলা হয় ।

 

 

 

প্রয়োগ : প্রমাণ করতে হবে একটি ত্রিভুজের দুটি কোণের বহিঃসমদ্বিখণ্ডক এবং  একটি কোণের অন্তর্সমদ্বিখণ্ডক সমবিন্দু হবে । 

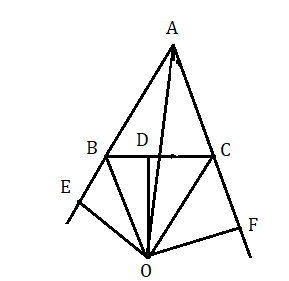ABC ত্রিভুজের $\angle ABC$ ও $\angle ACB$ এর বহিঃসমদ্বিখণ্ডক যথাক্রমে BO এবং CO , O বিন্দুতে পরস্পরকে ছেদ করেছে। A , O যুক্ত করা হল । 

প্রমাণ করতে হবে যে AO হল $\angle A$ এর অন্তর্সমদ্বিখণ্ডক । 

অঙ্কন : O বিন্দু থেকে BC , বর্ধিত AB এবং বর্ধিত AC এর উপর যথাক্রমে OD , OE এবং OF লম্ব টানা হল । 

প্রমাণ : ত্রিভুজ BOD ও ত্রিভুজ BOE এর মধ্যে 

$\angle OBD = \angle OBE$ ( যেহেতু OB হল $\angle B$ কোণের বহিঃসমদ্বিখণ্ডক )

OB সাধারণ বাহু 

$\angle BDO = \angle BEO = {90^ \circ }$ ( যেহেতু OD ও OE যথাক্রমে BC ও বর্ধিত AB বাহুর উপর লম্ব )

সুতরাং ত্রিভুজ BOD $\cong$  ত্রিভুজ BOE

OD = OE সর্বসম ত্রিভুজের অনুরূপ বাহু 

অনুরূপ ভাবে প্রমাণ করা যায় ত্রিভুজ COD $\cong$ ত্রিভুজ COF 

এবং OD = OF সর্বসম ত্রিভুজের অনুরূপ বাহু 

সুতরাং  OE = OF

এখন ত্রিভুজ AOE এবং ত্রিভুজ AOF এর 

$\angle AEO = \angle AFO = {90^ \circ }$ ( যেহেতু OD ও OE যথাক্রমে BC ও বর্ধিত AB বাহুর উপর লম্ব )

OE = OF

OA সাধারণ বাহু 

অতএব ত্রিভুজ AOE $\cong$ ত্রিভুজ AOF

অতএব $\angle OAE = \angle OAF$ অর্থাৎ AO হল $\angle A$ কোণের অন্তর্সমদ্বিখণ্ডক 

সুতরাং আমরা বলতে পারি ত্রিভুজের দুটি কোণের বহিঃসমদ্বিখণ্ডক এবং  একটি কোণের অন্তর্সমদ্বিখণ্ডক সমবিন্দু । 

 

ত্রিভুজের মধ্যমা তিনটি সমবিন্দু । 

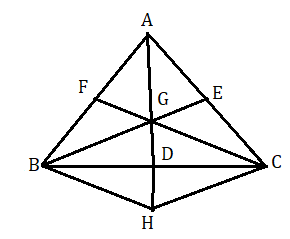মনে করি ABC একটি ত্রিভুজ এর BE ও CF মধ্যমা পরস্পরকে G বিন্দুতে ছেদ করেছে । A , G যুক্ত করে বর্ধিত করা হল। বর্ধিত AG , BC কে D বিন্দুতে ছেদ করেছে । 

আমাদের প্রমাণ করতে হবে D , BC বাহুর মধ্যবিন্দু। অর্থাৎ AD হল আর একটি মধ্যমা । 

অঙ্কন : AD কে H বিন্দু পর্যন্ত এমন ভাবে বর্ধিত করা হল যাতে AG = GH হয়। B , H ও C , H যুক্ত করা হল । 

প্রমাণ : এখন ত্রিভুজ ABH এর AB বাহুর মধ্যবিন্দু হল F

এবং AH বাহুর মধ্যবিন্দু হল G ( অঙ্কনানুসারে ) .

অতএব FG ।। BH 

সুতরাং GC ।। BH 

অনুরূপভাবে প্রমাণ করা যায় GB ।। CH 

এখন চতুর্ভুজ BGCH এর GC ।। BH এবং  GB ।। CH 

সুতরাং BGCH হল একটি সামান্তরিক 

BC ও GH হল BGCH সামান্তরিকের দুটি কর্ণ । 

সুতরাং BC ও GH পরস্পরকে D বিন্দুতে সমদ্বিখন্ডিত করবে । 

অতএব D হল BC এর মধ্যবিন্দু । 

সুতরাং ত্রিভুজের মধ্যমা তিনটি সমবিন্দু । 

যে বিন্দুতে ত্রিভুজের মধ্যমা তিনটি মিলিত হয়েছে তাকে ভরকেন্দ্র বলে । উপরের চিত্রে G বিন্দুতে ABC ত্রিভুজের তিনটি মধ্যমা মিলিত হয়েছে । তাই G কে ত্রিভুজ ABC এর ভরকেন্দ্র বলা হয় । 

 

কোনো ত্রিভুজের ভরকেন্দ্র তার মাধ্যমকে কি অনুপাতে বিভুক্ত করে । 

মনে করি ABC ত্রিভুজের তিনটি মধ্যমা AD , BE ও CF পরস্পরকে G বিন্দুতে ছেদ করেছে । 

AG : GD কি হবে তা আমাদের নির্ণয় করতে হবে । 

অঙ্কন : AD কে H বিন্দু পর্যন্ত এমন ভাবে বর্ধিত করা হল যাতে AG = GH হয়। B , H ও C , H যুক্ত করা হল । 

আমরা পূর্বেই প্রমাণ করেছি BGCH হল একটি সামান্তরিক 

BC ও GH হল BGCH সামান্তরিকের দুটি কর্ণ । 

সুতরাং BC ও GH পরস্পরকে D বিন্দুতে সমদ্বিখন্ডিত করবে । 

সুতরাং D হল GH এর মধ্যবিন্দু । 

অতএব 

$\begin{array}{l} AG:GD\\  = \frac{{AG}}{{GD}}\\  = \frac{{AG}}{{\frac{1}{2}GH}}\\  = \frac{{AG}}{{\frac{1}{2}AG}}\\  = 2\\  \Rightarrow AG:GD = 2:1 \end{array}$

 

একটি ত্রিভুজের দুটি মধ্যমা সমান হলে ত্রিভুজটি সমদ্বিবাহু ত্রিভুজ হবে। 

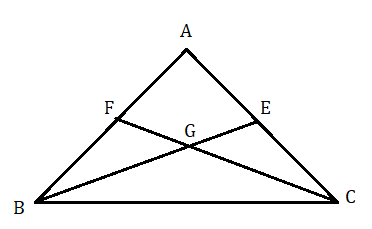মনে করি ABC একটি ত্রিভুজ যার CF এবং BE দুটি মধ্যমা সমান । 

আমাদের প্রমাণ করতে হবে যে ABC ত্রিভুজটি হল সমদ্বিবাহু ত্রিভুজ। 

প্রমাণ : মনে করি BE ও CF দুটি মধ্যমা পরস্পরকে G বিন্দুতে ছেদ করেছে ।

অতএব $GE = \frac{1}{3}BE$ এবং $GF = \frac{1}{3}CF$

যেহেতু BE = CF 

অতএব GE = GF এবং BG = CG 

এখন ত্রিভুজ FGB এবং ত্রিভুজ EGC এর মধ্যে 

GE = GF

BG = CG

এবং $\angle FGB = \angle EGC$

ত্রিভুজ FGB $\cong$ ত্রিভুজ EGC

সুতরাং BF = CE ( সর্বসম ত্রিভুজের অনুরূপ বাহু )

অতএব 2BF = 2CE $\Rightarrow$ AB = AC

সুতরাং ABC একটি সমদ্বিবাহু ত্রিভুজ 

 

ABC ত্রিভুজের তিনটি মধ্যমা AD , BE ও CF পরস্পরকে G বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে 

(i) ত্রিভুজ GBC = $\frac{1}{3}$ত্রিভুজ ABC  (ii) ত্রিভুজ GBD = $\frac{1}{6}$ত্রিভুজ ABC 

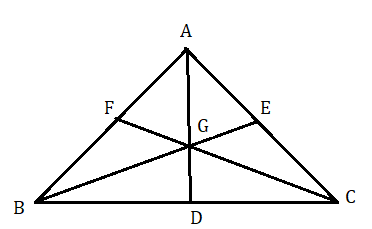ABC ত্রিভুজের তিনটি মধ্যমা AD , BE ও CF পরস্পরকে G বিন্দুতে ছেদ করেছে ।

প্রমাণ করতে হবে যে 

(i) ত্রিভুজ GBC = $\frac{1}{3}$ত্রিভুজ ABC  (ii) ত্রিভুজ GBD = $\frac{1}{6}$ত্রিভুজ ABC

প্রমাণ : AD হল ABC ত্রিভুজের মধ্যমা 

অতএব ত্রিভুজ ABD = ত্রিভুজ ACD ..........(i) ( যেহেতু ত্রিভুজের মধ্যমা ত্রিভুজকে সমান ক্ষেত্রফল বশিষ্ট দুটি ত্রিভুজে বিভক্ত করে )

আবার GD হল GBC ত্রিভুজের মধ্যমা 

অতএব ত্রিভুজ GBD = ত্রিভুজ GCD ...............(ii) ( যেহেতু ত্রিভুজের মধ্যমা ত্রিভুজকে সমান ক্ষেত্রফল বশিষ্ট দুটি ত্রিভুজে বিভক্ত করে )

এখন (i) - (ii) করে পাই 

ত্রিভুজ ABD -  ত্রিভুজ GBD =  ত্রিভুজ ACD - ত্রিভুজ GCD

ত্রিভুজ AGB = ত্রিভুজ AGC 

অনুরূপভাবে প্রমাণ করা যায় ত্রিভুজ ত্রিভুজ AGB = ত্রিভুজ BGC 

ত্রিভুজ AGB = ত্রিভুজ AGC = ত্রিভুজ BGC = $\frac{1}{3}$(ত্রিভুজ AGB + ত্রিভুজ AGC + ত্রিভুজ BGC) = $\frac{1}{3}$ত্রিভুজ ABC

আবার ত্রিভুজ GBD = $\frac{1}{2}$ ত্রিভুজ GBC ( যেহেতু GD ত্রিভুজ GBC এর মধ্যমা )

অতএব ত্রিভুজ GBD = $\frac{1}{2}$ ( $\frac{1}{3}$ত্রিভুজ ABC ) = $\frac{1}{6}$ত্রিভুজ ABC

*****