লম্ব-বৃত্তাকার শঙ্কু (Right-circular Cone)
সংজ্ঞা (Definition) কোনো সমকোণী ত্রিভুজের সমকোণ ধারক যেকোনো একটি বাহুকে স্থির রেখে বা অক্ষ ধরে ত্রিভুজটিকে একবার পূর্ণ আবর্তন করালে যে ঘনবস্তু উৎপন্ন হয় , তাকে শঙ্কু বলে ।
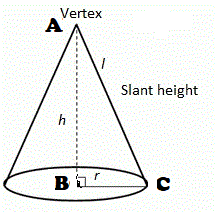
উপরের চিত্রে △ABC ত্রিভুজ এর [tex]\angle B[/tex] হল একটি সমকোণ । AB কে অক্ষ ধরে ত্রিভুজটিকে একবার আবর্তন করায় শঙ্কুটি উৎপন্ন হয়েছে । AC কে শঙ্কু টির উৎপাদক রেখা (Generating line) বলা হয় । A কে শঙ্কুটির শীর্ষ (Vertex) বলা হয় । C বিন্দু দ্বারা গঠিত বৃত্তাকার ক্ষেত্রটিকে শঙ্কুর ভূমি (Base) বলে । BC বৃত্তের ব্যাসার্ধ । বৃত্তাকার ভূমির উপর লম্ব AB কে শঙ্কুর উচ্চতা (Height) বলা হয় এবং AC কে শঙ্কুর তির্যক উচ্চতা (Slant height) বলা হয় ।
শঙ্কুর দুটি তল (১) একটি বৃত্তাকার সমতল, (২) একটি বক্রতল -যাকে শঙ্কুর পার্শ্বতল বলে । বাস্তবক্ষেত্রে আমরা যেসব শঙ্কুর আকৃতির ঘনবস্তু দেখতে পাই তা হল রাজমিস্তিরির ওলন, মোচার অগ্রভাগ, ফানেল, টোপর ইত্যাদি ।
শঙ্কুর ক্ষেত্রফল ও আয়তন নির্ণয় :-
মনে করি শঙ্কুর ভূমির ব্যাসার্ধ হল r, উচ্চতা h এবং তির্যক উচ্চতা l হলে, তার
(1) পার্শ্বতলের ক্ষেত্রফল
= [tex]\pi rl[/tex] = [tex]\pi [/tex] [tex] \times [/tex] ভূমির ব্যাসার্ধ [tex] \times [/tex] তির্যক উচ্চতা
= [tex]\frac{1}{2} \times [/tex] ভূমির পরিধি [tex] \times [/tex] তির্যক উচ্চতা
(2) সমগ্রতলের ক্ষেত্রফল
= ভূমির ক্ষেত্রফল + পার্শ্বতলের ক্ষেত্রফল
[tex]\begin{array}{l}
= \pi {r^2} + \pi rl\\
= \pi r\left( {r + l} \right)
\end{array}[/tex]
(3) আয়তন বা ঘনফল
= [tex]\frac{1}{3}[/tex] [tex] \times [/tex] ভূমির ক্ষেত্রফল [tex] \times [/tex] উচ্চতা
[tex] = \frac{1}{3}\pi {r^2}h[/tex]
(4) তির্যক উচ্চতা ( l )[tex] = \sqrt {{r^2} + {h^2}} [/tex]