স্থানাঙ্ক জ্যামিতি : দূরত্ব নির্ণয় (Co-ordinate Geometry : Distance formula)
সূচনা (Introduction)
আমরা graph কাগজে যেমন বিভিন্ন বিন্দুকে স্থাপন করতে পারি তেমনি ওই বিন্দু গুলির সাহায্যে বিভিন্ন জ্যামিতিক চিত্র , সরলরেখা অঙ্কন করা যায় । দেখা যাচ্ছে বিন্দু গুলির স্থানাঙ্ক জানা থাকলে সেগুলি যোগ করে বিভিন্ন সমতলিক জ্যামিতিক চিত্র পাওয়া যায় । আবার বিভিন্ন বীজগাণিতিক দুই চল বিশিষ্ট রৈখিক সমীকরণের জ্যামিতিক আকার সম্মন্ধে ঠিক মতো ধারণা করা যায় ।
এইভাবে বীজগণিতের সাহায্যে বিভিন্ন জ্যামিতিক আকারের ধারণা গড়ে ওঠাকে স্থানাঙ্ক জ্যামিতি (Co-ordinate Geometry) বলা হয় ।
অর্থাৎ স্থানাঙ্ক জ্যামিতিতে বীজগণিতের সাহায্যে জ্যামিতির ধারণা করতে পারি
তাই স্থানাঙ্ক জ্যামিতি ব্যাপকতরভাবে বিজ্ঞানের বিভিন্ন শাখায় ব্যবহার করা হয় ।
মূলবিন্দু (0,0) থেকে অক্ষরেখার উপরে অবস্থিত যেকোনো বিন্দুর স্থানাঙ্ক নির্ণয়
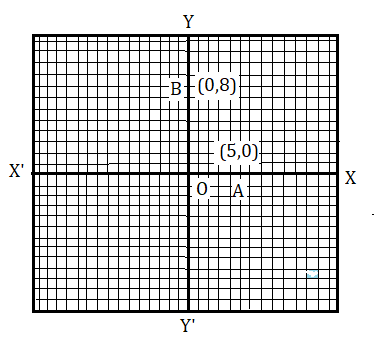
এখানে দুটি লম্ব অক্ষ হল XOX' ও YOY' এবং O(0,0) হল মূলবিন্দু .
এখানে A(5,0) ও B(0,8) দুটি বিন্দু । আমরা পরিষ্কারভাবে বলতে পারি A ও B বিন্দু দুটি মূলবিন্দু থেকে যথাক্রমে 5 একক ও 8 একক দূরত্বে অবস্থিত । সুতরাং x অক্ষের উপরে অবস্থিত যেকোনো বিন্দুর স্থানাঙ্ক তার ভুজের ধনাত্মক মান । অনুরূপে y অক্ষের উপরে অবস্থিত যেকোনো বিন্দুর স্থানাঙ্ক হবে কোটির ধনাত্মক মান ।
লম্ব অক্ষের উপর অবস্থিত যেকোনো দুটি বিন্দুর দূরত্ব নির্ণয়
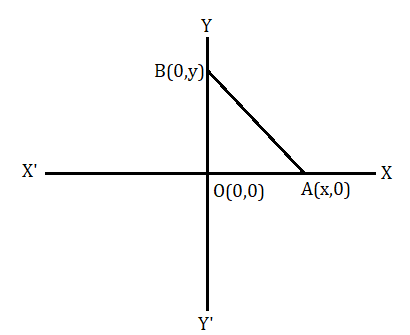 মনে করি A(x,0) ও B(0,y) দুটি বিন্দু যথাক্রমে x অক্ষ ও y অক্ষের উপরে অবস্থিত ।
মনে করি A(x,0) ও B(0,y) দুটি বিন্দু যথাক্রমে x অক্ষ ও y অক্ষের উপরে অবস্থিত ।
মূলবিন্দু থেকে A বিন্দুর দূরত্ব হল x একক অর্থাৎ OA = x একক
অনুরূপে মূলবিন্দু থেকে B বিন্দুর দূরত্ব হল y একক অর্থাৎ OB = y একক
এখন পিথাগোরাসের উপপাদ্য ব্যবহার করে পাই
(AB)2=(OA)2+(OB)2⇒AB=√(OA)2+(OB)2=√x2+y2
উদাহরণ : রোহিত x অক্ষের উপরে একটি বিন্দু M(6,0) এবং y অক্ষের উপরে একটি বিন্দু N(0,8) নিয়েছে । এখন MN এর দৈর্ঘ্য নির্ণয় করে দেখি ।
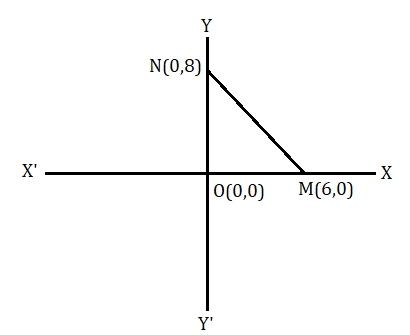 M বিন্দুর স্থানাঙ্ক (6,0) এবং N বিন্দুর স্থানাঙ্ক (0,8)
M বিন্দুর স্থানাঙ্ক (6,0) এবং N বিন্দুর স্থানাঙ্ক (0,8)
অতএব OM = 6 একক এবং ON = 8 একক
অতএব
MN=√62+82=√36+64=√100=10
অতএব MN = 10 একক ।
মূলবিন্দু থেকে যেকোনো বিন্দুর দূরত্ব নির্ণয়
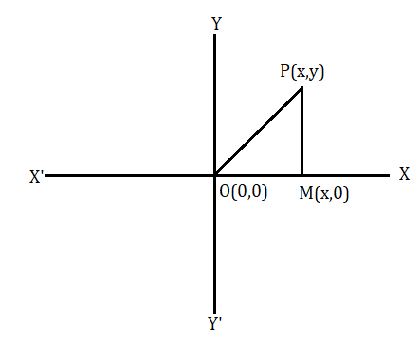 মনে করি P(x,y) যেকোনো বিন্দু। মূলবিন্দু O(0,0) থেকে এর দূরত্ব নির্ণয় করতে হবে ।
মনে করি P(x,y) যেকোনো বিন্দু। মূলবিন্দু O(0,0) থেকে এর দূরত্ব নির্ণয় করতে হবে ।
P(x,y) বিন্দু থেকে x অক্ষের উপর PM লম্ব টানা হল। অতএব M এর স্থানাঙ্ক হবে (x,0) .
এখন OM = x একক এবং PM = y একক ।
পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই
OP2=OM2+PM2⇒OP=√OM2+PM2=√x2+y2
মূলবিন্দু থেকে P(x,y) বিন্দুর দূরত্ব হল √x2+y2 একক ।
উদাহরণ : মূলবিন্দু থেকে (3,4) বিন্দুর দূরত্ব নির্ণয় করো
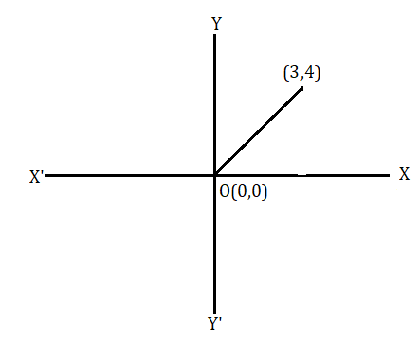 মূলবিন্দু থেকে (3,4) বিন্দুর দূরত্ব
মূলবিন্দু থেকে (3,4) বিন্দুর দূরত্ব
=√32+42 একক
=√9+16 একক
=√25 একক
= 5 একক
যেকোনো দুটি বিন্দুর মধ্যবর্তী দূরত্ব নির্ণয়
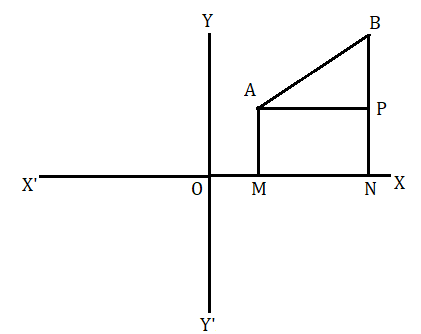 মনে করি A ও B দুটি বিন্দুর স্থানাঙ্ক হল যথাক্রমে (x1,y1) এবং (x2,y2) .
মনে করি A ও B দুটি বিন্দুর স্থানাঙ্ক হল যথাক্রমে (x1,y1) এবং (x2,y2) .
আমাদের A ও B বিন্দু দুটির মধ্যবর্তী দূরত্ব নির্ণয় করতে হবে ।
A ও B বিন্দু থেকে x অক্ষের উপরে দুটি লম্ব যথাক্রমে AM ও BN অঙ্কন করা হল ।
A বিন্দু থেকে BN এর উপর AP লম্ব অঙ্কন করলাম ।
A ও B দুটি বিন্দুর স্থানাঙ্ক হল যথাক্রমে (x1,y1) এবং (x2,y2) .
অতএব OM=x1 এবং ON=x2
AM=y1 এবং BN=y2
AP = MN = ON - OM = x2−x1
এবং BP = BN - PN = BN - AM = y2−y1
অতএব সমকোণী ত্রিভুজ ABP তে পিথাগোরাগের উপপাদ্য প্রয়োগ করে পাই
AB=√AP2+BP2=√(x2−x1)2+(y2−y1)2
অতএব A(x1,y1) ও B(x2,y2) বিন্দুদ্বয়ের মধ্যবর্তী দূরত্ব হল
√(x2−x1)2+(y2−y1)2 একক .
উদাহরণ : (2,4) ও (5,7) বিন্দুর দূরত্ব নির্ণয় করো
এখানে x1=2 , y1=4 , x2=5 এবং y2=7
অতএব নির্ণেয় দূরত্ব
=√(5−2)2+(7−4)2 একক
=√32+32 একক
=√9+9 একক
=√18 একক
=9√2 একক
*****