বিভিন্ন প্রকার রাশিমালা (Different types of Expression)
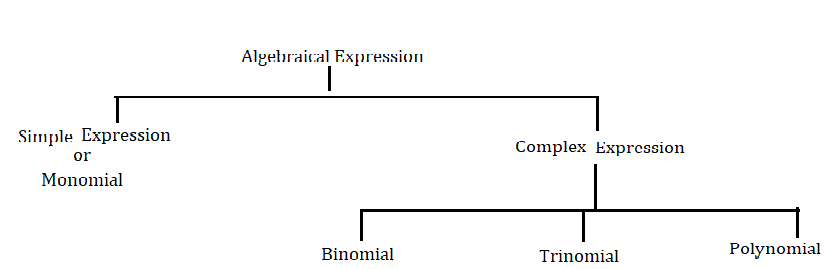
বীজগাণিতিক রাশিমালা ( Algebraical Expression ) দুইপ্রকার
- সরল রাশি ( Simple Expression ) বা এক পদীয় ( Monomial )
- জটিল রাশি ( Complex Expression )
জটিল রাশি ( Complex Expression ) আবার তিন প্রকার
- দ্বিপদরাশি ( Binomial )
- ত্রিপদরাশি ( Trinomial )
- বহুপদীয় রাশি ( Polynomial )
সরল রাশি ( Simple Expression ) বা এক পদীয় ( Monomial ) : কোনো বীজগাণিতিক রাশিমালাতে কেবলমাত্র একটি পদ থাকলে তাকে সরল রাশি বলে । যেমন , [tex]2x[/tex] , [tex]a \div b[/tex] , [tex]\frac{{4a \times 5c}}{b}[/tex] ইত্যাদি ।
দ্বিপদরাশি ( Binomial ) : দুই পদযুক্ত রাশিমালাকে দ্বিপদরাশি (Binomial) বলে । যেমন , [tex]a + x[/tex] , [tex]2{x^2} + 3[/tex] , [tex]5\frac{x}{y} - {x^3}[/tex] ইত্যাদি ।
ত্রিপদরাশি ( Trinomial ) : কোনো রাশিমালাতে তিনটি পদ থাকলে তাকে ত্রিপদরাশি (Trinomial) বলে । যেমন , [tex]a + b + c[/tex] , [tex]{x^4} + 5{y^2} - z[/tex] , [tex]2x - 3\frac{y}{z} + {x^3}[/tex] ইত্যাদি ।
বহুপদীয় রাশি ( Polynomial ) : তিনটির বেশি পদ বিশিষ্ট রাশিমালাকে বহুপদীয় রাশি (Polynomial) বলে । যেমন , [tex]{x^3} + 3xy - z + 5x{y^2}[/tex] , [tex]5{z^2} + 3{y^2} - {x^3}{z^3} - {y^4}xz + 7xyz[/tex] ইত্যাদি ।
মনে রাখতে হবে 8 , 1 , -5 , 10 ইত্যাদি এরাও কিন্তু বহুপদী সংখ্যামালা এদেরকে ধ্রূবক বহুপদী সংখ্যামালা (Constant Polynomial) বলে । কিন্তু (0) শূন্য কে শূন্য বহুপদী সংখ্যামালা (Zero Polynomial) বলে ।
অপেক্ষক এবং চলমানরাশি ( Function and Variables ) :
কোনো বর্ণ দিয়ে প্রকাশিত বীজগাণিতিক রাহিমালাকে ওই বর্ণের অপেক্ষক বলা হয় এবং ওই বর্ণটিকে ওই অপেক্ষকের চলমান রাশি বলা হয় । অর্থাৎ অপেক্ষক নির্ণয়কারী বর্ণকেই চলমান রাশি বলা হয় ।
যেমন , [tex]{x^2} + 2x + 1[/tex] এই রাশিকে x এর অপেক্ষক বলা হয় । আবার x হল এই অপেক্ষকের চলরাশি ।
[tex]{x^3} + 3{x^2}y - 3x{y^2}[/tex] এই রাশিকে x এবং y এর অপেক্ষক বলা হয় । আবার x এবং y হল এই অপেক্ষকের চলরাশি ।
অপেক্ষক সাধারণত প্রকাশ করা হয় [tex]f\left( x \right),g\left( x \right),\phi \left( x \right),\psi \left( x \right)[/tex] , [tex]f\left( {x,y} \right)[/tex]ইত্যাদি সংকেত দ্বারা ।
অপেক্ষক প্রধাণত দুই প্রকার হয়
- অখন্ড অপেক্ষক ( Integral function )
- মূলদ অপেক্ষক ( Rational function )
অখন্ড অপেক্ষক ( Integral function ) : যে অপেক্ষকের চলরাশিগুলি হরে অবস্থান করে না তাকে অখন্ড অপেক্ষক বলে। যেমন [tex]{x^2} + 2x + 3[/tex]
মূলদ অপেক্ষক ( Rational function ) : যে অপেক্ষকের চলরাশিগুলির সূচক ভগ্নাংশ হয় না তাকে মূলদ অপেক্ষক বলে। যেমন [tex]{x^3} + 2{x^2} + 3y[/tex] , [tex]5{x^4} + 6x - 3{y^2}[/tex]
বহুপদীয় রশির ঘাত হল প্রদত্ত চলরাশিগুলির সর্বোচ্চ ঘাত বা মাত্রা ( degree )।
যেমন [tex]f\left( x \right) = 5{x^3} - 3x + 8[/tex] এই বহুপদী সংখ্যামালার মাত্রা হল 3 . আবার [tex]g\left( x \right) = 5{x^{15}} - 3{x^2} + 8[/tex] এই বহুপদী সংখ্যামালার মাত্রা হল 15 .
শূন্য ছাড়া যেকোনো বহুপদী সংখ্যামালার মাত্রা 0 . যেমন [tex]8 = 8{x^0}[/tex] , [tex] - 5 = - 5{x^0}[/tex] . কিন্তু শূন্য বহুপদী সংখ্যামালার মাত্রা অসংজ্ঞাত। যেহেতু [tex]0 = 0{x^0}[/tex] , [tex]0 = 0{x^{10}}[/tex] ।
*****









