জটিল রাশি (Complex Number)
ভূমিকা (Introduction)
আমরা এর আগে বাস্তব সংখ্যা (Real Number) সম্পর্কে জ্ঞান লাভ করেছি । প্রকৃতপক্ষে সকল মূলদ ও অমূলদ সংখ্যার সমষ্টিকে বাস্তব সংখ্যা বলে । বাস্তব সংখ্যার অন্যতম বৈশিষ্ট হল যে তাদের বর্গ করলে বর্গফল সর্বদা ধনাত্মক হবে । যেমন 3, 45 , -2 , √2 ইত্যাদি এই সমস্ত সংখ্যার বর্গ করলে হয় যথাক্রমে 9, 1625, 4, 2 . এরা সবই ধনাত্মক সংখ্যা । অতএব কোনো রাশির বর্গের মান যখন ঋণাত্মক হয়, তখন তাকে বাস্তব সংখ্যা বলা যায় না । যেমন √−2,√−5 ইত্যাদি , এই সমস্ত সংখ্যা গুলির বর্গ করলে বর্গফল হয় ঋণাত্মক । এই সমস্ত সংখ্যাকে বাস্তব সংখ্যা বলা যায় না । এইরূপ ভিন্ন সংখ্যাকে জটিল রাশি (Complex Number) বা অবাস্তব বা কাল্পনিক সংখ্যা (Imaginary Number) বলা হয় ।
►জটিল রাশি (Complex Number)
দুটি বাস্তব রাশি x এবং y এর ক্রমযুগল ( x , y ) যদি x + i y ( যেখানে i=√−1 )আকারে প্রকাশ করা হয় , তবে (x , y) ক্রমযুগলকে জটিল রাশি বা কাল্পনিক সংখ্যা (Complex Number or Imaginary Number) বলে ।
সংজ্ঞানুযায়ী যদি ( x , y ) কে z দ্বারা প্রকাশ করা হয়, তবে z = ( x , y ) = x + i y হবে । যদি y = 0 হয় তাহলে z = ( x , 0 ) = x + i.0 = x এক্ষেত্রে জটিল রাশি একটি বিশুদ্ধ বাস্তব সংখ্যা হয় । অতএব দেখা যাচ্ছে যে বাস্তব সংখ্যাশ্রেণী হল জটিল রাশির একটি অংশ । আবার যখন x = 0 , তখন z = ( 0 , y ) = i.y হয় । এটি বিশুদ্ধ জটিল সংখ্যা । আবার যখন x = 0 এবং y = 1 হয় ,তখন z = ( 0 , 1 ) = i হয়। এই জন্য z = ( x , y ) জটিল রাশির x কে বাস্তব অংশ ও y কে অবাস্তব অংশ বলে ।
►অনুবন্দী বা প্রতিযোগী জটিল রাশি (Conjugate Complex Number)
x , y বাস্তব সংখ্যা এবং i=√−1 হলে ( x + i.y ) ও (x - i.y )দুটি জটিল রাশিকে একে অপরের প্রতিযোগী বা অনুবন্দী জটিল রাশি (Conjugate Complex Number) বলে । z একটি প্রদত্ত জটিল রাশি হলে ˉz হল তার অনুবন্দী বা প্রতিযোগী জটিল রাশি । যেমন 2+3i এর অনুবন্দি জটিল রাশি হল 2−3i । সুতরাং z=2+3i হলে ˉz=2−3i হবে ।
দ্রষ্টব্য :
(1) z ও ˉz দুটি পরস্পর অনুবন্দি জটিল রাশি হলে দেখাও যে ¯¯zহবে ।
প্রমাণ :- মনে করি z=x+iy অতএব ˉz=x−iy .
এখন ˉz=x−iy এর অনুবন্দি জটিল রাশি হবে x + iy .
সুতরাং ˉz এর অনুবন্দি জটিল রাশি হল ¯¯z=x+iy .
(2) যেকোন জটিল রাশি x + iy এর অনবন্দি জটিল রাশির আকার হবে x - iy . অর্থাৎ i = -i হবে ।
(3) z=x+iy হলে ওর অনুবন্দি জটিল রাশি হবে ˉz=x−iy .
z+ˉz=x+iy+x−iy=2x একটি বাস্তব সংখ্যা ।
z−ˉz=x+iy−x+iy=2iy একটি কাল্পনিক সংখ্যা ।
z⋅ˉz=(x+iy)⋅(x−iy)=x2−(√−1)2y2=x2+y2 একটি বাস্তব সংখ্যা ।
যেহেতু (i=√−1) .
(4) মনে করি z1=x1+iy1,z2=x2+iy2 .
অতএব উহাদের অনুবন্দি জটিল রাশি হল যথাক্রমে ¯z1=x1−iy1,¯z2=x2−iy2 .
এখন z1+z2=x1+iy1+x2+iy2=(x1+x2)+i(y1+y2).
¯z1+z2=(x1+x2)−i(y1+y2)=x1−iy1+x2−iy2=¯z1+¯z2
অনুরূপে আমরা প্রমাণ করতে পারি
¯z1−z2=¯z1−¯z2;¯z1z2=¯z1⋅¯z2;¯(z1z2)=¯z1¯z2
►জটিল রাশির মডিউলাস ও অ্যামপ্লিচিউড বা আরগুমেন্ট (Modulus and Amplitude or Argument of a Complex Number)
1. জটিল রাশির মডিউলাস :
মনে করি z=x+iy , যেখানে x , y হল বাস্তব এবং i=√−1 তাহলে , (x2+y2) এর ধনাত্মক বর্গমূলকে z জটিল রাশির মডিউলাস হয় এবং একে mod(z) বা mod z বা ।z। প্রতীক দ্বারা প্রকাশ করা হয়। সুতরাং z=x+iy হলে
|z|=modz=+√x2+y2
যদি z = 0 হয় অর্থাৎ x = y = 0 হয় তবে ।z। = 0 হবে। যেকোনো জটিল রাশি z এর ক্ষেত্রে |z|=|¯z|=|−z| .
2. জটিল রাশির অ্যামপ্লিচিউড বা আরগুমেন্ট :
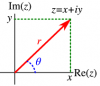
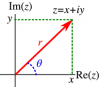
মনে করি z=x+iy , যেখানে x , y হল বাস্তব এবং i=√−1 , x2+y2≠0 তাহলে θ এর যেকোনো মান দ্বারা আমরা x এবং y কে প্রকাশ করতে পারি। যেখানে
x=|z|cosθ......(i)
y=|z|sinθ......(ii)
এই দুটি সমীকরণকে z জটিল রাশির অ্যামপ্লিচিউড বা আরগুমেন্ট বলে ।
স্পষ্টতই , θ এর অসংখ্য মানের জন্য সমীকরণ (i) এবং (ii) সিদ্ধ হয় , এই কারণে প্রদত্ত জটিল রাশি z=x+iy এর অসংখ্য মান পাওয়া। এই সকল মানের মধ্যে θ এর যে মান −π<θ≤π এর মধ্যে থাকে তাকে z জটিল রাশির আরগুমেন্টের মুখ্যমান (Principal value) বলে । এই মানকে argz প্রতীক দ্বারা প্রকাশ করা হয় ।
- 7227 views