বাস্তব সংখ্যা (Real Number)
স্বাভাবিক সংখ্যা ( Natural Number ) : যে সমস্ত সংখ্যা দিয়ে কোনো বস্তু গণনা করা হয়, সেগুলি হল স্বাভাবিক সংখ্যা । স্বাভাবিক সংখ্যা গুলিকে ধনাত্মক পূর্ণ সংখ্যা বলে। যেমন 1 , 2 , 3 , 4 ,...............ইত্যাদি । স্বাভাবিক সংখ্যার মধ্যে সবচেয়ে ছোট হল 1. স্বাভাবিক সংখ্যার সেটকে সাধারণ ভাবে N চিহ্ন দিয়ে প্রকাশ করা হয়। সুতরাং
N = { 1 , 2 , 3 , ..............65 , ..........135 , ...............} . এই সংখ্যার সেট থেকে দেখা যাচ্ছে স্বাভাবিক সংখ্যার মধ্যে সবচেয়ে বড়ো সংখ্যাটি কল্পনা করা যায় না ।
উপরের বৃত্তের মধ্যে স্বাভাবিক সংখ্যার দলকে দেখানো হয়েছে । দুটি স্বাভাবিক সংখ্যা যোগ করলে একটি স্বাভাবিক সংখ্যা পাওয়া যায়। যেমন 1 + 2 = 3 , 3 + 4 = 7 , 3 + 4 + 5 = 12 ইত্যাদি । দুই এর বেশি স্বাভাবিক সংখ্যা যোগ করলেও একটি স্বাভাবিক সংখ্যা পাওয়া যায় ।
একই ভাবে দুটি এর বেশি স্বাভাবিক সংখ্যা গুণ করলেও স্বাভাবিক সংখ্যা পাওয়া যায় । সুতরাং যোগ ও গুণের সাপেক্ষে স্বাভাবিক সংখ্যা বদ্ধ । কিন্তু দুটি স্বাভাবিক সংখ্যার বিয়োগফল সবসময় একটি স্বাভাবিক সংখ্যা নাও হতে পারে । যেমন 3 - 2 = 1 এটি স্বাভাবিক সংখ্যা কিন্তু 2 - 4 = -2 এটি স্বাভাবিক সংখ্যা নয় ।
একইভাবে দুটি স্বাভাবিক সংখ্যার ভাগফল সর্বদা স্বাভাবিক সংখ্যা নাও হতে পারে । যেমন 42=2 এটি একটি স্বাভাবিক সংখ্যা কিন্তু 64=32 এটি স্বাভাবিক সংখ্যা নয় ।
স্বাভাবিক সংখ্যার ধর্ম
উপরের আলোচনা থেকে স্বাভাবিক সংখ্যার যে ধর্ম গুলি পাই তা হল
- a + b = b + a [ যোগের বিনিময় নিয়ম ]
- ( a + b ) + c = a + ( b + c ) [ যোগের সংযোগ নিয়ম ]
- ab = ba [ গুণের বিনিময় নিয়ম ]
- (ab) c = a (bc) [ গুণের সংযোগ নিয়ম ]
- a ( b+ c ) = ab + ac অতএব ( a + b ) c = ac + bc [ বিচ্ছেদ নিয়ম ]
এখানে a , b এবং c হল স্বাভাবিক সংখ্যা। সুতরাং স্বাভাবিক সংখ্যা বিনিময় , সংযোগ ও বিচ্ছেদ নিয়ম সিদ্ধ ।
'0' কি স্বাভাবিক সংখ্যা ?
'0' স্বাভাবিক সংখ্যা নয় । কেবল শূন্য দিয়ে কোনো বস্তু গণনা করা যায় না । কোনো সংখ্যাকে শূন্য দিয়ে যোগ করলে সেই সংখ্যার কোনো পরিবর্তন হয় না । বিপরীতভাবে শূন্যের সঙ্গে কোনো সংখ্যা যোগ করলে সেই সংখ্যাটি পাওয়া যায় । যেমন 2 + 0 = 2 , 0 + 5 = 5 ইত্যাদি ।
কোনো সংখ্যা থেকে শূন্য বিয়োগ করলে সেই সংখ্যাটি পাওয়া যায় । কিন্তু শূন্য থেকে কোনো সংখ্যা বিয়োগ করলে সেই সংখ্যাটি ধনাত্মক থেকে ঋণাত্মক হয়ে যায় । 2 - 0 = 2 , 6 - 0 = 6 , 0 - 4 = -4 , 0 - 7 = -7 ইত্যাদি ।
যেকোনো সংখ্যাকে শূন্য দিয়ে গুণ করলে শূন্য হয় । অনুরূপভাবে শূন্য কে কোনো সংখ্যা দিয়ে গুণ করলেও শূন্য হয় । যেমন 2×0=0 , 7×0=0 , 0×5=0 ইত্যাদি ।
শূন্য কে যেকোনো সংখ্যা দ্বারা ভাগ করলে ভাগফল শূন্য পাওয়া যায় । কিন্তু শূন্য দিয়ে কোনো সংখ্যাকে ভাগ করা যায় না । কারণ শূন্য দিয়ে কোনো সংখ্যাকে ভাগ করলে তার মান হয় অর্থহীন । যেমন 0÷2=0 , 0÷6=0 , 6÷0=60 অর্থহীন , 2÷0=20 অর্থহীন ইত্যাদি ।
উপরের আলোচনা থেকে দেখা যাচ্ছে শূন্য স্বাভাবিক সংখ্যার ধর্ম গুলিকে সিদ্ধ করে না ।
শূন্যের এই গাণিতিক গুণাবলী সূত্রাকারে লিপিবদ্ধ করলে হয় ,
- a + 0 = a
- 0 + a = a
- 0 + 0 = 0
- a - 0 = 0
- 0 - a = -a
- a×0=0
- 0×a=0
- 0×0=0
মনে রাখতে হবে শূন্যই একমাত্র পূর্ণসংখ্যা যা ধনাত্মক বা ঋণাত্মক কোনোটিই নয় ।
অখন্ড সংখ্যা ( Whole number ) : শূন্য ( 0 ) এবং সমস্ত স্বাভাবিক সংখ্যাকে অখন্ড সংখ্যা বলে। এই সংখ্যা গুলি হল 0 , 1 , 2 , 3 , ............. ইত্যাদি। যেকোনো অখন্ড সংখ্যার সাথে 1 যোগ করলে পরবর্তী অখন্ড সংখ্যা পাওয়া যায়। অখন্ড সংখ্যার সেট কে W চিহ্ন দিয়ে প্রকাশ করা হয় । অতএব
W = { 0 , 1 , 2 , 3 , .................100 , ...........225 ,.............}
সংখ্যা অক্ষ ( Number axis )
ধরা যাক AB একটি সরলরেখা এবং এই সরলরেখার জ্যামিতিক নিয়মে স্বাভাবিক দুটি দিককে যথেচ্ছ বাড়ানো যায় । এই সরলরেখার উপরে যেকোনো একটি বিন্দু নেওয়া হল । এই বিন্দুটিকে মূলবিন্দু ( Origin ) 0 বলে চিহ্নিত করা হল । এই বিন্দুটিকে শূন্য সংখ্যার অবস্থান বলে কল্পনা করা হয়। এবার একটি নির্দিষ্ট দৈঘ্যকে এক একক ( Unit distance ) ধরে নিয়ে , 0 বিন্দুর ডানদিকে একক দৈর্ঘ্য ঐ সরলরেখার উপরে যে বিন্দু পাওয়া যায় সেখান 1 এবং অনুরূপভাবে বাঁদিকে একক দৈর্ঘ্য দূরে সরলরেখাটির উপরের বিন্দুটিকে -1 ধরা হয় ।
একইরকমভাবে 1 চিহ্নিত বিন্দুর ডানদিকে একক দৈর্ঘ্য ঐ সরলরেখার উপরে যে বিন্দু পাওয়া যায় সেখান 2 এবং -1 চিহ্নিত বিন্দুর বাঁদিকে একক দৈর্ঘ্য দূরে সরলরেখাটির উপরের বিন্দুটিকে -2 ধরা হয় ।
এইভাবে অন্তহীনভাবে চালিয়ে গেলে আমরা যে অক্ষ পাব তাকে সংখ্যা অক্ষ বলে ।
আমরা সংখ্যা সারিটি দেখলে পাব
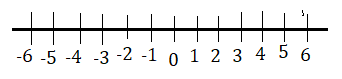
পূর্ণসংখ্যা ( Integer ) : অখন্ড সংখ্যা ও 0 , -1 , -2 , -3 , ............ সংখ্যা মিলিত হয়ে যে সংখ্যার দল বা সংখ্যার সেট তৈরি করে তাকে পূর্ণসংখ্যা বলে। পূর্ণসংখ্যার দলকে সাধারণ ভাবে Z চিহ্ন দ্বারা প্রকাশ করা হয় । অতএব
Z = { .................-5 , -4 , -3 , -2 , -1 , 0 , 1 , 2 , 3,.................}
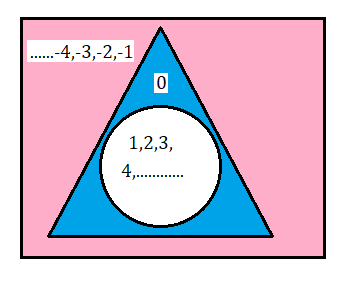
0 অপেক্ষা বড়ো সংখ্যা গুলিকে ধনাত্মক পূর্ণসংখ্যা ( Positive Integer ) ও 0 অপেক্ষা ছোট সংখ্যা গুলিকে ঋণাত্মক পূর্ণসংখ্যা ( Negative Integer ) বলে ।
মূলদ সংখ্যা ( Rational Number ) : যে সংখ্যাকে দুটি পূর্ণ সংখ্যার ভগ্নাংশরূপে প্রকাশ করা যায় , তাকে মূলদ সংখ্যা বলে। যদি p এবং q দুটি অখণ্ড সংখ্যা হয় , এমন p এবং q সংখ্যা দুটি পরস্পর মৌলিক অর্থাৎ 1 ছাড়া কোনো সাধারণ উৎপাদক নেই এবং q≠0 তবে pq আকারের সংখ্যাকে মূলদ সংখ্যা বলে । মূলদ সংখ্যার দলকে সাধারণ ভাবে Q দ্বারা প্রকাশ করা হয়। অতএব
Q = { pq ; p এবং q পূর্ণসংখ্যা q≠0 }
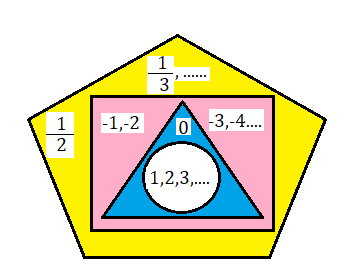
মনে রাখতে হবে পূর্ণসংখ্যা অর্থাৎ শূন্য ও সমস্ত স্বাভাবিক সংখ্যার মত মূলদ সংখ্যা গুলিকেও সংখ্যা অক্ষ বা সংখ্যা রেখার উপরে স্থাপন করা যায় । উপরের চিত্র থেকে বোঝা যাচ্ছে সকল পূর্ণসংখ্যা মূলদ সংখ্যা ।
মূলদ সংখ্যার সংখ্যা অক্ষ হল
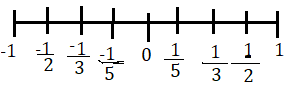
সংখ্যা অক্ষ থেকে দেখা যাচ্ছে যে 0 ও 1 কিংবা 0 ও -1 এর মধ্যে অসংখ্য মূলদ সংখ্যা আছে ।
সমতুল্য মূলদ সংখ্যা ( Equivalent rational number ) বা সমতুল্য ভগ্নাংশ ( Equivalent fraction )
মনে করি 610,1220,915,..... ভগ্নাংশ গুলি সবাই 35 এর সঙ্গে সমান বা এর সমতুল্য , তাই এদেরকে সমতুল্য মূলদ সংখ্যা বা সমতুল্য ভগ্নাংশ বলে ।
অমূলদ সংখ্যা ( Irrational number )
আমরা দেখেছি যে সকল সংখ্যাকে pq আকারে প্রকাশ করা যায় যেখানে p এবং q পূর্ণসংখ্যা এবং q≠0 তাদের সকলকে মূলদ সংখ্যা বলে এবং এই সংখ্যা গুলিকে আমরা সংখ্যা অক্ষে স্থাপন করেছি । কিন্তু বাকি সংখ্যা অর্থাৎ যে সমস্ত সংখ্যাকে pq আকারে প্রকাশ করা যায়না যেখানে p এবং q পূর্ণসংখ্যা এবং q≠0 তাদের কে কী বলব ?
যে সকল সংখ্যাকে pq আকারে প্রকাশ করা যায়না যেখানে p এবং q পূর্ণসংখ্যা এবং q≠0 তাদেরকে অমূলদ সংখ্যা ( Irrational number ) বলা হয় ।
যেমন : √2,√3,3√4,√5,.......... ইত্যাদি ।
গ্রিসের দার্শনিক ও গণিতজ্ঞ পিথাগোরাসের অনুগামীরা প্রায় 400 BC তে প্রথম অমূলদ সংখ্যার ধারণা দেন । তাঁরা সংখ্যা রেখার মূলদ সংখ্যা ছাড়াও আরও সংখ্যার অস্তিত্ব অনুভব করেন । পরবর্তীকালের বিশিষ্ট গণিতজ্ঞগণ বিভিন্ন অমূলদ সংখ্যার ধারণা দিয়েছেন এবং অমূলদ সংখ্যার সন্ধান এখনো চলেছে ।
প্রমাণ করে দেখা যাক √2 একটি অমূলদ সংখ্যা
প্রমাণ : মনে করি √2 একটি মূলদ সংখ্যা অর্থাৎ √2 কে pq আকারে প্রকাশ করা যায়। যেখানে p ও q দুটি অখন্ড সংখ্যা এবং পরস্পর মৌলিক এবং q≠0.
অতএব আমরা বলতে পারি √2=pq⇒2=p2q2
অতএব p2=2q2
এখন ডানপক্ষ যেহেতু 2 এর গুণিতক তাহলে বামপক্ষ অবশ্যই 2 এর গুণিতক হবে। অতএব p2 বা p অবশ্যই একটি জোড় সংখ্যা ।
ধরি p = 2r
তাহলে
p2=2q2⇒(2r)2=2q2⇒4r2=2q2⇒q2=2r2
এখন দেখা যাচ্ছে q একটি জোড় সংখ্যা। অর্থাৎ এর থেকে বোঝা যাচ্ছে p এবং q উভয়েই জোড়সংখ্যা। তাদের মধ্যে একটি সাধারণ উৎপাদক হল 2 . কিন্তু আমরা প্রথমেই ধরে ছিলাম p এবং q পরস্পর মৌলিক । সুতরাং √2 একটি মূলদ সংখ্যা এই ধারণাটি ভুল । অতএব প্রমাণিত √2 একটি অমূলদ সংখ্যা ।
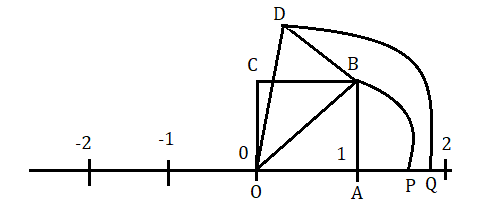
অমূলদ সংখ্যা কেও সংখ্যারেখায় স্থাপন করা যায়। যেমন √2,√3,√5 কে কিভাবে সংখ্যারেখায় স্থাপন করা হয় তা দেখানো হল ।
√2 সংখ্যারেখায় স্থাপন
মনে করি O বিন্দুটি হল সংখ্যারেখার মূলবিন্দু। এখন OA = 1 একক ধরে সংখ্যা অক্ষের উপরে OABC একটি বর্গক্ষেত্র অঙ্কন করা হল ।
অতএব AB = 1 একক . এখন কর্ণ OB এর দৈর্ঘ্য হল 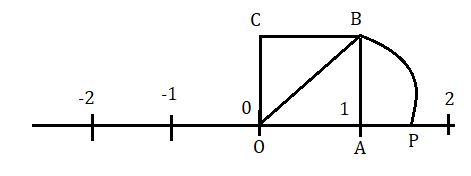
√OA2+BA2 একক
=√1+1 একক
=√2 একক
এবার O বিন্দুতে কাঁটা কম্পাসের কাঁটা বসিয়ে OB ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ অঙ্কন করা হল যা সংখ্যা অক্ষকে P বিন্দুতে ছেদ করেছে। OP = √2 একক ।
√3 সংখ্যারেখায় স্থাপন
এখন OB রেখার উপরে BD লম্ব টানা হল OD যুক্ত করা হল .
পিথাগোরাসের উপপাদ্য অনুযায়ী
 OD=√OB2+BD2=√(√2)2+1=√2+1=√3
OD=√OB2+BD2=√(√2)2+1=√2+1=√3
অতএব O বিন্দু থেকে OD এর সমান ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ অঙ্কন করা হল যা সংখ্যারেখাকে Q বিন্দুতে ছেদ করেছে। অতএব OQ = √3 একক ।
একই ভাবে √5 কে আমরা সংখ্যারেখায় স্থাপন করতে পারি ।
বিশেষ দ্রষ্টব্যঃ
- যে সমস্ত সংখ্যাকে pq [ p , q দুটি অখণ্ড সংখ্যা পরস্পর মৌলিক এবং q≠0 ] এরকম ভগ্নাংশের আকারে প্রকাশ করা যায় না , সেগুলিকে অমূলদ সংখ্যা বলে ।
- প্রতিটি মূলদ সংখ্যাই একটি ভগ্নাংশ , কিন্তু ভগ্নাংশ মাত্রই মূলদ সংখ্যা নয় । যেমন 14,25,38 ইত্যাদি সংখ্যাগুলি মূলদ । তাছাড়া অখণ্ড সংখ্যাগুলিও মূলদ যেমন 2 , 3 ইত্যাদিকে 21,31 আকারে প্রকাশ করা যায় । কিন্তু √2,3√3 কে ভগ্নাংশের আকারে প্রকাশ করা গেলেও এরা মূলদ সংখ্যা নয় ।
- সংখ্যারেখার উপরে মূলদ বিন্দুগুলি নিবিড় ভাবে অবস্থান করে অর্থাৎ সংখ্যারেখার উপরে যে কোনো দুটি মূলদ বিন্দুর মধ্যবর্তী স্থানে অসংখ্য মূলদ বিন্দু অবস্থিত থাকে ।
- মজার কথা হল সংখ্যারেখার উপরে মূলদসংখ্যার চেয়ে অমূলদ সংখ্যার পরিমান অনেক বেশি ।
- দুটি মূলদ সংখ্যার যোগফল বা বিয়োগফল অবশ্যই একটি মূলদ সংখ্যা ।
- একটি মূলদ সংখ্যা কখনোই একটি অমূলদ সংখ্যার সমান হতে পারেনা ।
- দুটি মূলদ সংখ্যার গুণফল একটি মূলদ সংখ্যা ।
- দুটি অমূলদ সংখ্যার যোগফল কখনো অমূলদ বা কখনো মূলদ হতে পারে , যেমন (2+√3) এবং (2−√3) এর যোগফল 4 একটি মূলদ সংখ্যা । কিন্তু (√3+2) এবং (√3−2) এর যোগফল 2√3 একটি অমূলদ সংখ্যা ।
- একটি মূলদ এবং একটি অমূলদ সংখ্যার যোগফল সর্বদা একটি অমূলদ সংখ্যা হবে ।
- দুটি অমূলদ সংখ্যার গুণফল কখনো অমূলদ বা কখনো মূলদ হতে পারে ।
বাস্তব সংখ্যা ( Real Number ) : মূলদ সংখ্যার সাথে অমূলদ সংখ্যা গুলিকে একত্রিত করে যে সকল সংখ্যা পাওয়া যায় , তাদের বাস্তব সংখ্যা বলে। বাস্তব সংখ্যার দলকে R চিহ্ন দ্বারা প্রকাশ করা হয় ।
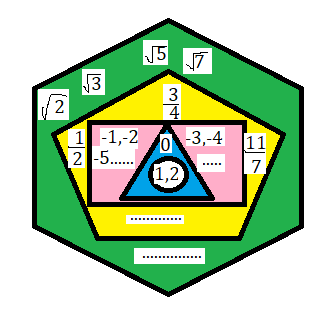
বাস্তব সংখ্যা অত্যন্ত নিবিড় । এদের মধ্যে কোনো ফাঁক থাকে না । বাস্তব অক্ষের উপরে অবস্থিত প্রতিটি বিন্দু বাস্তব সংখ্যাকে প্রকাশ করে । এগুলি প্রতিটি বাস্তব বিন্দু । মূলদ সংখ্যাও নিবিড় কিন্তু এরা যথেষ্ট নিবিড় নয় । দুটি মূলদ সংখ্যার মধ্যে ফাঁক বর্তমান। সংখ্যা অক্ষের উপরে দুটি মূলদ বিন্দুর মাঝে অনেক বিন্দু থেকে যারা মূলদ বিন্দু নয় । ওই বিন্দুগুলিকে অমূলদ বিন্দু বলে ।
যে কোনো বাস্তব সংখ্যার সাংখ্যমান হল তার পরম মান । বাস্তব সংখ্যার সাংখ্যমান কখনো ঋণাত্মক হয় না । যদি কোনো বাস্তব সংখ্যা a হয় তবে তার পরম মান ।a। চিহ্ন দ্বারা প্রকাশ করা হয় ।
বাস্তব সংখ্যার ধর্ম
- দুটি বাস্তব সংখ্যার যোগফল , বিয়োগফল , ভাগফল ও গুণফল সর্বদা একটি বাস্তব সংখ্যা হবে ।
- বাস্তব সংখ্যার গণিতের সাধারণ সূত্র বিনিময় , সংযোগ , বিচ্ছেদ সূত্র সিদ্ধ করে ।
- বাস্তব সংখ্যা ত্রিভাগ নিয়ম ( trichotomy law ) মেনে চলে। যেমন x , y দুটি বাস্তব সংখ্যা হলে x > y , x = y , x < y .
- বাস্তব সংখ্যা ক্রম নিয়ম ( order law ) মেনে চলে। x , y , z তিনটি বাস্তব সংখ্যা এবং x≥y , y > z হলে x > z হব ।
- বাস্তব সংখ্যা অত্যন্ত নিবিড় । দুটি বাস্তব সংখ্যার মধ্যে অসংখ্য বাস্তব সংখ্যা থাকে । সংখ্যা অক্ষের উপরে অবস্থিত যেকোনো দুটি বাস্তব বিন্দুর মধ্যে বাস্তব সংখ্যা প্রকাশ করেনা এমন কোনো বিন্দু থাকতে পারেনা ।
- বাস্তব সংখ্যা দ্বারা যেকোনো দৈর্ঘ্য পরিমাপ করা যায় ।
- গণিতের সমস্ত সংখ্যা বাস্তব সেটের অন্তর্গত ।
- বাস্তব সংখ্যাকে দশমীকে প্রকাশ করলে তা সসীম , অসীম , আবৃত্ত হতে পারে। আবার অসীম অপৌনঃপুনিক হতে পারে। সসীম , অসীম , আবৃত্ত হলে বাস্তব সংখ্যা টি মূলদ হবে । অসীম ও অপৌনঃপুনিক হলে অমূলদ হবে ।
বাস্তব সংখ্যার গণিতের সাধারণ সূত্র বিনিময় , সংযোগ , বিচ্ছেদ সূত্র সিদ্ধ করে
x , y এবং z তিনটি বাস্তব সংখ্যা হলে
- x + y = y + x ( যোগের বিনিময় সূত্র )
- x×y=y×x ( গুণের বিনিময় সূত্র )
- ( x + y ) + z = x + ( y + z ) ( যোগের সংযোগ সূত্র )
- (x×y)×z=x×(y×z) ( গুণের সংযোগ সূত্র )
- (x+y)×z=(x×z)+(y×z) এবং x×(y+z)=(x×y)+(x×z) ( বিচ্ছেদ সূত্র )
53 বাস্তব সংখ্যাকে দশমীকে প্রকাশ করে পাই
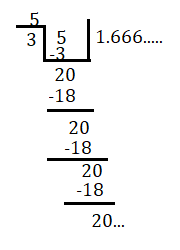
53=1.666..............=1.˙6 ভাগশেষ 2 , 2 , 2 ...., ভাজক 3 .
দেখা যাচ্ছে ভাগশেষ কখনো 0 হচ্ছেনা। অর্থাৎ দশমিকে বিস্তার করায় আবৃত্ত দশমিক পাচ্ছি।
311 মূলদ সংখ্যাকে দশমিকে প্রকাশ করে পাই
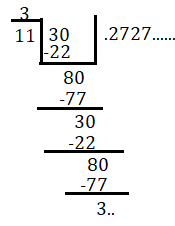
311 কে দশমিকে প্রকাশ করে পাই 311=0.˙2˙7 এটি একটি আবৃত্ত দশমিক সংখ্যা।
58 মূলদ সংখ্যাকে দশমিকের আকারে প্রকাশ করো।
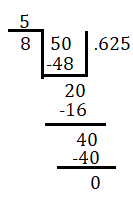
58 কে এর দশমিকের আকারে প্রকাশ করলে হয় 58=0.625
বিশেষ দ্রষ্টব্যঃ
যে সমস্ত বাস্তব সংখ্যার হরের মৌলিক উৎপাদকে কেবলমাত্র 2 এবং 5 থাকে সেই সমস্ত সংখ্যার দশমিক আকারে প্রকাশে ভাগশেষ সর্বদা শূন্য হয়ে যায়।
pq আকারের কোনো মূলদ সংখ্যার হর অর্থাৎ q অংশে 2 কিংবা 5 ছাড়া কোনো উৎপাদক না থাকলে সেই মূলদ সংখ্যা একটি সসীম ( Termination decimal ) পাওয়া যায়।
আবার pq আকারের কোনো মূলদ সংখ্যার হর অর্থাৎ q অংশে 2 অথবা 5 অন্য একটি মৌলিক সংখ্যা উৎপাদক হিসাবে থাকলে সেই মূলদ সংখ্যা একটি অসীম দশমিক সংখ্যা ( non termination decimal ) পাওয়া যায়।
5.875,2.˙6,0.˙4˙5 ,1.˙28571˙4 এবং 0.1˙3˙6 এই সংখ্যা গুলিকে ভগ্নাংশে প্রকাশ করো।
5.875=58751000=478
2.˙6=2+.˙6=2+69=2+23=223=83
0.˙4˙5=4599=511
1.˙28571˙4=1+.˙28571˙4=1+285714999999=1+2×1428577×142857=1+27=97
0.1˙3˙6=136−1990=135990=322
অমূলদ সংখ্যাকে দশমিকে প্রকাশ করলে কি পাওয়া যায়
অমূলদ সংখ্যাকে দশমিকে প্রকাশ করলে অসীম অনাবৃত্ত দশমিক সংখ্যা পাবো ( non termination and non recurring ) এবং যে দশমিকের বিস্তার অসীম অনাবৃত্ত দশমিক সংখ্যা , সেই সংখ্যা অমূলদ সংখ্যা। যেমন 0.4504500450004500045......... এটি একটি অমূলদ সংখ্যা কারণ এটি অসীম ও অনাবৃত।
√2 কে দশমিকে বিস্তার করলে পাই
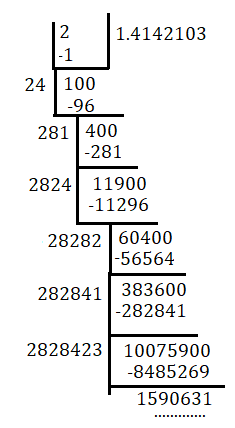
সংখ্যারেখায় 5.672 বিন্দুর স্থাপন

সংখ্যারেখা থেকে পরিষ্কার বোঝা যাচ্ছে যে 5.672 বিন্দুটি 5 এবং 6 এর মধ্যবর্তী কোনো স্থানে থাকবে।
এখন 5 এবং 6 এর মধ্যবর্তী জায়গাটিকে সমান দশ ভাগ করে পাই

এই চিত্র থেকে বোঝা যাচ্ছে 5.672 বিন্দুটি 5.6 এবং 5.7 এই দুটি বিন্দুর মধ্যে থাকবে। এখন 5.6 এবং 5.7 এই দুটি বিন্দুর মধ্যবর্তী স্থানকে আবার সমান দশ ভাগ করে পাই।
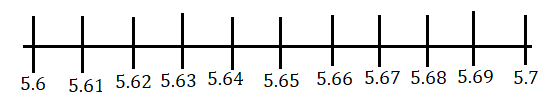
এই চিত্র থেকে বোঝা যাচ্ছে 5.672 বিন্দুটি সংখ্যারেখায় 5.67 এবং 5.68 এর মধ্যবর্তী স্থানে থাকবে। আবার 5.67 এবং 5.68 এর মধ্যবর্তী স্থান কে সমান দশ ভাগ করে পাই।
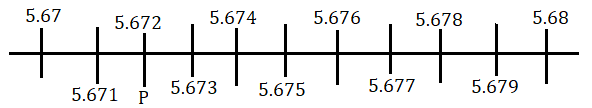
দেখা যাচ্ছে P বিন্দুটি হল 5.672 বিন্দুর অবস্থান। সংখ্যারেখায় 5.672 বিন্দুটি স্থাপন করে আমরা P বিন্দু পেলাম।
5.3˙7 বিন্দুটিকে সংখ্যারেখায় স্থাপন

সংখ্যারেখা থেকে পরিষ্কার বোঝা যাচ্ছে 5.3˙7 বিন্দুটি 5 এবং 6 এর মধ্যবর্তী কোনো স্থানে থাকবে। এখন 5 এবং 6 এর মধ্যবর্তী অংশ কে সমান দশ ভাগে ভাগ করে পাই।

চিত্র থেকে বোঝা যাচ্ছে 5.3˙7 বিন্দুটি 5.3 এবং 5.4 এর মধ্যবর্তী কোনো স্থানে থাকবে। এখন আরো নিখুঁত অবস্থান বোঝার জন্য 5.3 এবং 5.4 এর মধ্যবর্তী অংশ কে সমান দশ ভাগ করে পাই।
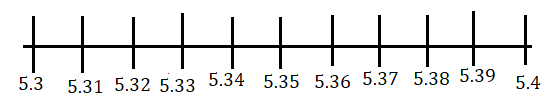
দেখা যাচ্ছে 5.3˙7 বিন্দুটি 5.37 এবং 5.38 এর মধ্যবর্তী কোনো স্থানে থাকবে। এখন 5.37 এবং 5.38 এর মধ্যবর্তী স্থানটিকে সমান দশ ভাগ করে পাই
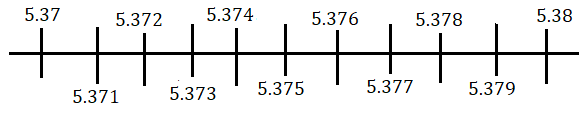
দেখা যাচ্ছে 5.3˙7 বিন্দুটি 5.377 এবং 5.378 এর মধ্যবর্তী কোনো স্থানে থাকবে। এখন আরো নিখুঁত অবস্থান বোঝার জন্য 5.377 এবং 5.378 এর মধ্যবর্তী অবস্থানকে আবার দশ ভাগে ভাগ করলাম।
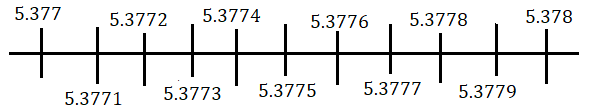
5.3˙7 বিন্দুটি 5.3777 এবং 5.3778 এর মধ্যে অবস্থান করছে। যেহেতু 5.3˙7 একটি আবৃত্ত দশমিক তাই এই ভাবেই চলতে থাকবে ।
*****
- 37584 views