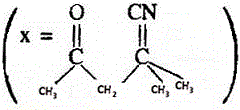
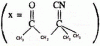Q. 1 – Q. 45 carry one mark each, for which only one option is correct. Any wrong answer will be lead to deduction of 1/3 mark.
1. একটি গ্যাসের অবস্থার সমীকরণ হল (P+aV3)(V−b2)=cT, যেখানে P, V, T যথাক্রমে চাপ, আয়তন ও উষ্ণতা এবং a, b, c ধ্রুবক । তা হলে a এবং b -এর মাত্রা হল যথাক্রমে
(A) ML8T−2 এবং L3/2 (B) ML5T−2 এবং L3 (C) ML5T−2 এবং L6 (D) ML6T−2 এবং L3/2
2. C0 ধারকত্ব বিশিষ্ট একটি ধারককে V0 বিভব প্রভেদে আহিত করে অন্য একটি C ধারকত্ব বিশিষ্ট ধারককের সঙ্গে চিত্রের বর্তনী অনুযায়ী সংযুক্ত করা হল । বর্তনীর সুইচ S -টি বন্ধ করলে উভয় ধারকের বিভব প্রভেদ হয় V । তাহলে C -এর মান হল

(A) C0(V0−V)V0 (B) C0(V−V0)V0 (C) C0(V+V0)V (D) C0(V0−V)V
3. 100°সেঃ উষ্ণতায় গ্যাসের অণুর গড়-বর্গ বেগের বর্গমূল (r.m.s. বেগ ) হল v । যে উষ্ণতায় গড়-বর্গ বেগের বর্গমূল √3v হবে তা হল
(A) 546°C (B) 646°C (C) 746°C (D) 846°C
4. নীচের চিত্রের ন্যায় একটি +2C আধানকে মূল বিন্দু O -তে স্থাপন করা হয়েছে । একটি +5C আধানকে x -অক্ষের ওপর অবস্থিত একটি বিন্দু A থেকে y -অক্ষের ওপর অবস্থিত আরেকটি বিন্দু B -তে নিয়ে যেতে কৃত কার্য হবে
(দেওয়া আছে 14πϵ0=9×109m/F)
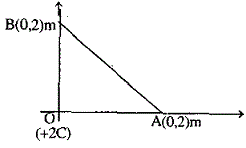
(A) 45×109 J (B) 90×109 J (C) Zero (D) −45×109 J
5. ঘর্ষণহীন পিস্টন যুক্ত একটি চোঙের মধ্যে 400 kPa চাপে একটি গ্যাস আবদ্ধ আছে । বাইরে থেকে তাপ সরবরাহ করে প্রায় স্থির (quasi-static) পদ্ধতিতে চাপ অপরিবর্তিত রেখে গ্যাসের উষ্ণতা বৃদ্ধি করা হল । পিস্টনটি ধীরে ধীরে 10 cm উচ্চতা উঠে গেল । পিস্টনের প্রস্থচ্ছেদের ক্ষেত্রফল 0.3 m² হলে গ্যাস কর্তৃক কৃত কার্য হল
(A) 6 kJ (B) 12 kJ (C) 7.5 kJ (D) 24 kJ
6. d ব্যাস ও l দৈর্ঘ্য বিশিষ্ট একটি তামার তারের দুই প্রান্তের মধ্যে E তড়িচ্চালক বল প্রয়োগ করলে তারের মধ্যে ইলেকট্রনের প্রবাহবেগ হয় vd । এখন তারের দৈর্ঘ্য পরিবর্তিত করে 2l করলে তারের মধ্যে ইলেকট্রনের নতুন প্রবাহবেগ হবে
(A) vd (B) 2vd (C) vd/2 (D) vd/4
7. একটি NOR গেট এবং একটি NAND গেটকে চিত্রানুযায়ী যুক্ত করা হল । এই ব্যবস্থাটিতে দুটি ভিন্ন ক্ষেত্রে কিছু ইনপুট দেওয়া হল । প্রথম ক্ষেত্রে গেটগুলির ইনপুট A = 0, B = 0, C = 0 এবং দ্বিতীয় ক্ষেত্রে গেটগুলির ইনপুট A = 1, B = 0, C = 1 । প্রথম ও দ্বিতীয় ক্ষেত্রের আউটপুট D হবে যথাক্রমে
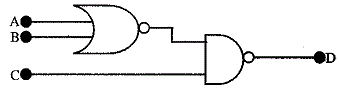
(A) 0 এবং 0 (B) 0 এবং 1 (C) 1 এবং 0 (D) 1 এবং 1
8. একটি দন্ড চুম্বকের চৌম্বক ভ্রামক 200 A.m² । এই চুম্বককে 0.30 NA-1m-1 চৌম্বক ক্ষেত্রে ঝুলিয়ে রাখা হল । চুম্বকের সাম্যস্থান থেকে 30° ঘোরাতে যে টর্কের (দ্বন্দ্বের) প্রয়োজন হয় তা হল
(A) 30 N m (B) 30√3 N m (C) 60 N m (D) 60√3 N m
9. যথাক্রমে r ও 2r ব্যাসার্ধের দুটি সাবান বুদবুদকে একটি কৈশিক নলের সাহায্যে চিত্রের ন্যায় সংযুক্ত করা হল এবং কৈশিক নলের ভালভ টি খুলে দেওয়া হল । এর ফলে :
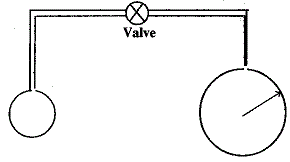
(A) বুদবুদগুলির ব্যাসার্ধ অপরিবর্তিত থাকবে
(B) বুদবুদগুলির ব্যাসার্ধ সমান হয়ে যাবে
(C) ছোটো বুদবুদটির ব্যাসার্ধ বৃদ্ধি পাবে এবং বড়ো বুদবুদটির ব্যাসার্ধ হ্রাস পাবে
(D) ছোটো বুদবুদটির ব্যাসার্ধ হ্রাস পাবে এবং বড়ো বুদবুদটির ব্যাসার্ধ বৃদ্ধি পাবে
10. নির্দিষ্ট ভরের একটি এক পরমাণুক আদর্শ গ্যাসকে চাপ স্থির রেখে উত্তপ্ত করা হল । এই পদ্ধতিতে সরবরাহকৃত তাপশক্তির যে ভগ্নাংশ গ্যাসের অভ্যন্তরীণ শক্তি বৃদ্ধির জন্য ব্যবহৃত হয়, তা হল
(A) 3/8 (B) 3/5 (C) 3/4 (D) 2/5
11. সোজা রাস্তায় চলমান একটি গাড়ির কোনো এক মুহুর্তের গতিবেগ হল 36 kmh-1 । সমত্বরণে চলমান এই শক্তির গতিবেগ 10 s পরে ঠিক দ্বিগুণ হয় । গাড়ির চাকার ব্যাসার্ধ 25 cm । এই 10 s সময়ে একটি চাকার যতগুলি পূর্ণ আবর্তন ঘটেছে তার মান নীচের কোন সংখ্যাটির সর্বাপেক্ষা কাছাকাছি হবে ?
(A) 84 (B) 95 (C) 126 (D) 135
12. দুটি প্রিজম P1 ও P2 কে এমনভাবে যুক্ত করা হল, যাতে চ্যুতিহীন বিচ্ছুরণ ঘটে । P1 ও P2 প্রিজমের প্রতিসারক কোণগুলি যথাক্রমে 4° ও 3° হলে P1 -এর উপাদানের প্রতিসরাঙ্ক 1.54 হলে, P2 -এর উপাদানের প্রতিসরাঙ্ক হবে
(A) 1.48 (B) 1.58 (C) 1.62 (D) 1.72
13. হাইড্রোজেন পরমাণুর আয়নন শক্তি হল 13.6 eV । হাইড্রোজেনের n = 2 কক্ষপথের ইলেকট্রনের স্থিতিশক্তি হল হল
(A) +3.4 eV (B) -3.4 eV (C) +6.8 eV (D) -6.8 eV
14. অনুভূমিক নলের ভিতর দিয়ে জলের ধারারেখ প্রবাহ হচ্ছে । নলের কোন বিন্দুতে চাপ p ও প্রবাহ বেগ v । অন্য একটি বিন্দুতে চাপ p/2 হলে সেখানে জলের প্রবাহ বেগ হবে [জলের ঘনত্ব = ρ]
(A) √v2+pρ (B) √v2−pρ (C) √v2+2pρ (D) √v2−2pρ
15. নীচের তড়িৎ বর্তনীতে 4Ω রোধের মধ্যে দিয়ে তড়িৎ প্রবাহমাত্রা হল
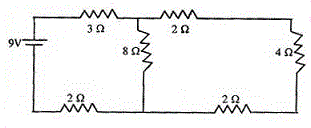
(A) 1 A (B) 0.5 A (C) 0.25 A (D) 0.1 A
16. প্রথমে r প্রস্থচ্ছেদের ব্যাসার্ধ ও L প্রাথমিক দৈর্ঘ্য বিশিষ্ট একটি তারের l পরিমাণ দৈর্ঘ্য বৃদ্ধি ঘটানো হল । দ্বিতীয় ক্ষেত্রে, একই পদার্থের তৈরি 2r প্রস্থচ্ছেদের ব্যাসার্ধ ও 2L প্রাথমিক দৈর্ঘ্য বিশিষ্ট আরেকটি তারের 2l পরিমাণ দৈর্ঘ্য বৃদ্ধি ঘটানো হল । প্রথম ও দ্বিতীয় ক্ষেত্রে দুটি তারে প্রতি একক আয়তনে সঞ্চিত স্থিতি শক্তির অনুপাত হবে
(A) 1 : 4 (B) 1 : 2 (C) 2 : 1 (D) 1 : 1
17. 0.5 m দৈর্ঘ্যের একটি ঋজু পরিবাহীর ভিতর দিয়ে ধনাত্মক x অক্ষ বরাবর 1 A তড়িৎ প্রবাহমাত্রা যাচ্ছে । এই পরিবাহীটিকে একটি চৌম্বকক্ষেত্র →B=(2ˆi+4ˆj)T -র মধ্যে রাখা হলে পরিবাহী তারের ওপর যে বল প্রযুক্ত হবে তার মান ও দিক যথাক্রমে
(A) √18 N, ধনাত্মক z -অক্ষ বরাবর
(B) √20 N, ধনাত্মক x -অক্ষ বরাবর
(C) 2N, ধনাত্মক z -অক্ষ বরাবর
(D) 4N, ধনাত্মক y -অক্ষ বরাবর
18. একই পদার্থের তৈরি দুটি গোলকের ব্যাসার্ধ যথাক্রমে R এবং 3R । তাদের σ ঘনত্বের একটি তরলের মধ্য দিয়ে নীচের দিকে পড়তে দেওয়া হল । তাদের প্রান্তীয় গতিবেগের অনুপাত হবে
(A) 1 : 3 (B) 1 : 6 (C) 1 : 9 (D) 1 : 1
19. xy -তলে দুইটি সুসংবদ্ধ আলোকের উত্সবিন্দু S1 এবং S2 যথাক্রমে (0, 0) এবং (0, 3λ) বিন্দুতে অবস্থিত । বিন্দু দুটি থেকে নির্গত আলোকের তরঙ্গদৈর্ঘ্য λ, নিম্নলিখিত কোনো বিন্দুতে (যাদের স্থানাঙ্ক দেওয়া আছে) আলোকের ব্যতিচারের তীব্রতা সর্বোচ্চ হবে ?
(A) (3λ, 0) (B) (4λ, 0) (C) (5λ/4, 0) (D) (2λ/3, 0)
20. আলফা কণা (4He) -র ভর 4.00300 amu । একটি প্রোটনের ভর 1.00783 amu এবং একটি নিউট্রনের ভর 1.00867 amu । প্রদত্ত তথ্য থেকে আলফা কণার বন্ধন শক্তি গণনা করা হলে তা নীচের যে মানের সর্বাপেক্ষা নিকটবর্তী হবে, তা হল
(A) 27.9 MeV (B) 22.3 MeV (C) 35.0 MeV (D) 20.4 MeV
21. প্রতিটি m ভর বিশিষ্ট চারটি বস্তুকণা একটি নগণ্য ভরের তারের তৈরি আয়তকার কাঠামোর চারটি কোণায় স্থাপন করা হল । আয়তক্ষেত্রটির বাহুদ্বয়ের দৈর্ঘ্য a এবং b (a > b) । এবার b দৈর্ঘ্যের একটি বাহুকে অক্ষ করে তার চারদিকে সমগ্র ব্যবস্থাটিকে ঘোরানো হল । এই ঘূর্ণন অক্ষের সাপেক্ষে সামগ্রিক ব্যবস্থাটির জড়তা ভ্রামক হবে
(A) 2ma² (B) 4ma² (C) 2m(a² + b²) (D) 2m(a² - b²)
22. চিত্রে দেখানো বৈদ্যুতিক নেটওয়ার্ক বা জালিকার ক্ষেত্রে a এবং b বিন্দুর মধ্যে তুল্য রোধ হল
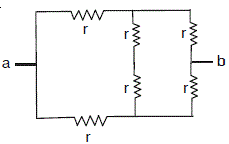
(A) 6r (B) 4r (C) 2r (D) r
23. 200 eV গতিশক্তির একটি ইলেকট্রনের (ভর = 1 x 10-30 kg, আধান = 1.6 x 10-19 C) দ্য ব্রয় তরঙ্গ দৈর্ঘ্য হল (প্ল্যাঙ্কের ধ্রুবক = 6.6 x 10-34 Js)
(A) 9.60 x 10-11 m (B) 8.25 x 10-11 m (C) 6.25 x 10-11 m (D) 5.00 x 10-11 m
24. একটি উত্তল লেন্সের থেকে 16 cm দূরত্বে একটি বস্তুকে রাখলে তার m গুণ (m > 1) বিবর্ধিত প্রতিবিম্ব তৈরি হয় । বস্তুটিকে লেন্সের দিকে 8 cm সরালে আবার ওই m বিবর্ধন বিশিষ্ট প্রতিবিম্ব পাওয়া যায় । লেন্সটির ফোকাস দূরত্বের সাংখ্যমান (numerical value) হল
(A) 12 cm (B) 14 cm (C) 18 cm (D) 20 cm
25. T অর্ধায়ু বিশিষ্ট একটি তেজস্ক্রিয় পদার্থের t = 0 সময়ে পরমাণুর সংখ্যা N0 । পদার্থটির পরমাণুর সংখ্যা N0/2 থেকে N0/10 কমতে যে সময় লাগবে, তা হল
(A) 52T (B) Tln5 (C) Tln(52) (D) Tln5ln2
26. 500 Hz কম্পাঙ্ক বিশিষ্ট একটি শব্দতরঙ্গ 300 ms-1 বেগে ধনাত্মক x অক্ষ বরাবর অগ্রসর হচ্ছে । x1 এবং x2 বিন্দু দুটিতে এই তরঙ্গের দশার পার্থক্য 60° । তা হলে এই বিন্দু দুটির নূন্যতম দূরত্ব হবে
(A) 1 mm (B) 1 cm (C) 10 cm (D) 1 m
27. স্থির অবস্থায় রাখা M ভরের একটি বস্তু m ও (M - m) ভরের দুটি অংশে বিভক্ত করা হল । এই দুটি বস্তু খন্ডের মধ্যে দূরত্ব r । বস্তুখন্ড দুটির ভরের অনুপাত [m : (M - m)] কত হলে তাদের মধ্যে মহাকর্ষজনিত আকর্ষণ বল সর্বোচ্চ হবে ?
(A) 1 : 1 (B) 1 : 2 (C) 1 : 3 (D) 1 : 4
28. 5M ভরের একটি গোলার ওপর কোনো বহিঃস্থ বল ক্রিয়া করছে না এবং তা প্রাথমিক ভাবে স্থির অবস্থায় আছে । গোলাটির বিস্ফোরণ হল এবং সেটি M, 2M এবং 2M ভরের তিনটি অংশে বিভক্ত হয়ে গেল । প্রথম অংশ দুটি যথাক্রমে 2V এবং V বেগে বিপরীত দিকে চলে গেলে তৃতীয় অংশটি
(A) V বেগে প্রথম দুটির গতি অভিমুখে অভিলম্ব বরাবর যাবে
(B) 2V বেগে প্রথম খন্ডটির দিক বরাবর যাবে
(C) স্থির অবস্থায় থাকবে
(D) V বেগে দ্বিতীয় খন্ডটির দিক বরাবর যাবে
29. m ভরের একটি বুলেট v বেগে ধাবিত হয়ে স্থিরাবস্থায় থাকা M ভরের একটি বস্তুকে আঘাত করল এবং তার মধ্যে প্রবিষ্ট হয়ে গেল । এই দুটি ভরের বস্তু সমষ্টিটি মুক্তভাবে বিচরণ করতে পারে এবং তাদের ওপর কোনো বাহ্যিক বল ক্রিয়া করছে না । এই প্রক্রিয়াটিতে যে তাপ সৃষ্টি হবে তার পরিমাণ হল
(A) Zero (B) mv22 (C) Mmv22(M−m) (D) mMv22(M+m)
30. একটি বস্তুকণা X -অক্ষ বরাবর যাচ্ছে এবং কোনো সময় তার সরণ হল x(t) = 2t³ - 3t² + 4t (SI এককে) । তাহলে কণাটির ত্বরণ যখন শূন্য হবে তখন তার বেগ হবে
(A) 2.5 ms-1 (B) 3.5 ms-1 (C) 4.5 ms-1 (D) 8.5 ms-1
31. একটি গ্রহ সূর্যকে উপবৃত্তাকার কক্ষপথে প্রদক্ষিণ করছে এবং সূর্য ওই কক্ষপথের একটি ফোকাসে রয়েছে । গ্রহটির এই আবর্তনের সময় সংশ্লিষ্ট যে ভৌত রাশিটি ধ্রুবক হিসাবে থাকবে তা হল
(A) গতিবেগ (B) অভিকেন্দ্র বল (C) রৈখিক গতিবেগ (D) কৌণিক গতিবেগ
32. একটি বন্ধ নলে শব্দতরঙ্গের মূল সুর ও একটি খোলা নলের দ্বিতীয় সমমেলের কম্পাঙ্ক সমান । নল দুটির দৈর্ঘ্যের অনুপাত হবে
(A) 1 : 2 (B) 1 : 4 (C) 1 : 8 (D) 1 : 16
33. M ভর ও q আধান বিশিষ্ট একটি কণাকে কোনো সুষম তড়িৎ ক্ষেত্রে (মান E) ছেড়ে দেওয়া হল । t সময় পরে কণাটি S দূরত্ব অতিক্রম করে এবং T গতিশক্তি অর্জন করে । সেক্ষেত্রে T/S অনুপাত
(A) সময় t -এর সঙ্গে অপরিবর্তিত থাকবে
(B) কণার ভর M -এর সাথে সমানুপাতে পরিবর্তিত হবে
(C) আধানের মানের ওপর নির্ভর করবে না
(D) তড়িৎ ক্ষেত্রের মানের ওপর নির্ভর করবে না
34. একটি বর্তনীতে পরিবর্তী প্রবাহ I=20sin(100πt+0.05π) A হলে প্রবাহমাত্রার গড় বেগের বর্গমূল বা r.m.s মান ও কম্পাঙ্ক যথাক্রমে
(A) 10 A এবং 100 Hz (B) 10 A এবং 50 Hz (C) 10√2 A এবং 50 Hz (D) 10√2 A এবং 100 Hz
35. নিম্ন তাপমাত্রায় কোনো একটি পদার্থের আপেক্ষিক তাপ c তাপমাত্রার ওপর c = DT³ সম্পর্ক অনুযায়ী নির্ভর করে, যেখানে D একটি ধ্রুবক এবং T চরম তাপমাত্রা । এই কঠিন পদার্থের m kg ভরকে 20 K থেকে 30 K তাপমাত্রায় নিয়ে যেতে যে পরিমাণ তাপের প্রয়োজন হবে, শক্তির এককে তার পরিমাণ হল
(A) 5 x 104 Dm (B) (33/4) x 104 Dm (C) (65/4) x 104 Dm (D) (5/4) x 104 Dm
36. নীচের চিত্রের মতো চারটি একই রকম পাত d দূরত্ব অন্তর রাখা হল । প্রতিটি পাতের ক্ষেত্রফল a । পাতগুলি চিত্রের বর্তনী অনুযায়ী সংযুক্ত । তাহলে P এবং Q -র মধ্যে ধারকত্ব হবে ?

(A) 2aϵ0/d (B) aϵ0/(2d) (C) aϵ0/d (D) 4aϵ0/d
37. দীর্ঘদৃষ্টি ত্রুটিসম্পন্ন (longsighted) এক ব্যক্তির স্পষ্ট দর্শনের নুন্যতম দূরত্ব 60 cm । চশমা ব্যবহার করলে এই নুন্যতম দূরত্ব হয় 12 cm । এই চশমার ক্ষমতা হল
(A) +5.0 D (B) +(20/3) D (C) -(10/3) (D) D +2.0 D
38. একটি বস্তুকণার ওপর স্থির মানের যান্ত্রিক ক্ষমতা প্রয়োগ করা হচ্ছে । এর ফলে নীচের কোন ভৌত রাশিটি ধ্রুবক হবে ?
(A) দ্রুতি (B) ত্বরণের পরিবর্তনের হার (C) গতিশক্তি (D) গতিশক্তির পরিবর্তনের হার
39. M ভর ও q আধান বিশিষ্ট একটি বস্তুকণা স্থির অবস্থায় আছে । কণাটিকে একটি সুষম তড়িৎক্ষেত্র E দ্বারা D দূরত্ব পর্যন্ত ত্বরান্বিত করা হল এবং তারপরে সেটি সরাসরি একই চিহ্নের একটি স্থির আধান Q -এর দিকে ধাবিত হল । q আধানটি যখন সর্বাপেক্ষা নিকটবর্তী হবে তখন সেই দূরত্বটি দাঁড়াবে
(A) qQ4πϵ0D (B) Q4πϵ0ED (C) qQ2πϵ0D2 (D) Q4πϵ0E
40. একটি n-p-n ট্রানজিস্টারের ক্ষেত্রে
(A) সংগ্রাহকের (collector) তুলনায় নিঃসারকের (emitter) ডোপিং -এর মাত্রা বেশি হয়
(B) নিঃসারকের তুলনায় সংগ্রাহকের ডোপিং -এর মাত্রা কম হবে
(C) নিঃসারক ও সংগ্রাহক উভয়ের ডোপিং -এর মাত্রা সমান হবে
(D) ভূমি (base) অঞ্চলটিতে ডোপিং -এর মাত্রা সর্বাপেক্ষা বেশি হয়
41. দুটি ভিন্ন স্থানে বিনতি কোণগুলি হল যথাক্রমে 30° এবং 45° । ওই দুটি স্থানের ভু-চৌম্বক ক্ষেত্রের অনুভূমিক উপাংশগুলির অনুপাত হবে
(A) √3 : √2 (B) 1 : √2 (C) 1 : 2 (D) 1 : √3
42. →A=ˆi+2ˆj+2ˆk এবং →B=3ˆi+6ˆj+2ˆk দুইটি ভেক্টর রাশি দেওয়া আছে । অপর একটি ভেক্টর রাশি →C -এর মান →B -এর মানের সমান কিন্তু তার অভিমুখ →A -এর অভিমুখ বরাবর । নিম্নলিখিত কোন ভেক্টর রাশিটি →C হবে ?
(A) 73(ˆi+2ˆj+2ˆk) (B) 37(ˆi−2ˆj+2ˆk) (C) 79(ˆi−2ˆj+2ˆk) (D) 97(ˆi+2ˆj+2ˆk)
43. তিনটি সুষম পরিবাহী তার (AB, BC, CA) -এর সাহায্যে একটি সমবাহু ত্রিভুজ গঠন করা হল । তড়িৎপ্রবাহ (I) A বিন্দু দিয়ে প্রবেশ করে এবং BC -র মধ্যবিন্দু দিয়ে নির্গত হয় । যদি ত্রিভুজের প্রতি বাহুর দৈর্ঘ্য L হয়, তাহলে ত্রিভুজের কেন্দ্রে O চৌম্বক ক্ষেত্র B হল
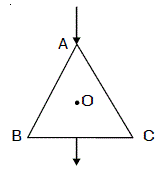
(A) μ04π(4IL) (B) μ02π(4IL) (C) μ04π(2IL) (D) Zero
44. 17 ms-1 গতিতে চলমান একটি মোটর গাড়ির দিকে একটি বাস এগিয়ে চলেছে । বাসটির হর্নের কম্পাঙ্ক 640 Hz কিন্তু মোটর গাড়ির চালকের কাছে সেই কম্পাঙ্ক 680 Hz বলে মনে হচ্ছে । যদি বায়ুতে বাতাসের গতিবেগ 340 ms-1 হয়, তাহলে বাসটির গতিবেগ হল
(A) 2 ms-1 (B) 4 ms-1 (C) 8 ms-1 (D) 10 ms-1
45. একটি বস্তুকণা সুষম দ্রুতি v নিয়ে r ব্যাসার্ধের O কেন্দ্র বিশিষ্ট একটি বৃত্তাকার পথে ঘুরছে । এই বৃত্তাকার পথে P এবং Q দুটি বিন্দু আছে এবং দেওয়া আছে ∠POQ=θ । তা হলে P থেকে Q পর্যন্ত পৌঁছুতে কণাটির গতিবেগের পরিবর্তনের মান হবে
(A) 2vsin(2θ) (B) Zero (C) 2vsin(θ2) (D) 2vcos(θ2)
Q. 46 – Q. 55 carry two marks each, for which only one option is correct. Any wrong answer will lead to deduction of 2/3 mark
46. দুটি সরল দোলগতির সমীকরণ যথাক্রমে
x1=asinωt+acosωt এবং x2=asinωt+a√3cosωt
প্রথম ও দ্বিতীয় গতির বিস্তারের অনুপাত এবং তাদের গতির মধ্যে দশা পার্থক্য হল যথাক্রমে
(A) √32 এবং π12 (B) √32 এবং π12 (C) 2√3 এবং π12 (D) √32 এবং π6
47. L প্রাথমিক দৈর্ঘ্যবিশিষ্ট নগণ্য ভরের একটি স্প্রিং -এর এক প্রান্তে m ভরের বস্তুকণাকে যুক্ত করলে উলম্ব রেখার তার কম্পনের জন্য স্প্রিং -এর কৌণিক কম্পাঙ্ক হয় ω0 । স্প্রিং -এর এক প্রান্তকে স্থির রেখে ও অন্যপ্রান্তে একই ভরকে সংযুক্ত করে অনুভূমিক তলে ω সমকৌণিক বেগে ঘোরানো হল । তাহলে এক্ষেত্রে স্প্রিং -এর দৈর্ঘ্য প্রসারণ হবে
(A) ω2Lω20−ω2 (B) ω20Lω2−ω20 (C) ω2Lω20 (D) ω20Lω2
48. একটি পাত্রে রাখা ρ1 ঘনত্বের তরলের মধ্যে একটি চোঙাকৃতি বস্তু উলম্ব ভাবে ভাসমান । এই অবস্থায় বস্তুর আয়তনের x1 অংশ তরলে নিমজ্জিত আছে । এবারে পাত্রের মধ্যে ρ2 ঘনত্বের আর একটি তরল (ρ2<ρ1) ঢালা হল যাতে বস্তুটি ঠিক পূর্ণ নিমজ্জিত অবস্থায় তরলদ্বয়ের মধ্যে ভাসমান থাকে এবং এক্ষেত্রে বস্তুর আয়তনের x2 অংশ ρ1 ঘনত্বের তরলের মধ্যে নিমজ্জিত থাকে । তা হলে ρ1/ρ2 হবে
(A) 1−x2x1−x2 (B) 1−x1x1+x2 (C) x1−x2x1+x2 (D) x2x1−1
49. R ব্যাসার্ধের একটি তড়িতাহিত গোলকের আধানের আয়তন ঘনত্ব ρ=kr যেখানে r হচ্ছে কেন্দ্র থেকে গোলকের মধ্য কোনো বিন্দুর দূরত্ব এবং k = ধ্রুবক । সেক্ষেত্রে গোলকের উপরিপৃষ্ঠে তড়িৎক্ষেত্রের মান হল (ε0 = শূন্য মাধামের তড়িৎভেদ্যতা)
(A) 4πkR43ϵ0 (B) kR3ϵ0 (C) 4πkRϵ0 (D) kR24ϵ0
50. q আধানবিশিষ্ট M ভরের একটি বস্তুকণা 2d দূরত্বের ব্যবধানে রাখা দুটি স্থির একই ধরনের আধানের (প্রতিটি আধানের মান = Q) মধ্যবিন্দুতে স্থির অবস্থায় আছে । স্থির আধানদুটির সংযোগকারী সরলরেখা বরাবর বস্তুকণাটিকে x দূরত্ব (x << d) সরিয়ে ছেড়ে দেওয়া হল । বস্তুকণাটি এর ফলে সরল দোলগতি সম্পন্ন করবে যার পর্যায়কাল হবে (ε0 = শূন্য মাধামের তড়িৎভেদ্যতা)
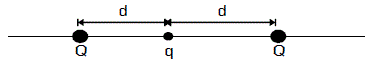
(A) 2√π3Mϵ0dQq (B) 2√π2Mϵ0d3Qq (C) 2√π3Mϵ0d3Qq (D) 2√π3Mϵ0Qqd3
51. একটি বস্তুকে ভূমি থেকে →v=(3ˆi+10ˆj) ms-1 বেগে নিক্ষেপ করা হল । বস্তুটির সর্বাধিক উচ্চতা ও প্রক্ষেপসীমা যথাক্রমে ( g = 10 ms-2)
(A) 5 m এবং 6 m (B) 3 m এবং 10 m (C) 6 m এবং 5 m (D) 3 m এবং 5 m
52. কোনো ধাতবপৃষ্ঠে V1 কম্পাঙ্কের একবর্ণী আলো ফেলা হলে নির্গত ফটো ইলেকট্রনের নিবৃত্তি বিভব হয় V1 । একই ধাতব পৃষ্ঠে অন্য একটি কম্পাঙ্কের একবর্ণী আলো ফেলা হলে নিবৃত্তি বিভব V2 হয় । তাহলে দ্বিতীয় ক্ষেত্রে আলোর কম্পাঙ্ক হল (e = ইলেকট্রনের আধান, h = প্ল্যাঙ্কের ধ্রুবক)
(A) V1−eh(V2+V1) (B) V1+eh(V2+V1) (C) V1−eh(V2−V1) (D) V1+eh(V2−V1)
53. E তড়িচ্চালক বল বিশিষ্ট একটি কোশের সঙ্গে R1 রোধ যুক্ত করলে t সময়ের অবকাশে তার মধ্যে H তাপ উত্পন্ন হয় । R1 -এর পরিবর্তে কোশের সঙ্গে R2 রোধ যুক্ত করলে একই সময় t -এর অবকাশে এই রোধটির মধ্যে 4H তাপ উত্পন্ন হয় । তাহলে কোশের অভ্যন্তরীন রোধ হল
(A) 2R1+R22 (B) √R1R22√R2−√R1√R2−2√R1 (C) √R1R2√R2−2√R12√R2−√R1 (D) √R1R2√R2−√R1√R2+√R1
54. 3 মোল এক পরমাণুক গ্যাস (γ = 5/3) এবং এক মোল দ্বিপরমাণুক গ্যাস (γ = 7/3) মেশানো হল । মিশ্রণে γ -এর মান হবে
(A) 9/11 (B) 11/7 (C) 12/7 (D) 15/7
55. r ব্যাসার্ধের এবং R রোধ বিশিষ্ট একটি বৃত্তাকার পরিবাহীর তলের সঙ্গে লম্বভাবে একটি চৌম্বক ক্ষেত্র B = 2t + 4t² (যেখানে t = সময় ) প্রয়োগ করা হল । t = 0s থেকে t = 2s সময়ের মধ্যে বৃত্তাকার পরিবাহীর মধ্যে যে তাড়িতাধান প্রবাহিত হবে তা হল (সমস্ত একক SI -তে আছে ধরে নিয়ে)
(A) 6πr2R (B) 20πr2R (C) 32πr2R (D) 48πr2R
Q. 56 – Q. 60 carry two marks each, for which one or more than one options may be correct. Marking of correct options will lead to a maximum mark of twoon pro rata basis. There willbe no negative marking for these questions. However, any marking of wrong option will lead to award of zero mark against the respective question – irrespective of the number of corredt options marked.
56. কোনো অঞ্চলে তড়িৎক্ষেত্র ও চৌম্বকক্ষেত্রের মান যথাক্রমে E এবং B । যে যে সম্ভাবনাগুলির জন্য কোনো তড়িতাধান ওই অঞ্চলে সমগতিবেগ v -তে চলতে পারে তা হল
(A) E = vB (B) E ≠ 0, B = 0 (C) E = 0, B ≠ 0 (D) E ≠ 0, B ≠ 0
57. e আধান বিশিষ্ট ও m ভর বিশিষ্ট একটি ইলেকট্রন ω সমকৌণিক দ্রুতিতে r ব্যাসার্ধের বৃত্তপথে ঘুর্ণায়মান । তা হলে নীচের বিবৃতি গুলির কোনগুলি সঠিক ?
(A) বৃত্তাকার পথে তড়িৎপ্রবাহ r² এর সমানুপাতিক
(B) বৃত্তাকার পথে তড়িৎপ্রবাহের জন্য চৌম্বক ভ্রামক m -এর ওপর নির্ভরশীল নয়
(C) চৌম্বক ভ্রামকের মান হল ইলেকট্রনের কৌণিক ভরবেগের 2e/m গুণ
(D) ইলেকট্রনের কৌণিক ভরবেগ ইলেকট্রনের ক্ষেত্রীয় গতিবেগের সমানুপাতিক
58. একটি উভোত্তল লেন্সের ফোকাস দৈর্ঘ্য f এবং উভয় পৃষ্ঠের বক্রতা ব্যাসার্ধ R । লেন্সটির উপাদানের প্রতিসরাঙ্ক n1 এবং লেন্সটিকে n2 প্রতিসরাঙ্ক বিশিষ্ট একটি তরলে নিমজ্জিত করা হল । এখন লেন্সটি
(A) কেবলমাত্র R -এর ওপর নির্ভর করে উত্তল বা অবতল লেন্সের মতো আচরণ করবে
(B) n1 এবং n2 -এর ওপর নির্ভর করে উত্তল লেন্সের মতো আচরণ করবে
(C) n1 এবং n2 -এর ওপর নির্ভর করে অবতল লেন্সের মতো আচরণ করবে
(D) R, n1 এবং n2 -এর মান যাই হোক না কেন লেন্সটি একই ফোকাল দৈর্ঘ্যের উত্তল লেন্স হিসাবে আচরণ করবে
59. ঘর্ষণহীন এবং নগণ্য ভরের একটি স্থির কপিকলের ওপর দিয়ে নগণ্য ভরের অপ্রসার্য একটি সুতোর একপ্রান্তে একটি ব্লককে (ভর m = 0.1 kg) ঝোলানো হয়েছে । সুতোর অপর প্রান্তটিকে একটি স্থির বল F দ্বারা উলম্ব ভাবে নীচের দিকে টানা হচ্ছে । ব্লকটি স্থির অবস্থা থেকে ওপরের দিকে উঠতে শুরু করলে ব্লকটির রৈখিক ভরবেগ 1s -এ 2 kg ms-1 পরিবর্তিত হয় । (প্রদত্ত g = 10 ms-2)
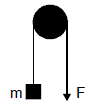
(A) সুতোর টান হল F
(B) সুতোর টান হল 3N
(C) সুতোর টান কর্তৃক ব্লকের ওপর 1s -এর কার্য হল 20 J
(D) অভিকর্ষজ বলের বিরুদ্ধে ব্লক কর্তৃক কৃত কার্য হল 10 J
60. l দৈর্ঘ্যের একটি সুষম দন্ডের এক প্রান্তে একটি m ভরের বস্তুকণা যুক্ত করে ω সমকৌণিক দ্রুতিতে দন্ডের মধ্যবিন্দুকে কেন্দ্র করে সেটিকে উলম্ব তলে ঘোরানো হচ্ছে । ঘুর্ণনের কোনো এক মুহুর্তে যখন দন্ডটি অনুভূমিক, তখন m ভরটি দন্ডটি থেকে ছিন্ন হল, কিন্তু দন্ডটি একই ω কৌণিক দ্রুতিতে ঘুরতে লাগল । দন্ডটি থেকে ছিন্ন হওয়ার পরে m ভরটি উলম্বদিকে উঠল এবং আবার একই উলম্বপথে গিয়ে দন্ডের একই অনুভূমিক অবস্থানে যুক্ত হল । g ওই স্থানের অভিকর্ষজ ত্বরণ হলে
(A) এই ঘটনা সম্ভব হবে যদি ω2l2πg রাশিটি একটি পূর্ণ সংখ্যা হয়
(B) বস্তুটির মোট উত্পতন কাল ω² -এর সমানুপাতিক হয়
(C) বস্তুটির বায়ুতে মোট অতিক্রান্ত দূরত্ব ω² -এর সমানুপাতিক হয়
(D) বস্তুটির কর্তৃক বায়ুতে অতিক্রান্ত দূরত্ব এবং উত্পতন কাল উভয়েই বস্তুর ভরের ওপর নির্ভরশীল নয়
***