লম্ব-বৃত্তাকার চোঙ

লম্ব-বৃত্তাকার চোঙ (Right-circular Cylinder)

সূচনা (Introduction) :- বাস্তবক্ষেত্রে আমরা প্রায় চোঙাকৃতি ঘনবস্তু দেখতে পাই, যেমন রড, নল, চক, জলের পাইপ, বেলেন ইত্যাদি । এই সমস্ত বস্তুগুলির আয়তন, পরিমাপ ইত্যাদি জানতে হলে আমাদের কাছে এই অধ্যায়টি খুবই গুরুত্বপূর্ণ । 

সংজ্ঞা (Definition) :-  কোনো আয়তক্ষেত্রের একটি বাহুকে অক্ষ ধরে আয়তক্ষেত্রটিকে ওই বাহুর চারিদিকে একবার পূর্ণ আবর্তন করালে যে ঘনবস্তু উৎপন্ন হয় তাকে লম্ব বৃত্তাকার চোঙ (Right-circular Cylinder) বলে । 

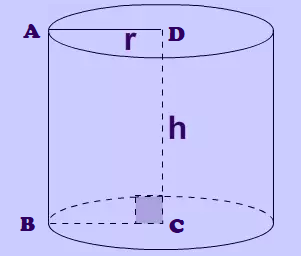
উপরের চিত্রটিতে ABCD আয়তক্ষেত্রটির DC বাহুকে অক্ষ ধরে আয়তক্ষেত্রটিকে একবার আবর্তন করলে, আবর্তনের ফলে একটি চোঙ উৎপন্ন হয়েছে । AB বাহুকে চোঙটির উৎপাদক রেখা (Generating line) বলা হয় । D এবং C বিন্দু দুটি যথাক্রমে A এবং B থেকে সমদূরত্ব বজায় রেখে একবার আবর্তন করায় চোঙটির উপরে এবং নীচে দুটি সর্বসম বৃত্তাকার তল তৈরী হয়েছে, যার ব্যাসার্ধ যথাক্রমে AD এবং BC .নীচের তলটিকে চোঙের ভূমি (Base of Cylinder) বলে , ভূমিতলের পরিধি বরাবর ভূমিতলের উপর লম্বভাবে দন্ডায়মান বক্রতলটি যা চোঙটির চারপাশ ঘিরে আছে তাকে চোঙের পার্শ্বতল (Side Base of Cylinder) বলে । চোঙের তিনটি তলের দুটি সমতল ও একটি বক্রতল । DC অক্ষটির দৈর্ঘ্যকে চোঙের উচ্চতা (Height) বলা হয় । 

এখন আমরা যদি চোঙটিকে AB বরাবর কাটি, তবে একটি আয়তকার তল পাব । যার দৈঘ্য চোঙটির ভূমির পরিধি এবং প্রস্ত হল চোঙের উচ্চতা । 

লম্ব বৃত্তাকার চোঙের তলসমূহের ক্ষেত্রফল এবং আয়তন নির্ণয় (Calculate the Area and Volume of Right-circular Cylinder)

এখানে  চোঙটির বৃত্তাকার তল দুটির ব্যাসার্ধ হল AD = r ও BC = r এবং উচ্চতা DC = h  ।

অতএব চোঙটির ভূমির ক্ষেত্রফল = [tex]\pi {r^2}[/tex] বর্গএকক 

চোঙটির পার্শ্বতলের ক্ষেত্রফল

= ( ভূমির পরিধি [tex] \times [/tex] উচ্চতা ) বর্গএকক

= [tex]2\pi rh[/tex] বর্গএকক

চোঙটির সমগ্রতলের ক্ষেত্রফল

= ( 2 [tex] \times [/tex] ভূমির ক্ষেত্রফল + চোঙটির পার্শ্বতলের ক্ষেত্রফল ) বর্গএকক

= [tex]2\pi {r^2} \times 2\pi rh[/tex] বর্গএকক

= [tex]2\pi r\left( {r + h} \right)[/tex] বর্গএকক

চোঙটির ঘনফল বা আয়তন 

= ( ভূমির ক্ষেত্রফল [tex] \times [/tex] উচ্চতা ) ঘনএকক 

= [tex]\pi {r^2}h[/tex] ঘনএকক

কোনো ফাঁপা চোঙের বাইরের ব্যাসার্ধ [tex]{r_1}[/tex] ভিতরের ব্যাসার্ধ [tex]{r_2}[/tex] এবং উচ্চতা h হলে ফাঁপা চোঙটির ঘনফল বা আয়তন [tex] = \pi \left( {{r_1}^2 - {r_2}^2} \right)h[/tex] 

চোঙটির ভিতরে ও বাইরে বক্রতলের মোট ক্ষেত্রফল [tex] = 2\pi \left( {{r_1} + {r_2}} \right)h[/tex] .