পিথাগোরাসের উপপাদ্য (Pythagoras Theorem)
পিথাগোরাসের উপপাদ্য :- কোনো সমকোণী ত্রিভুজের অতিভুজের ওপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর ওপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টির সমান ।
ধরা যাক ABC একটি সমকোণী ত্রিভুজ যার ∠A সমকোণ ।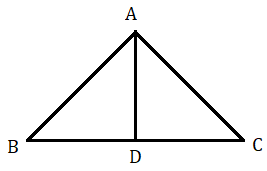
প্রমাণ করতে হবে BC2=AB2+AC2
অঙ্কন : সমকৌনিক বিন্দু A থেকে অতিভুজ BC এর উপরে AD লম্ব অঙ্কন করা হল যা BC বাহুকে D বিন্দুতে ছেদ করে ।
প্রমাণ : সমকোণী ত্রিভুজ ABC এর অতিভুজ BC এর উপরে AD লম্ব ।
অতএব ত্রিভুজ ABD ও ত্রিভুজ ABC সদৃশ
সুতরাং ABBC=BDAB⇒AB2=BD⋅BC ......(i)
আবার ত্রিভুজ CAD ও ত্রিভুজ CBA সদৃশ
সুতরাং ACBC=DCAC⇒AC2=BC⋅DC.............(ii)
এখন (i) + (ii) করে পাই
AB2+AC2=BD⋅BC+BC⋅DC=BC⋅(BD+DC)=BC⋅BC=BC2
অতএব প্রমাণিত BC2=AB2+AC2
আজ থেকে অনেক পূর্বে ( প্রায় 800 BC ) একজন প্রাচীন ভারতীয় গণিতজ্ঞ বৌদ্ধায়ন পিথাগোরাসের উপপাদ্যটিকে নিন্মরূপে বলেছিলেন । তিনি বলেছিলেন একটি আয়তকার চিত্রের কর্ণের উপর বর্গক্ষেত্রের ক্ষেত্রফল উহার উভয় বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলের সমষ্টির সমান ।
[ The diagonal of a rectangle produces by itself the same area as produced by its both sides ( i.e length and breath )]
এই জন্য এই উপপাদ্যটিকে কখনও কখনও বৌদ্ধায়নের উপপাদ্য বলা হয় ।
পিথাগোরাসের উপপাদ্যের বিপরীত উপপাদ্য :- কোনো ত্রিভুজের একটি বাহুর ওপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর ওপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টির সমান হলে, ত্রিভুজটি সমকোণী হবে, যার বৃহত্তম বাহুর বিপরীত কোণ সমকোণ হবে ।
মনে করি ABC ত্রিভুজের AB বাহুর উপরে অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল BC ও AC বাহুর উপরে অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টির সঙ্গে সমান। অর্থাৎ , AB2=BC2+AC2
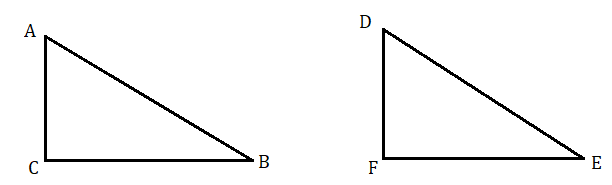
প্রমাণ করতে হবে ∠ACB=90∘ = 1 সমকোণ
অঙ্কন : CB এর সমান করে FE সরলরেখা অঙ্কন করলাম। FE বাহুর উপরে F বিন্দুতে লম্ব অঙ্কন করলাম এবং সেই লম্ব থেকে CA বাহুর সমান করে FD অংশ কেটে নিলাম এবং DE বিন্দুদ্বয় যোগ করলাম।
প্রমাণ :
AB2=BC2+AC2=EF2+DF2
( যেহেতু অঙ্কনানুসারে EF = BC এবং AC = DF )
=DE2
এখন ত্রিভুজ ABC ও ত্রিভুজ DEF এর AB = DE , BC = EF এবং AC = DF
অতএব ত্রিভুজ ABC ≅ ত্রিভুজ DEF
অতএব ∠ACB=∠DFE=90∘= 1 সমকোণ ( যেহেতু DF⊥EF অঙ্কনানুসারে )
অতএব ∠ACB=90∘ = 1 সমকোণ
উদাহরণ 1. ABC সমকোণী ত্রিভুজের ∠ABC = এক সমকোণ এবং AB=5 সেমি এবং BC=12 সেমি । ABC ত্রিভুজের পরিবৃত্তের ব্যাসার্ধ কত ?
সমাধান : যেহেতু ∠ABC = এক সমকোণ, সুতরাং AC হল △ABC -এর পরিবৃত্তের ব্যাস । এখন সমকোণী ত্রিভুজ ABC থেকে পাই —
AC2=BC2+AB2=(12)2+52=144+25
=169=(13)2
∴AC=13
∴△ABC-এর পরিব্যাসার্ধ =132 সেমি = 6.5 সেমি.
উদাহরণ 2. ABC সমকোণী ত্রিভুজের ∠B সমকোণ এবং BD⊥AC হলে নীচের সম্পর্কগুলির মধ্যে কোনটি সঠিক হবে ?
(i) BC2+DC2=AC2
(ii) AB2−BC2=AD2−CD2
(iii) BC2−BD2=AB2−AD2
সমাধান : △ABD সমকোণী ত্রিভুজ
∴AB2=BD2+AD2
আবার সমকোণী ত্রিভুজ BCD-এর BC2=BD2+CD2
∴AB2−BC2=(BD2+AD2)−(BD2+CD2)=AD2−CD2
∴ (ii) সম্পর্কটি সঠিক ।
*****