বাস্তব সংখ্যা (Real Number)
সূচনা (Introduction) :-
গণিতে আমরা সাধারণত পাটিগণিত, বীজগণিত, জ্যামিতি, স্থানাঙ্ক জ্যামিতি এবং ত্রিকোণমিতি সম্পর্কে শিখেছি । এদের মধ্যে বিষয়গত কিছু পার্থক্য থাকলেও এইসব বিষয়ের আলোচনা মূলত সংখ্যা ও গণিতের মূলত চারটি প্রক্রিয়াকে (অর্থাৎ যোগ, বিয়োগ, গুণ এবং ভাগ) ভিত্তি করে গড়ে উঠেছে । কলনবিদ্যায় সংখ্যা ও চারটি মূলগত প্রক্রিয়া ছাড়াও নতুন ধারণা (অসীম, অপেক্ষক ও সীমার ধারণা) প্রয়োগ করা হয় । এই নতুন মূলগত ধারণা গুলি একটি সংখ্যাশ্রেণিকে ভিত্তি করে গড়ে উঠেছে । এই সংখ্যাশ্রেণিকে বাস্তব সংখ্যাশ্রেণি বলা হয় । এই সংখ্যা শ্রেণির সাহায্যে যেকোনো দৈর্ঘ্য পরিমাপ সম্ভব এবং এর মধ্যে গণিতের মূলত চারটি প্রক্রিয়া (অর্থাৎ যোগ, বিয়োগ, গুণ ও ভাগ) প্রয়োগ করা যায় ও প্রক্রিয়াগুলির সাপেক্ষে সংখ্যশ্রেণিটি বদ্ধ (closed), অর্থাৎ প্রক্রিয়াগুলির প্রয়োগে যে ফল পাওয়া যায় তা ওই সংখ্যশ্রেণির অন্তর্গত হয় ।
সংখ্যা (Number)
উচ্চতর গণিতে সংখ্যা সম্পর্কে বিস্তারিত ভাবে আলোচনা করা হয়েছে এখানে আমরা শুধুমাত্র কলনবিদ্যায় প্রয়োজনীয় বিষয় সম্পর্কে আলোচনা করবো।
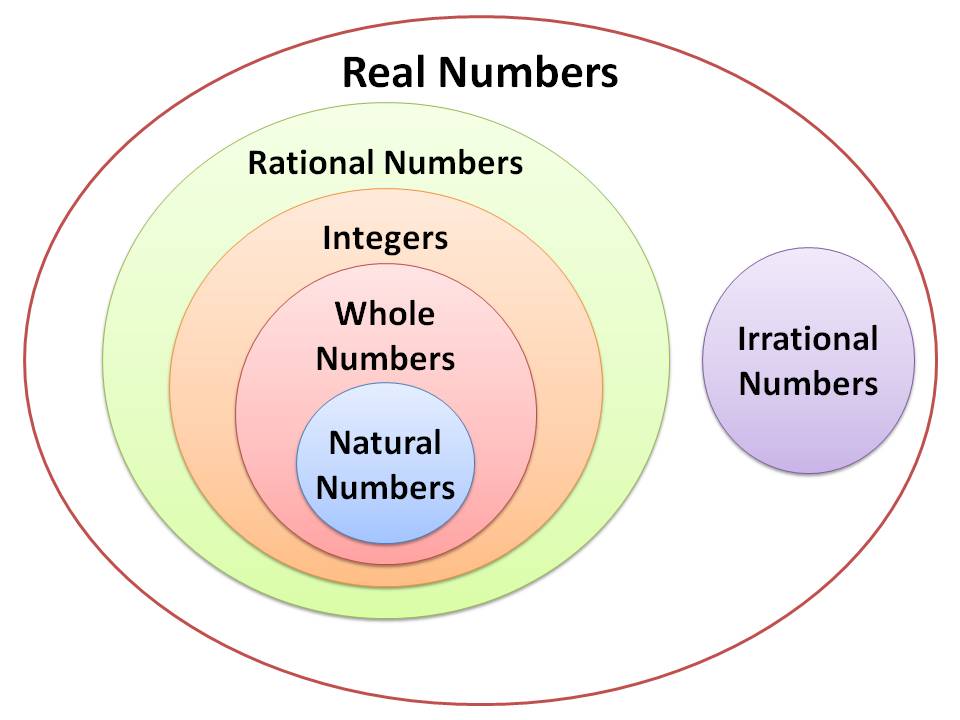
স্বাভাবিক সংখ্যা (Natural Number)
সংজ্ঞা (Definition) :- বস্তুসমূহ গণনার প্রয়োজনে 1 , 2 , 3 , 4 , ........... সংখ্যা সমূহের উৎপত্তি হয় এবং এইসব সংখ্যাকে স্বাভাবিক সংখ্যা (Natural Number) বলা হয় ।
স্বাভাবিক সংখ্যার সেটকে N দ্বারা সূচিত করা হয় , অর্থাৎ
[tex]N = \left\{ {1,2,3,4.............} \right\}[/tex] অথবা N = { x : x একটি স্বাভাবিক সংখ্যা }
যে স্বাভাবিক সংখ্যা 1 এবং ওই সংখ্যা ছাড়া অন্য কোনো সংখ্যা দ্বারা বিভাজ্য নয় তাকে মৌলিক সংখ্যা (Prime Number) বলে । যেমন 2, 3, 5, 7, 11 ইত্যাদি । এই সমস্ত সংখ্যাগুলি 1 ও ওই সংখ্যা ব্যাতিত অন্য কোনো সংখ্যা দ্বারা বিভাজিত হয় না । অন্যভাবে যে স্বাভাবিক সংখ্যা 1 এবং ওই সংখ্যা ব্যাতিত অন্য সংখ্যা দ্বারা বিভাজ্য হয় তাকে যৌগিক সংখ্যা (Composite Number) বলে । যেমন 4, 6, 10 ইত্যাদি । 4 সংখ্যাটি 1, 2 এবং 4; 6 সংখ্যাটি 1, 2, 3 এবং 6 ও 10 সংখ্যাটি 1, 2, 5 এবং 10 দ্বারা বিভাজ্য অর্থাৎ 1 এবং ওই সংখ্যা ছাড়াও অন্যান্য সংখ্যা দ্বারা বিভাজিত হয়েছে । দুটি স্বাভাবিক সংখ্যার মধ্যে যদি 1 ব্যাতিত অন্য কোনো উৎপাদক না থাকে তবে সংখ্যা দুটিকে পরস্পরের মৌলিক সংখ্যা (Prime to each other) বলে । যেমন 4 এবং 9 এরা পরস্পরের মৌলিক সংখ্যা কারণ এরা নিজেরা মৌলিক সংখ্যা না হলেও এদের মধ্যে 1 ব্যাতিত আর অন্য কোনো উৎপাদক নেই ।
স্পষ্টত দেখা যাচ্ছে যে যোগ ও গুণ প্রক্রিয়ার ক্ষেত্রে স্বাভাবিক সংখ্যা বদ্ধ, অর্থাৎ দুই বা ততোধিক স্বাভাবিক সংখ্যার যোগফল অথবা গুণফল একটি স্বাভাবিক সংখ্যা হয় (যেমন 4 + 7 = 11 এবং [tex]4 \times 7 = 28[/tex]) । কিন্তু বিয়োগ বা ভাগের ক্ষেত্রে স্বাভাবিক সংখ্যা বদ্ধ নয়, অর্থাৎ দুটি স্বাভাবিক সংখ্যার মধ্যে বিয়োগফল বা ভাগফল একটি স্বাভাবিক সংখ্যা নাও হতে পারে (যেমন 4 - 7 = -3 এবং [tex]4 \div 7 = \frac{4}{7}[/tex]) ।
পূর্ণসংখ্যা বা অখন্ড সংখ্যা (Integers)
সংজ্ঞা (Definition) :- স্বাভাবিক সংখ্যাসমূহের সঙ্গে 0, -1, -2, -3, ..........সংখ্যা সমূহের সংযোজন করে যেসব সংখ্যা পাওয়া যায় তাদের পূর্ণসংখ্যা বা অখন্ড সংখ্যা (Integers) বলে ।
পূর্ণসংখ্যার সেটকে সাধারণত I দ্বারা সূচিত করা হয় ; অর্থাৎ
[tex]I = \left\{ {0, \pm 1, \pm 2,.............} \right\}[/tex] অথবা I = {a : a একটি পূর্ণসংখ্যা}
পূর্ণসংখ্যা সেটের 1, 2, 3, .......... সংখ্যাগুলিকে বলা হয় ধনাত্মক পূর্ণসংখ্যা (Positive Integers) এবং -1, -2, -3, .......... সংখ্যাগুলিকে বলা হয় ঋণাত্মক পূর্ণসংখ্যা (Negative Integers) । ধনাত্মক পূর্ণসংখ্যার সেটকে [tex]{I^ + }[/tex] এবং ঋণাত্মক পূর্ণসংখ্যার সেটকে [tex]{I^ - }[/tex] দ্বারা সূচিত করা হয় । অর্থাৎ
[tex]{I^ + } = \left\{ {1,2,3,..........} \right\};{I^ - } = \left\{ { - 1, - 2, - 3,.........} \right\}[/tex]
যেসমস্ত পূর্ণসংখ্যা দুই দ্বারা বিভাজ্য তাদের জোড় বা যুগ্ম পূর্ণসংখ্যা (even integer) বলা হয় । যেমন [tex] \pm 2, \pm 4, \pm 6,.........[/tex] . শূন্যকে একটি যুগ্ম সংখ্যা হিসাবে ধরা হয় । n যেকোনো একটি পূর্ণসংখ্যা হলে 2n সর্বদা যুগ্ম পূর্ণসংখ্যা হবে । যে সমস্ত পূর্ণসংখ্যা দুই দ্বারা বিভাজ্য হয় না তাদেরকে বিজোড় বা অযুগ্ম পূর্ণসংখ্যা (odd integer) বলা হয় । যেমন [tex] \pm 1, \pm 3, \pm 5,.......[/tex]. n যে কোনো পূর্ণসংখ্যা হলে (2n + 1) বা (2n - 1) সর্বদা অযুগ্ম পূর্ণসংখ্যা হবে ।
সহজেই বোঝা যায় যে যোগ, বিয়োগ এবং গুণ এর ক্ষেত্রে পূর্ণসংখ্যার সেট বদ্ধ । অর্থাৎ যোগ, বিয়োগ এবং গুণের ক্ষেত্রে যে ফল পাওয়া যায় তা পূর্ণসংখ্যা সেটের অন্তর্গত । কিন্তু ভাগের ক্ষেত্রে যে ভাগফল পাওয়া যায় তা সর্বদা পূর্ণসংখ্যা সেটের অন্তর্গত হয়না, যেমন [tex]2 \div 3 = \frac{2}{3}[/tex] .
মূলদ সংখ্যা (Rational Numbers)
সংজ্ঞা ( Definition ):- p এবং q [tex]\left( { \ne 0} \right)[/tex] দুটি পূর্ণ সংখ্যা হলে [tex]\frac{p}{q}[/tex] আকারে প্রকাশিত সংখ্যা মূলদ সংখ্যা (Rational Number) বলে । এখানে p ধনাত্মক বা ঋণাত্মক পূর্ণ সংখ্যা অথবা শূন্য হতে পারে এবং q সর্বদা স্বাভাবিক সংখ্যা হবে ।
p ও q কে পরস্পরের মৌলিক ধরা হয় । অর্থাৎ 1 ব্যাতিত এদের মধ্যে অন্য কোনো উৎপাদক থাকবে না । যদি অন্য কোনো উৎপাদক থাকে তবে তা অপসারণ করে তাকে নিম্নরূপ আকারে প্রকাশ করা হয় । যেমন [tex]\frac{5}{1}, - \frac{3}{1},\frac{3}{4},\frac{{12}}{{15}} = \frac{4}{5}[/tex] .
মূলদ সংখ্যার সেটকে সাধারণত Q দ্বারা সূচিত করা হয়। অর্থাৎ
[tex]Q = \left\{ {\frac{p}{q}:p \in I,q \in N} \right\}[/tex]
শূন্য দ্বারা ভাগ (Division by Zero)
ধরি a যে কোনো মূলদ সংখ্যা। আমরা জানি [tex]a \times 0 = 0[/tex] ............(i)
স্পষ্টত a এর মান যে কোনো মূলদ সংখ্যা হতে পারে । এখন ভাগের সংজ্ঞানুযায়ী (i) থেকে পাই [tex]\frac{0}{0} = a[/tex] . অর্থাৎ [tex]\frac{0}{0}[/tex] এর মান যে কোনো মূলদ সংখ্যা হতে পারে । সুতরাং শূন্য কে শূন্য দ্বারা ভাগ করলে কোনো অর্থ হয় না অর্থাৎ অনির্ণেয় ।
আবার [tex]a \ne 0[/tex] এবং b দুটি মূলদ সংখ্যা এবং [tex]\frac{a}{b} = 0[/tex] হলে, ভাগের সংজ্ঞানুযায়ী, [tex]a = 0 \times b[/tex]. আবার আমরা জানি [tex]b \times 0 = 0[/tex] .সুতরাং a = 0 যা কল্পনা বিরোধী । সুতরাং [tex]\frac{a}{0}[/tex] এর কোনো অর্থ নেই ।
অর্থাৎ শূন্য দ্বারা ভাগ অসংজ্ঞাত ।
মূলদ সংখ্যার ধর্মাবলি (Properties of Rational Numbers)
(i) চারটি মূলগত প্রক্রিয়া অর্থাৎ যোগ, বিয়োগ, গুণ ও ভাগ (শূন্য দ্বারা ভাগ ছাড়া ) সাপেক্ষে মূলদ সংখ্যা বদ্ধ, অর্থাৎ দুটি মূলদ সংখ্যার যোগফল , বিয়োগফল, গুণফল ও ভাগফল একটি মূলদ সংখ্যার হবে । উদারণস্বরূপ
যোগফল [tex] = \frac{2}{3} + \frac{4}{5} = \frac{{10 + 12}}{{15}} = \frac{{22}}{{15}} = [/tex] মূলদ সংখ্যা
বিয়োগফল [tex] = \frac{2}{3} - \frac{4}{5} = \frac{{10 - 12}}{{15}} = \frac{{ - 2}}{{15}} = [/tex] মূলদ সংখ্যা
গুণফল [tex] = \frac{2}{3} \times \frac{4}{5} = \frac{8}{{15}} = [/tex] মূলদ সংখ্যা
ভাগফল [tex] = \frac{2}{3} \div \frac{4}{5} = \frac{2}{3} \times \frac{5}{4} = \frac{5}{6} = [/tex] মূলদ সংখ্যা
(ii) মূলদ সংখ্যার সেট বিনিময় (commutative) , সংযোগ (associative) এবং বিচ্ছেদ (distributive) সূত্র সিদ্ধ করে । যদি a , b ও c তিনটি মূলদ সংখ্যা হয় তাহলে
(১) a + b = b + a (যোগের বিনিময় নিয়ম) এবং
[tex]a \times b = b \times a[/tex] (গুণের বিনিময় নিয়ম)
(২) ( a + b ) + c = a + ( b + c ) (যোগের সংযোগ নিয়ম) এবং
[tex]\left( {a \times b} \right) \times c = a \times \left( {b \times c} \right)[/tex] (গুণের সংযোগ নিয়ম)
(৩) [tex]\left( {a + b} \right) \times c = \left( {a \times c} \right) + \left( {b \times c} \right)[/tex] এবং
[tex]a \times \left( {b + c} \right) = \left( {a \times b} \right) + \left( {a \times c} \right)[/tex] (বিচ্ছেদ নিয়ম)
(iii) a এবং b দুটি মূলদ সংখ্যা হলে হয় a > b অথবা a = b নাহলে a < b হবে। একে ত্রিভাগ বা ত্রিবিকল্প নিয়ম ( trichotomy law ) বলা হয় ।
(iv) a , b ও c তিনটি মূলদ সংখ্যা এবং [tex]a \ge b,b > c[/tex] হলে a > c হবে। আবার [tex]a \le b,b < c[/tex] হলে a < c হবে । একে ক্রম নিয়ম (order law) বলা হয় ।
(v) মূলদ সংখ্যা সমূহ সর্বত্র নিবিড় (dense) অর্থাৎ দুটি প্রদত্ত মূলদ সংখ্যার মধ্যে অসংখ্য মূলদ সংখ্যা আছে ।
মূলদ সংখ্যার দশমিক আকার (Decimal form of Rational Numbers)
মূলদ সংখ্যাকে দশমিক আকারে প্রকাশ করা যায় । উদাহরণস্বরূপ
[tex]\frac{3}{4} = 0 \cdot 75,\frac{9}{8} = 1 \cdot 125,\frac{{297}}{{40}} = 7 \cdot 425[/tex]............(i)
আবার [tex]\frac{4}{3} = 1 \cdot \dot 3,\frac{5}{7} = 0 \cdot \dot 71428\dot 5,\frac{{22}}{9} = 2 \cdot \dot 4[/tex].......(ii)
স্পষ্টতই (i) প্রদত্ত মূলদ সংখ্যা গুলির দশমিক আকার সসীম (terminating decimal) এবং (ii) মূলদ সংখ্যাগুলির দশমিক আকার আবৃত্ত অসীম (non terminating recurring decimal) .সুতরাং সহজেই বোঝাযায় যেকোনো মূলদ সংখ্যাকে সসীম দশমিকে অথবা আবৃত্ত দশমিকে প্রকাশ করা যায় ।
আবার দেখা যায়
[tex]0 \cdot 375 = \frac{{375}}{{1000}} = \frac{3}{8},2 \cdot 03 = \frac{{203}}{{100}}[/tex]...........(iii)
এবং [tex]2 \cdot \dot 7\dot 3 = \frac{{273 - 2}}{{99}} = \frac{{271}}{{99}},0 \cdot 3\dot 2\dot 5 = \frac{{325 - 3}}{{990}} = \frac{{161}}{{495}}[/tex]............(iv)
স্পষ্টতই (iii) এবং (iv) থেকে বোঝা যায় কোনো সংখ্যা সসীম অথবা আবৃত্ত দশমিকের আকারে থাকলে তাকে মূলদ সংখ্যার আকারে প্রকাশ করা যায় । সুতরাং কোনো সংখ্যাকে যদি সসীম অথবা আবৃত্ত দশমিকের আকারে প্রকাশ করা না যায় তাকে মূলদ সংখ্যা বলা যায় না । উদাহরণস্বরূপ
1. 414213.......... , 2. 1625923.......... এই দুটি সংখ্যার দশমিক আকার অসীম এবং অপৌনঃপুনিক বলে মূলদ সংখ্যা হিসাবে প্রকাশ করা যায় না এদেরকে অমূলদ সংখ্যা বলে ।
অমূলদ সংখ্যা (Irrational Numbers)
সংজ্ঞা ( Definition ):- যে সমস্ত সংখ্যাকে [tex]\frac{p}{q}[/tex] ([tex]p \in I[/tex] এবং [tex]q \in N[/tex])আকারে প্রকাশ করা যায় না অথবা যাদের দশমিক আকার অপৌনঃপুনিক ও অসীম তাকে অমূলদ সংখ্যা (Irrational Numbers) বলা হয় ।
বীজগাণিতিক ও অবীজগাণিতিক সংখ্যা (Algebraic and Non algebraic or Transcendental Numbers)
গণিতে ব্যবহৃত সংখ্যস মূহকে দুই ভাগে ভাগ করা যায় (১) বীজগাণিতিক সংখ্যা, (২) অবীজগাণিতিক সংখ্যা ।
(১) বীজগাণিতিক সংখ্যা :- যে সব সংখ্যাকে কোনো বীজগাণিতিক সমীকরণের মূল হিসাবে পাওয়া যায় তাকে বীজগাণিতিক সংখ্যা বলা হয় । এই সংখ্যা মূলদ বা অমূলদ দুই রকম হতে পারে । যেমন [tex]x - 4 = 0 \Rightarrow x = 4[/tex] আবার [tex]{x^2} = 2 \Rightarrow x = \sqrt 2 [/tex] .
(২) অবীজগাণিতিক সংখ্যা :- ত্রিকোনমিতিতে ব্যবহৃত [tex]\pi [/tex] এবং বীজগণিতে ব্যবহৃত [tex]e[/tex] এই সংখ্যা গুলি কোনো সংখ্যার মূল নয় এদেরকে অবীজগাণিতিক সংখ্যা বলে । এই সংখ্যা কখনো মূলদ হতে পারে না ।
বাস্তব সংখ্যা (Real Numbers)
সংজ্ঞা ( Definition ) :- মূলদ সংখ্যাসমূহের সাথে অমূলদ সংখ্যাসমূহকে যোগ করে যেসব সংখ্যা পাওয়া যায় তাকে বাস্তব সংখ্যা (Real Numbers) বলা হয় ।
বাস্তব সংখ্যার সেটকে R দ্বারা সূচিত করা হয়, অর্থাৎ
R = { x : x একটি বাস্তব সংখ্যা }
মূলদ সংখ্যায় আমরা দেখেছি মূলদ সংখ্যা নিবিড় (dense) । যেকোনো মূলদ সংখ্যাকে সংখ্যাঅক্ষের উপর একটি নির্দিষ্ট বিন্দু ধরা হয় । কিন্তু এতটাও নিবিড় নয় যাতে সংখ্যাঅক্ষের উপর যেকোনো বিন্দু একটি মূলদ সংখ্যা হতে পারে । অন্যভাবে বলা যায় মূলদ সংখ্যা নিবিড় হলেও তাদের মধ্যে ফাঁক আছে । সংখ্যাঅক্ষের উপর দুটি মূলদ বিন্দুর মধ্যে এমন অনেক বিন্দু আছে তারা মূলদ সংখ্যার অন্তর্গত নয় এই সব বিন্দুকে অমূলদ সংখ্যা বলে । সুতরাং সংখ্যাঅক্ষের উপর যেকোনো বিন্দু মূলদ বা অমূলদ সংখ্যা হতে পারে । এখন এমন সংখ্যাগোষ্ঠীর কথা ধরা হল যার প্রত্যেকটি সংখ্যা সংখ্যাঅক্ষের উপর এক একটি বিন্দুকে বোঝায় । এই সংখ্যাগোষ্ঠীকে বাস্তব সংখ্যা গোষ্ঠী বলা হয় । এক্ষেত্রে সংখ্যা অক্ষকে বাস্তব অক্ষ এবং প্রত্যেকটি বিন্দুকে বাস্তব বিন্দু বলে । বাস্তব সংখ্যার এইরকম ধারণাকে ক্যান্টর -ডেডিকিন্ডের (Cantar - Dedekind 's) বলে ।
ক্যান্টর -ডেডিকিন্ডের (Cantar - Dedekind 's):- প্রত্যেক বাস্তব সংখ্যার অনুরূপ কেবল একটি বিন্দু সংখ্যা অক্ষের উপরে থাকবে , বিপরীতক্রমে সংখ্যাঅক্ষের উপরে অবস্থিত প্রত্যেক বিন্দু কেবল একটি বাস্তব সংখ্যাকে প্রকাশ করবে ।
পাটীগণিতীয় অবিচ্ছিন্নতা এবং রৈখিক অবিচ্ছিন্নতা (Arithmetical Continuum and Linear Continuum)
সমগ্র বাস্তব সংখ্যসমূহকে নিয়ে পাটীগণিতীয় অবিচ্ছিন্নতা গঠিত হয় । আবার সংখ্যা অক্ষের উপরে অবস্থিত কোনো বিন্দু (যাদের প্রত্যেকটি পাটীগণিতীয় অবিচ্ছিন্নতার অন্তর্গত একটি বাস্তব সংখ্যাকে প্রকাশ করে) নিয়ে রৈখিক অবিচ্ছিন্নতা গঠিত হয় । দেখা যাচ্ছে পাটীগণিতীয় অবিচ্ছিন্নতা ও রৈখিক অবিচ্ছিন্নতা উভয়ই ফাঁক হীন ।
বাস্তব সংখ্যার ধর্মাবলি (Properties of Real Numbers)
যেহেতু মূলদ সংখ্যা বাস্তব সংখ্যার মধ্যে অন্তর্গত সেই কারণে মূলদ সংখ্যার ধর্মাবলি বাস্তব সংখ্যার ক্ষেত্রেও প্রযোজ্য । এছাড়াও বাস্তব সংখ্যার নিম্নলিখিত কয়েকটি ধর্ম আছে -
1. বাস্তব সংখ্যা দ্বারা যেকোনো দৈর্ঘ্য পরিমাপ করা যায়, অর্থাৎ সংখ্যা অক্ষের উপরে অবস্থিত যেকোনো বিন্দু বাস্তব সংখ্যা দ্বারা প্রকাশ করা যায় ।
2. বাস্তব সংখ্যা সর্বত্র নিবিড় তাদের মধ্যে কোনো ফাঁক নেই । অর্থাৎ দুটি বাস্তব সংখ্যার মধ্যে অসংখ্য বাস্তব সংখ্যা থাকে ।
3. সব বীজগাণিতিক ও অবিজগাণিতিক সংখ্যা বাস্তব সংখ্যা সেটের অন্তর্গত হয় ।
4. কোনো বাস্তব সংখ্যা সেটের প্রকাশ সসীম অথবা আবৃত্ত ও অসীম অথবা অপৌনঃপুনিক ও অসীম হতে পারে । যদি কোনো সংখ্যাকে দশমিকে প্রকাশ করলে যদি সসীম অথবা আবৃত্ত অসীম হয়, তবে বাস্তব সংখ্যাটি মূলদ হবে । তা না হলে তা অমূলদ সংখ্যাকে প্রকাশ করবে ।
কয়েকটি সংজ্ঞা (A Few Definitions)
বাস্তব সংখ্যা সম্মন্ধে আলোচনা করে গিয়ে আমাদের কয়েকটি বিষয় সম্পর্কে জানতে হয়
(১) ধ্রূবক (Constant):- কোনো গাণিতিক অনুসন্ধানে বা বিজ্ঞানের পরীক্ষায় যদি একটি রাশি বা প্রতীকের মানের কোনো পরবর্তন না হয় , তবে ওই রাশি বা প্রতীককে ধ্রূবক (Constant) বলা হয় ।
ধ্রূবক সাধারণত ইংরাজি বর্ণমালা দ্বারা প্রকাশ করা হয় । গণিতে ধ্রূবক দুই ধরণের হয়
(i) স্থির বা নির্দিষ্ট ধ্রূবক (fixed or absolute constant) :- প্রাথমিক শর্তাবলী পরিবর্তিত হলেও যদি কোনো গাণিতিক অনুসন্ধানে একটি রাশি বা প্রতীকের মানের কোনো পরিবর্তন না হয় তবে ওই রাশিকে স্থির বা নির্দিষ্ট ধ্রূবক (fixed or absolute constant) বলে । যেমন কোনো বৃত্তের আকার পরিবর্তিত হলেও পরিধির দৈর্ঘ্য ও ব্যাসার্ধের দৈর্ঘ্যের অনুপাতের কোনো পরিবর্তন হয় না । সুতরাং ওই অনুপাতটি একটি স্থির ধ্রূবক । যে কোনো বাস্তব সংখ্যা একটি স্থির ধ্রূবক ।
(ii) অনির্দিষ্ট ধ্রূবক বা প্যারামিটার (arbitrary constant or parameter) :- কোনো গাণিতিক অনুসন্ধানে একটি প্রদত্ত প্রাথমিক শর্তের ক্ষেত্রে যদি কোনো রাশি বা প্রতীকের মান অপরিবর্তিত থাকে, কিন্তু অনুসন্ধানের প্রাথমিক শর্তাবলী পরিবর্তিত হলে, যদি ওই রাশি বা প্রতীকের মান পরিবর্তিত হয়, তবে ওই রাশি বা প্রতীককে অনির্দিষ্ট ধ্রূবক বা প্যারামিটার (arbitrary constant or parameter) । যেমন মনে করি মূলবিন্দুগামী কোনো সরলরেখা সমীকরণ হল y = mx । এখন যদি মূলবিন্দুগামী সরলরেখা x অক্ষের সাথে [tex]{60^ \circ }[/tex] কোন করে থাকে তাহলে [tex]m = \tan {60^ \circ } = \sqrt 3 [/tex] হবে । আবার ওই মূলবিন্দুগামী সরলরেখা যদি x অক্ষের সাথে [tex]{30^ \circ }[/tex] কোন করে থাকে তবে [tex]m = \tan {30^ \circ } = \frac{1}{{\sqrt 3 }}[/tex] হবে । তাহলে দেখা যাচ্ছে m এর মান বিভিন্ন শর্তের ক্ষেত্রে বিভিন্ন হয় ।
(২) চলরাশি (Variable):- ধরা যাক একটি সসীম বা অসীম সংখ্যক বাস্তব সংখ্যার সেট হল X . এখন এই X সেটের যেকোনো একটি পদ হল x .এই x কে X সেটের সাপেক্ষে একটি চলরাশি বা চল (Variable) বা বাস্তব চলরাশি (Real Variable) বলা হয় ।
সংজ্ঞা থেকে বোঝা যায় x এর মান X সেটের যেকোনো পদের সমান হতে পারে । x এর পক্ষে গ্রহণযোগ্য মান সমূহের সংকলনকে x চলরাশির অঞ্চল বা এলাকা (domain of x) বলা হয় । কোনো চলরাশির কথা বলতে হলে সর্বদাই তার অঞ্চলের কথা উল্লেখ করতে হয় । চলরাশির অঞ্চল থেকে বোঝা যায় অঞ্চলের প্রকৃতি কেমন হবে, অর্থাৎ সন্তত বা অবিচ্ছিন্ন (continuous) এবং অসন্তত বা বিচ্ছিন্ন (discrete) ।
সন্তত বা অবচ্ছিন্ন (continuous) :- যে চলরাশির অঞ্চলে গণনা করা যায় না এই রকম অসীম সংখ্যক বাস্তব মান থাকে , সেই চলরাশিকে সন্তত বা অবিচ্ছিন্নতা (continuous) বলা হয় ।
উদাহরণস্বরূপ মনে করি Y হল একটি বাস্তব সংখ্যার সেট যার মধ্যে y যে কোনো পদ এমন হয় যে , a < x <b . যেখানে a ও b দুটি বাস্তব সংখ্যা অর্থাৎ Y = { y : a < y < b } । আমরা জানি দুটি বাস্তব সংখ্যার মধ্যে অসংখ্য বাস্তব সংখ্যা আছে যা গণনা করা যায় না । সুতরাং y চলরাশির অঞ্চল গণনা করা যায় না এইরকম অসংখ্য বাস্তব মান আছে । তাই y চলরাশিকে সন্তত বা অবিচ্ছিন্ন বলব ।
অসন্তত বা বিচ্ছিন্ন (discrete):- যে চলরাশির অঞ্চলে সসীম সংখ্যক অথবা গণনা করা যায় এমন অসীম সংখ্যক বাস্তব মান থাকে , সেই রকম চলরাশিকে অসন্তত বা বিচ্ছিন্ন (discrete) বলা হয় ।
উদাহরণস্বরূপ মনে করি x চলরাশি দ্বারা একটি ছক্কায় প্রাপ্ত অঙ্ক সূচিত হল , অর্থাৎ যদি x এর অঞ্চল X সেট হয় তাহলে X = { 1 , 2 , 3 , 4 , 5 , 6 } । স্পষ্টতই x এর পক্ষে 1 , 2 , 3 , 4 , 5 ও 6 এই ছয়টি বাস্তব মান গ্রহণ করা সম্ভব যা গণনা করা যায় । তাই x চলরাশির অঞ্চল হবে অসন্তত বা বিচ্ছিন্ন । আবার মনে করি x চলরাশির অঞ্চল হল একটি স্বাভাবিক সংখ্যার সেট। অর্থাৎ N = { x : x একটি স্বাভাবিক সংখ্যা } . এখানে x চলরাশির অঞ্চলে গণনা করা যায় এমন অসীম সংখ্যক বাস্তব মান আছে । সুতরাং x একটি অসন্তত চলরাশি ।
(৩) বিস্তার (Interval):- যদি a ও b দুটি বাস্তব সংখ্যা এবং a < b হয় , তাহলে a ও b এর মধ্যবর্তী সব বাস্তব সংখ্যাসমূহের সংকলনকে a ও b এর বিস্তার বলা হয় ।
মনে করি x , a ও b বিস্তারে অন্তর্গত যেকোনো একটি বাস্তব সংখ্যা । যদি a এবং b বাস্তব সংখ্যা দুটি বিস্তারে অন্তর্গত না হয় তাহলে বিস্তারটি (a , b) প্রতীক দ্বারা প্রকাশ করা হয় । এক্ষত্রে (a , b) বিস্তারকে মুক্ত বিস্তার (Open Interval) বলে । a ও b সংখ্যা দুটি বিস্তারে অন্তর্গত হলে, অর্থাৎ [tex]a \le x \le b[/tex] হলে বিস্তারটিকে [a , b] প্রতীক দ্বারা প্রকাশ করা হয় । এক্ষেত্রে [a , b] বিস্তারকে বদ্ধ বিস্তার (Close Interval) বলে । যদি a সংখ্যাটি বিস্তারে অন্তর্গত এবং b সংখ্যাটি বিস্তারে অন্তর্গত না হয় অর্থাৎ [tex]a \le x < b[/tex] হয় , তবে বিস্তারকে [a ,b) এই প্রতীক দ্বারা প্রকাশ করা হয় । এক্ষেত্রে বিস্তারকে ডানপ্রান্তে মুক্ত বলা হয় । আবার অন্যভাবে a সংখ্যাটি বিস্তারে অন্তর্গত না হয় কিন্তু b সংখ্যাটি বিস্তারে অন্তর্গত হয় অর্থাৎ [tex]a < x \le b[/tex] হয় , তবে বিস্তারকে (a , b] এই প্রতীক দ্বারা প্রকাশ করা হয় । এক্ষেত্রে বিস্তারকে বামপ্রান্তে মুক্ত বলা হয় । [tex]a \le x < b[/tex] ও [tex]a < x \le b[/tex] এই দুটি বিস্তারের একপ্রান্ত মুক্ত এবং একপ্রান্ত বদ্ধ বলে এদেরকে অর্ধমুক্ত বা অর্ধবদ্ধ (half open or half close) বলে ।
(৪) বাস্তব সংখ্যার পরম মান (Absolute value or modulus of real number):- যেকোনো একটি বাস্তব সংখ্যা x এর পরম মান ।x। প্রতীক দ্বারা প্রকাশ করা হয় এবং তার সংজ্ঞা নিম্নরূপে দেওয়া হল
।x। = x ,যখন x > 0
= 0 , যখন x = 0
= -x , যখন x < 0
প্রদত্ত সংজ্ঞা থেকে বোঝাযাচ্ছে ।x। এর মান কখনও ঋণাত্মক হতে পারেনা ।
উদাহরণস্বরূপ x = 2 হলে , ।x। = ।2। = 2
x = 0 , হলে |x| = |0| = 0
x = -2 , হলে |x| = |-2| = -(-2) = 2
সুতরাং কোনো বাস্তব সংখ্যার পরম মান বলতে তার সংখ্যমান ( Numerical value ) বোঝায় ।
পরম মানের বৈশিষ্ট্য (Properties of absolute values)
x , y যেকোনো দুটি বাস্তব সংখ্যা হলে ,
(i) ।x। = ।-x।
উদাহরণস্বরূপ , x = 2 হলে , |x| = |2| = 2 এবং |-x| = |-2| = 2
(ii) [tex]x \le \left| x \right|[/tex] এবং [tex] - x \le \left| x \right|[/tex]
উদাহরণস্বরূপ , x = 2 হলে , |x| = |2| = 2 অতএব x = |x|
x = -2 হলে , |x| = |-2| = 2 অতএব x < |x|
(iii) ।x - y। = ।y - x।
প্রমাণ :- ।x - y। = ।-(y - x)। = ।y - x।
(iv) ।x - y। = ( x - y) , যখন x > y
= -( x - y) , যখন x < y
(v) x = y হলে , ।x - y। = 0 হবে ; বিপরীতক্রমে , ।x - y। = 0 হলে , x = y হবে ।
(vi) [tex]\left| {x + y} \right| \le \left| x \right| + \left| y \right|[/tex]
প্রমাণ :- স্পষ্টতই , [tex]x \le \left| x \right|[/tex] ; [tex] - x \le \left| x \right|[/tex] ; এবং [tex]y \le \left| y \right|[/tex] ; [tex] - y \le \left| y \right|[/tex]
এখন , [tex]x + y \ge 0[/tex] হলে ,
[tex]\left| {x + y} \right| = x + y \le \left| x \right| + \left| y \right|...........(1)[/tex]
আবার , x + y < 0 হলে ,
[tex]\left| {x + y} \right| = - \left( {x + y} \right) = - x + \left( { - y} \right) \le \left| x \right| + \left| y \right|..........(2)[/tex]
সুতরাং (1) ও (2) থেকে পাই , [tex]\left| {x + y} \right| \le \left| x \right| + \left| y \right|[/tex]
(vii) [tex]\left| {x - y} \right| \le \left| x \right| + \left| y \right|[/tex]
প্রমাণ :- [tex]\left| {x - y} \right| = \left| {x + \left( { - y} \right)} \right| \le \left| x \right| + \left| { - y} \right|[/tex] (iv) থেকে পাই ।
বা , [tex]\left| {x - y} \right| \le \left| x \right| + \left| y \right|[/tex]
(viii) [tex]\left| {a \pm b} \right| \le \left| {\left| a \right| - \left| b \right|} \right|[/tex]
প্রমাণ :- স্পষ্টতই , [tex]\left| a \right| \ge \left| b \right|[/tex] হলে ,
[tex]\begin{array}{l}
\left| a \right| = \left| {\left( {a + b} \right) - b} \right| \le \left| {a + b} \right| + \left| b \right|\\
\Rightarrow \left| {a + b} \right| \ge \left| a \right| - \left| b \right|.......(1)
\end{array}[/tex]
আবার , [tex]\left| b \right| \ge \left| a \right|[/tex] হলে ,
[tex]\begin{array}{l}
\left| b \right| = \left| {\left( {a + b} \right) - a} \right| \le \left| {a + b} \right| + \left| a \right|\\
\Rightarrow \left| {a + b} \right| \ge \left| b \right| - \left| a \right|..........(2)
\end{array}[/tex]
সুতরাং (1) ও (2) থেকে পাই
[tex]\left| {a + b} \right| \ge \left| {\left| a \right| - \left| b \right|} \right|[/tex]
একইভাবে [tex]\left| a \right| \ge \left| b \right|[/tex] হলে ,
[tex]\begin{array}{l}
\left| a \right| = \left| {\left( {a - b} \right) + b} \right| \le \left| {a - b} \right| + \left| b \right|\\
\Rightarrow \left| {a - b} \right| \ge \left| a \right| - \left| b \right|.......(3)
\end{array}[/tex]
আবার , [tex]\left| b \right| \ge \left| a \right|[/tex] হলে ,
[tex]\begin{array}{l}
\left| b \right| = \left| {\left( {b - a} \right) + a} \right| \le \left| {b - a} \right| + \left| a \right|\\
\Rightarrow \left| {b - a} \right| \ge \left| b \right| - \left| a \right|..........(4)
\end{array}[/tex]
সুতরাং (3) ও (4) থেকে পাই ,
[tex]\left| {a - b} \right| \ge \left| {\left| a \right| - \left| b \right|} \right|[/tex]
(ix) [tex]\left| {xy} \right| = \left| x \right|\left| y \right|[/tex]
প্রমাণ :-
প্রথমত , মনে করি [tex]x \ge 0,y \ge 0[/tex] অতএব [tex]xy \ge 0[/tex]
এখন সংজ্ঞা থেকে পাই ।x। = x , ।y। = y এবং ।xy। = xy
অতএব ।xy। = ।x।।y।
দ্বিতীয়ত , [tex]x \ge 0,y < 0[/tex] হলে , [tex]xy \le 0[/tex]
সুতরাং সংজ্ঞা থেকে পাই ।x। = x , ।y। = - y এবং ।xy। = - xy
অতএব ।xy। = - xy = x .(-y) = ।x।।y।
একইভাবে [tex]x < 0,y \ge 0[/tex] হলে , আমরা প্রমাণ করতে পারি ।xy। = ।x।।y।.
সুতরাং x এবং y এর সব বাস্তব মানে ।xy। = ।x।।y।.
(x) [tex]\left| {\frac{x}{y}} \right| = \frac{{\left| x \right|}}{{\left| y \right|}}\left( {y \ne 0} \right)[/tex]
প্রমাণ :-
[tex]\begin{array}{l}
\left| {\frac{x}{y}} \right|\\
= \left| {x \cdot \frac{1}{y}} \right|\\
= \left| x \right| \cdot \left| {\frac{1}{y}} \right|\\
= \left| x \right| \cdot \frac{1}{{\left| y \right|}}\\
= \frac{{\left| x \right|}}{{\left| y \right|}}
\end{array}[/tex]
(xi) [tex]\left| x \right| \le y[/tex] হলে , [tex] - y \le x \le y[/tex] হবে ।
প্রমাণ :- মনে করি [tex]x \ge 0[/tex] তাহলে ।x। = x এবং [tex] - x \le x[/tex]
এখন [tex]\left| x \right| \le y[/tex] হওয়ায় , [tex]x \le y \Rightarrow - x \ge - y[/tex]
সুতরাং [tex] - y \le - x \le x \le y \Rightarrow - y \le x \le y[/tex]
আবার [tex]x \le 0[/tex] হলে ।x। = -x এবং [tex] - x \ge x[/tex]
এখন [tex]\left| x \right| \le y[/tex] হওয়ায় , [tex] - x \le y \Rightarrow x \ge - y[/tex]
সুতরাং [tex] - y \le x \le - x \le y \Rightarrow - y \le x \le y[/tex]
(xii) [tex]\left| x \right| \ge y[/tex] হলে [tex]x \ge y[/tex] অথবা [tex]x \le - y[/tex] হবে ।
প্রমাণ :- যদি [tex]x \ge 0[/tex] হয় তবে ।x। = x
তাহলে [tex]\left| x \right| \ge y \Rightarrow x \ge y[/tex]
আবার [tex]x \le 0[/tex] হয় , তবে ।x। = -x
তাহলে
[tex]\begin{array}{l}
\left| x \right| \ge y\\
\Rightarrow - x \ge y\\
\Rightarrow x \le - y
\end{array}[/tex]
(xiii) [tex]0 < \left| {x - a} \right| \le \delta [/tex] হলে [tex]a - \delta \le x \le a + \delta [/tex] হবে , যেখানে [tex]x \ne a[/tex]
প্রমাণ :- [tex]0 < \left| {x - a} \right|[/tex] থেকে বোঝাযায় , [tex]x \ne a[/tex]
আবার [tex]\left| {x - a} \right| \le \delta [/tex] থেকে পাই , [tex] - \delta \le x - a \le \delta [/tex] (xi) বৈশিষ্ট্য থেকে পাই।
[tex]\begin{array}{l}
- \delta \le x - a \le \delta \\
\Rightarrow a - \delta \le x - a + a \le a + \delta \\
\Rightarrow a - \delta \le x \le a + \delta
\end{array}[/tex]
(xiv) [tex]\left| {x - a} \right| \ge \delta [/tex] হলে , [tex]x \ge a + \delta [/tex] অথবা [tex]x \le a - \delta [/tex] হবে ।
(xv) [tex]\left| {x - a} \right| = b[/tex] হলে , [tex]x = a + b[/tex] অথবা [tex]x = a - b[/tex] হবে ।
সংক্ষিপ্তকরণ (Summarisation)
(1) 1 , 2 , 3 , 4 ,............ সংখ্যসমূহকে স্বাভাবিক সংখ্যা বলা হয়। স্বাভাবিক সংখ্যার সেটকে N দ্বারা সূচিত করা হয় ; অর্থাৎ
N = { 1 , 2 , 3 , 4 , .......... }
(2) স্বাভাবিক সংখ্যসমূহের সঙ্গে - 1 , - 2 , - 3 , .......... এবং 0 (শূন্য) সংখ্যসমূহের সংযোজন করে যেসব সংখ্যা পাওয়া যায় তাদের পূর্ণসংখ্যা বা অখন্ড সংখ্যা বলে । পূর্ণসংখ্যার সেটকে I দ্বারা সূচিত করা হয় ।; অর্থাৎ
[tex]I = \left\{ {0, \pm 1, \pm 2, \pm 3,..........} \right\}[/tex]
(3) p ও q পরস্পর মৌলিক দুটি পূর্ণ হলে , [tex]\frac{p}{q}[/tex] আকারে প্রকাশিত সংখ্যাকে মূলদ সংখ্যা বলা হয় । এখানে q \[\left( { \ne 0} \right)\] কে ধনাত্মক পূর্ণসংখ্যা এবং p কে ধনাত্মক বা ঋণাত্মক পূর্ণসংখ্যা বা শূন্য ধরা হয় । মূলদ সংখ্যার সেটকে Q দ্বারা সূচিত করা হয় । অর্থাৎ [tex]Q = \left\{ {\frac{p}{q}:p \in I,q \in N} \right\}[/tex]
(4) শূন্য দ্বারা ভাগ অসংজ্ঞাত ; অর্থাৎ [tex]\frac{a}{0}[/tex] এর কোনো অর্থ নেই ।
(5) যেকোনো মূলদ সংখ্যাকে সসীম দশমিকে নাহলে আবৃত্ত দশমিকে প্রকাশ করা যায় এবং বিপরীতক্রমে তাও সত্য ।
(6) প্রত্যেক মূলদ সংখ্যাকে সংখ্যা - অক্ষের উপরে অবস্থিত একটি নির্দিষ্ট বিন্দু দ্বারা প্রকাশ করা যায় , কিন্তু এটি বিপরীতক্রমে সত্য নয় অর্থাৎ সংখ্যা অক্ষের উপরে অবস্থিত প্রত্যেক বিন্দু দ্বারা মূলদ সংখ্যা প্রকাশিত নাও হতে পারে ।
(7) যে সংখ্যাকে [tex]\frac{p}{q}[/tex] আকারে প্রকাশ করা যায়না অথবা যে সংখ্যার দশমিক আকার অপৌনঃপুনিক ও অসীম তাকে অমূলদ সংখ্যা বলে ।
(8) সমস্ত মূলদ বা অমূলদ সংখ্যার সংকলন বা সমষ্টিকে বাস্তব সংখ্যা বলে। বাস্তব সংখ্যার সেটকে R দ্বারা সূচিত করা হয় ; অর্থাৎ
R = { x : x একটি মূলদ সংখ্যা বা অমূলদ সংখ্যা }
(9) সংখ্যা অক্ষের উপরে অবস্থিত এক একটি বিন্দু এক একটি বাস্তব সংখ্যাকে প্রকাশ করে ।
(10) বাস্তব সংখ্যা সর্বত্র নিবিড় এবং তাদের মধ্যে কোনো ফাঁক নেই ।
(11) মনে করি a ও b ( >a ) দুটি বাস্তব সংখ্যা এবং x তাদের মধ্যবর্তী যেকোনো একটি বাস্তব সংখ্যা। তাহলে (a , b) বা a < x < b কে a ও b সংখ্যা দুটির মুক্ত বিস্তার এবং [a , b] বা [tex]a \le x \le b[/tex] কে তাদের বদ্ধ বিস্তার বলে ।
(12) যেকোনো বাস্তব সংখ্যা x এর পরম মান ।x। প্রতীক দ্বারা প্রকাশ করা হয় ।
।x। = x ,যখন x > 0
= 0 , যখন x = 0
= -x , যখন x < 0
উদাহরণ 1. প্রমাণ করো যে [tex]\sqrt 3 [/tex] মূলদ সংখ্যা নয় ।
সমাধান :- ধরি [tex]\sqrt 3 [/tex] হল একটি মূলদ সংখ্যা। অতএব সংজ্ঞা অনুযায়ী আমরা লিখতে পারি [tex]\frac{p}{q} = \sqrt 3 [/tex] . যেখানে p হল একটি পূর্ণসংখ্যা বা অখন্ড সংখ্যা এবং q হল স্বাভাবিক সংখ্যা ।
তাহলে
[tex]\begin{array}{l}
{\left( {\frac{p}{q}} \right)^2} = 3\\
\Rightarrow \frac{{{p^2}}}{q} = 3q
\end{array}[/tex]
আমরা জানি যে p ও q পরস্পর মৌলিক । অতএব [tex]{{p^2}}[/tex] এবং q পরস্পর মৌলিক পূর্ণসংখ্যা হবে । সুতরাং [tex]\frac{{{p^2}}}{q}[/tex] দ্বারা একটি মূলদ সংখ্যা প্রকাশিত হচ্ছে যা কোনো ধনাত্মক পূর্ণসংখ্যা নয় । অপর দিকে 3q দ্বারা একটি স্বাভাবিক সংখ্যা প্রকাশিত হচ্ছে । সুতরাং আমাদের কল্পনা সত্য নয় । অর্থাৎ [tex]\sqrt 3 [/tex] একটি মূলদ সংখ্যা হতে পারে না ।
উদাহরণ 2. দেখাও যে বিজোড় স্বাভাবিক সংখ্যার বর্গকে 8 দ্বারা ভাগ করলে ভাগশেষ সর্বদা 1 হবে ।
সমাধান :- মনে করি একটি বিজোড় স্বাভাবিক সংখ্যা হল ( 2n + 1) যেখানে n হল যেকোনো স্বাভাবিক সংখ্যা . এখন এই বিজোড় স্বাভাবিক সংখ্যার বর্গকে 8 দ্বারা ভাগ করলে আমরা পাই
[tex]\begin{array}{l}
\frac{{{{\left( {2n + 1} \right)}^2}}}{8}\\
= \frac{{4{n^2} + 4n + 1}}{8}\\
= \frac{{4n\left( {n + 1} \right) + 1}}{8}...........(i)
\end{array}[/tex]
আমরা জানি পরপর যেকোনো দুটি স্বাভাবিক সংখ্যার গুণফল একটি জোড় সংখ্যা হবে । অতএব আমরা মনে করতে পারি n(n +1) = 2m . (i) নং সমীকরণে এই মান বসিয়ে পাই [tex]\frac{{4 \times 2m + 1}}{8} = \frac{{8m + 1}}{8}[/tex] . ( 8m + 1 ) কে 8 দ্বারা ভাগ করলে ভাগশেষ সর্বদা 1 হবে ।
- 19879 views
