The Routh-Hurwitz criterion gives the information about the absolute stability, not the relative stability of a system. It is unwise to determine all the roots of the system, which becomes more complex especially for higher order system to find its stability. For stability, all the roots must be in the negative half of s-plane.
Using the Rougth-Hurwitz method, the stability information can be obtained without need to solve the closed loop system poles. This can be achieved by determining the number of poles that are in left-half or right-half plane and on the imaginary axis.
The procedure of Routh-Hurwitz stability criterion as follows:
- The polynomial equation in 's' is written in descending order : [tex]{a_0}{s^n} + {a_1}{s^{n - 1}} + ...... + {a_{n - 1}}s + {a_n} = 0[/tex] Where coefficients are real quantities. We assume that [tex]{a_n} \ne 0[/tex], i.e. the possibility of having any zero root has been removed.
- If any of the coefficients is zero or negative in the presence of at least one positive coefficient, there is a root or roots which are imaginary or which have positive real parts. Therefore in such a case, the system is not stable. If one is interested only in absolute stability, there is no need to follow the procedure further. If all the coefficients of characteristic equation are negative they can be made positive by multiplying both side of the equation by -1.
If all the coefficients are positive, arrange the coefficients of the polynomial in rows and columns according to the following pattern,
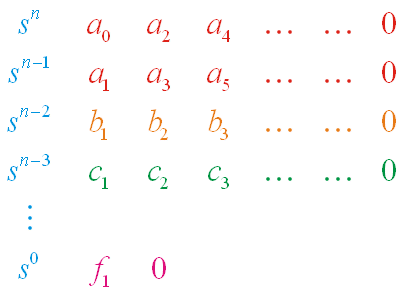
consisting of (n+1) rows, the first two being formed from the given polynomial. The b,c entries are determined by the algorithm illustrated as follows: [tex]{b_1} = \frac{{{a_1}{a_2} - {a_0}{a_3}}}{{{a_1}}}[/tex]
[tex]{b_2} = \frac{{{a_1}{a_4} - {a_0}{a_5}}}{{{a_1}}}[/tex]
The evaluation of the b's is continued until the remaining ones are all zero. The pattern of cross-multiplying the coefficients of the two previous rows is followed in evaluating the c's .
[tex]{c_1} = \frac{{{b_1}{a_3} - {a_1}{b_2}}}{{{b_1}}}[/tex]
[tex]{c_2} = \frac{{{b_1}{a_5} - {a_1}{b_3}}}{{{b_1}}}[/tex]
This process is continued until the (n+1)th row has been completed. The complete Routh-Hurwitz array of coefficients is triangular.
The Routh-Hurwitz stability criterion states that the number of roots of F(s)=0 with positive real parts is equal to the number of changes in sign of the coefficients of the first column of the array.
The necessary and sufficient condition that all roots of F(s) lie in the left half of s-plane is that all the coefficients of F(s)=0 be present and of the same sign and all terms in the first column of the array have same signs.
- 677 views






