পূরক কোণের ত্রিকোণমিতিক অনুপাত

পূরক কোণের ত্রিকোণমিতিক অনুপাত ( Trigonometrical Ratios of Complementary Angles )

পূরক কোণ ( Complementary Angles )

  জ্যামিতিতে আমরা দেখেছে যখন দুটি কোণের মানের সমষ্টি [tex]{90^ \circ }[/tex] হয় তখন কোণ দুটির একটিকে অপরটির পূরক কোণ ( Complementary Angles ) বলে। যেমন , [tex]{60^ \circ } + {30^ \circ } = {90^ \circ }[/tex] , সুতরাং [tex]{60^ \circ }[/tex] কোণের পূরক কোণ [tex]{30^ \circ }[/tex] এবং [tex]{30^ \circ }[/tex] কোণের পূরক কোণ হবে [tex]{60^ \circ }[/tex] . বিষয়টি আরো সাধারণভাবে বললে তা দাঁড়ায় একটি কোণের মান যদি [tex]\theta [/tex] হয় , তবে তার পূরক কোণের মান হবে [tex]{90^ \circ } - \theta [/tex] .

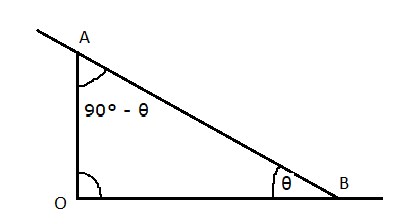
এখন আমাদের দেখতে হবে [tex]\theta [/tex] কোণের  ত্রিকোণমিতিক অনুপাত যদি জানা থাকে , তবে তার থেকে কী করে [tex]{90^ \circ } - \theta [/tex] কোণের ত্রিকোণমিতিক অনুপাত নির্ণয় করা যায়। 

উপরের চিত্রে [tex]\angle ABO = \theta [/tex] এবং [tex]\angle OAB = {90^ \circ } - \theta [/tex] . অতএব এদের একটি কোন অপরটির পূরক। এবার দেখা যাক এই দুটি সূক্ষকোণের পরিপ্রেক্ষিতে কোনটি অতিভুজ , কোনটি লম্ব এবং কোনটি ভূমি। 

[tex]\theta [/tex] কোণের পরিপ্রেক্ষিতে 

AB হল অতিভুজ ,

OA হল লম্ব 

এবং OB হল ভূমি 

[tex]{90^ \circ } - \theta [/tex] কোণের পরিপ্রেক্ষিতে 

AB হল অতিভুজ ,

OB হল লম্ব 

এবং OA হল ভূমি 

এখন [tex]{90^ \circ } - \theta [/tex] কোণের ক্ষেত্রে 

[tex]\begin{array}{l}
\sin \left( {{{90}^ \circ } - \theta } \right) = \frac{{OB}}{{AB}}\\
\cos ec\left( {{{90}^ \circ } - \theta } \right) = \frac{{AB}}{{OB}}\\
\cos \left( {{{90}^ \circ } - \theta } \right) = \frac{{OA}}{{AB}}\\
\sec \left( {{{90}^ \circ } - \theta } \right) = \frac{{AB}}{{OA}}\\
\tan \left( {{{90}^ \circ } - \theta } \right) = \frac{{OB}}{{OA}}\\
\cot \left( {{{90}^ \circ } - \theta } \right) = \frac{{OA}}{{OB}}
\end{array}[/tex]

কিন্তু [tex]\theta [/tex] কোণের ক্ষেত্রে 

[tex]\begin{array}{l}
\sin \theta  = \frac{{OA}}{{AB}}\\
\cos ec\theta  = \frac{{AB}}{{OA}}\\
\cos \theta  = \frac{{OB}}{{AB}}\\
\sec \theta  = \frac{{AB}}{{OB}}\\
\tan \theta  = \frac{{OA}}{{OB}}\\
\cot \theta  = \frac{{OB}}{{OC}}
\end{array}[/tex]

উপরের আলোচনা থেকে দেখতে পাওয়া যায় যে 

[tex]\begin{array}{l}
\sin \left( {{{90}^ \circ } - \theta } \right) = \cos \theta \\
\cos \left( {{{90}^ \circ } - \theta } \right) = \sin \theta \\
\cos ec\left( {{{90}^ \circ } - \theta } \right) = \sec \theta \\
\sec \left( {{{90}^ \circ } - \theta } \right) = \cos ec\theta \\
\tan \left( {{{90}^ \circ } - \theta } \right) = \cot \theta \\
\cot \left( {{{90}^ \circ } - \theta } \right) = \tan \theta 
\end{array}[/tex]