বাস্তব সমস্যায় ত্রিকোণমিতিক অনুপাতের প্রয়োগ
সূচনা ( Introduction )
সূচনাতে ত্রিকোণমিতি কেন বলতে গিয়ে আমরা বলেছিলাম যে সঠিকভাবে মেপে বা গণিতের অন্য কোনো শাখার সাহায্যে কোনো কিছুর উচ্চতা বা দৈর্ঘ্য ও দূরত্ব সম্মন্ধে অনেক তথ্য , যা আমরা সহজে নির্ণয় করতে পারিনা , তা ত্রিকোণমিতির সাহায্যে সহজেই নির্ণয় করা যায়।
মনে করি মাঠের মাঝখানে একটি উঁচু খাড়াই পাহাড় রয়েছে , এর উচ্চতা আমাদের নির্ণয় করতে হবে। খাড়াই পাহাড়ে ওঠা আমাদের পক্ষে কষ্টসাধ্য , এমনকি বিপদসংকুল হতে পারে। ত্রিকোণমিতির সাহায্যে আমরা পাহাড়ে ওঠার কষ্ট ও ঝুঁকি না নিয়েও মাঠের মাটিতে দাঁড়িয়েই পাহাড়ের উচ্চতা নির্ণয় করতে পারি। তেমনি খাল পার না হয়েও খালের ওপারে তাল গাছের উচ্চতা ও দূরত্ব নির্ণয় করতে পারি। কোনো গাছ বা মনুমেন্টের ছায়ার দৈর্ঘ্য মেপে তার উচ্চতা নির্ণয় করতে পারি। তার চেয়েও বড়ো কথা পৃথিবীর মাটিতে দাঁড়িয়ে বলে দিতে পারি চন্দ্র , সূর্যের ব্যাস কত , তারা কত দূরে আছে ইত্যাদি অনেক কিছু। কী করে তা নির্ণয় করা যায় তা এই অধ্যায়ে উদাহরণসহ দেখানো হল।
উন্নতি কোণ ও অবনতি কোণ সম্বন্ধে ধারণা ( Concept of Angle of Elevation and Angle of Depression )
মনে করি AB একটি স্তম্ভ যার শীর্ষবিন্দু A এবং স্তম্ভের পাদদেশের সঙ্গে অনুভূমিক সরলরেখাটি হল BP .
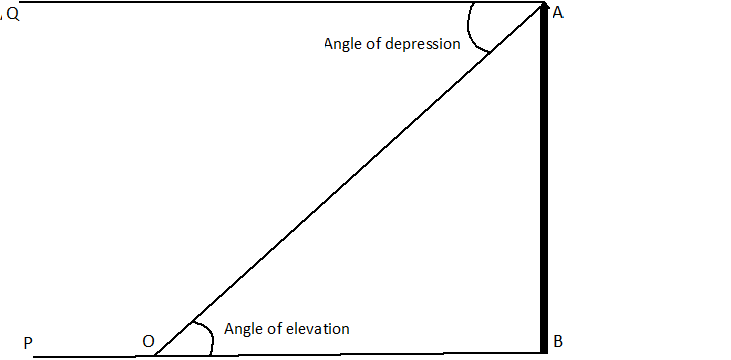
এবার মনে করি BP এর উপর O যেকোনো একটি বিন্দু। এখন একজন দর্শক O বিন্দুতে চোখ রেখে চূড়ার দিকে তাকালে যে কোণে স্তম্ভের চূড়াটি দেখতে পাবে তা হল ∠BOA . এই কোণটিকে বলা হয় উন্নতি কোণ ( Angle of Elevation ) . সুতরাং এখানে O বিন্দুর সাপেক্ষে A বিন্দুর উন্নতি কোণ ∠BOA .
আবার এমন হতে পারে যে , স্তম্ভের চূড়ায় উঠে কোনো কোনো এক ব্যক্তি A বিন্দুতে চোখ রেখে স্তম্ভের পদবিন্দুগামী অনুভূমিক রেখার উপর O বিন্দুতে একটি বস্তু দেখেছেন। তখন সেই ব্যক্তি যে কোণে O বিন্দুতে বস্তুটি দেখবেন সেই কোণটি হল A বিন্দু সাপেক্ষে O বিন্দুর অবনতি কোণ ( Angle of Depression ) . এই অবনতি কোণের পরিমাপ জানতে হলে A বিন্দু দিয়ে অঙ্কিত অনুভূমিক সরলরেখা AQ কল্পনা করতে হবে এবং তখন অবনতি কোণের পরিমাপ হবে ∠QAO .
লক্ষ্য রাখতে হবে এখানে BO ।। AQ এবং AO তাদের ভেদক।
তাই উন্নতি কোণ ∠BOA = অবনতি কোণ ∠QAO ( একান্তর কোণ বলে ) .
কিন্তু তবু এদের আলাদা আলাদা ভাবে চিহ্নিত করা দরকার কারণ বাস্তব ক্ষেত্রে আমাদের এদের আলাদা আলাদাভাবে নিয়ে সমস্যা সমাধান করতে হবে।
- সমকোণী ত্রিভুজ , উন্নতি কোণ ও অবনতি কোণের প্রয়োগ ও দৈনন্দিন জীবনের বিভিন্ন সমস্যার ত্রিকোণমিতিক সমাধান ।
- 5616 views