জটিল রাশির ধর্ম ( Properties of Complex Numbers)

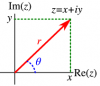
জটিল রাশির কয়েকটি ধর্ম (A Few Properties of Complex Numbers)

(1) x , y বাস্তব এবং x + iy = 0 হলে x = 0 এবং y = 0 হবে । 

প্রমাণ :- x + iy = 0 = 0 + i0

জটিল রাশির সমতা থেকে পাই x = 0 , y = 0 .

(2) x , y , p , q বাস্তব এবং x + iy = p + iq হলে x = p এবং y = q হবে । 

প্রমাণ :- 

$\begin{array}{l} x + iy = p + iq\\  \Rightarrow \left( {x - p} \right) = i\left( {q - y} \right) \end{array}$

উভয়দিকে বর্গ করে পাই 

$\begin{array}{l}  \Rightarrow {\left( {x - p} \right)^2} = {\left\{ {i\left( {q - y} \right)} \right\}^2}\\  \Rightarrow {\left( {x - p} \right)^2} = {i^2}{\left( {q - y} \right)^2}\\  \Rightarrow {\left( {x - p} \right)^2} =  - {\left( {q - y} \right)^2}\\  \Rightarrow {\left( {x - p} \right)^2} + {\left( {q - y} \right)^2} = 0...........\left( i \right) \end{array}$

x , y , p , q বাস্তব তাই ${\left( {x - p} \right)^2}$ এবং ${\left( {q - y} \right)^2}$ এর মান কখনও ঋণাত্মক হতে পারেনা। অতএব (i) নং সমীকরণ সিদ্ধ হবে যখন 

$\begin{array}{l} {\left( {x - p} \right)^2} + {\left( {q - y} \right)^2} = 0\\  \Rightarrow {\left( {x - p} \right)^2} = 0,{\left( {q - y} \right)^2} = 0 \end{array}$

$\begin{array}{l} {\left( {x - p} \right)^2} = 0\\  \Rightarrow x - p = 0\\  \Rightarrow x = p \end{array}$

$\begin{array}{l} {\left( {q - y} \right)^2} = 0\\  \Rightarrow q - y = 0\\  \Rightarrow q = y \end{array}$

(3) বাস্তব সংখ্যার ন্যায় জটিল রাশি যোগ ও গুণ সাপেক্ষে বিনিময় (Commutative), সংযোগ (Associative) এবং বিচ্ছেদ (Distributive) নিয়ম মেনে চলে । 

যদি ${z_1},{z_2},{z_3}$ তিনটি জটিল রাশি হয় তাহলে 

1. ${z_1} + {z_2} = {z_2} + {z_1};{z_1}{z_2} = {z_2}{z_1}$ [ বিনিময় নিয়ম ]

2. $\left( {{z_1} + {z_2}} \right) + {z_3} = {z_1} + \left( {{z_2} + {z_3}} \right);\left( {{z_1} \cdot {z_2}} \right) \cdot {z_3} = {z_1} \cdot \left( {{z_2} \cdot {z_3}} \right)$ [ সংযোগ নিয়ম ]

3. ${z_1}\left( {{z_2} + {z_3}} \right) = {z_1}{z_2} + {z_1}{z_3}$ [ বিচ্ছেদ নিয়ম ]

(4) দুটি পরস্পর অনুবন্দি জটিল রাশির যোগফল ও গুণফল উভয়ই বিশুদ্ধ বাস্তব রাশি । 

প্রমাণ :- মনে করি z = x + iy একটি জটিল রাশি। যেখানে x ও y বাস্তব । 

অতএব এর অনুবন্দি জটিল রাশি হবে $\overline z  = x - iy$

এখন ওদের যোগফল হল 

$\begin{array}{l} z + \overline z \\  = \left( {x + iy} \right) + \left( {x - iy} \right)\\  = 2x \end{array}$

যা একটি বাস্তব রাশি । 

আবার ওদের গুণফল হল 

$\begin{array}{l} z \cdot \overline z \\  = \left( {x + iy} \right) \cdot \left( {x - iy} \right)\\  = {x^2} - ixy + ixy - {\left( {iy} \right)^2}\\  = {x^2} - \left( { - 1} \right){y^2}\\  = {x^2} + {y^2} \end{array}$

যা একটি বাস্তব রাশি । 

(5) দুটি জটিল রাশির যোগফল ও গুণফল উভয়ই বাস্তব হলে জটিল রাশি দুটি অনুবন্দি হবেই । 

প্রমাণ :- মনে করি ${z_1} = {x_1} + i{y_1}$ এবং ${z_2} = {x_2} + i{y_2}$ দুটি জটিল রাশি। যেখানে ${x_1},{y_1},{x_2},{y_2}$ হল বাস্তব এবং উহাদের যোগফল ও গুণফল উভয়ই বাস্তব । 

এখন 

${z_1} + {z_2} = \left( {{x_1} + i{y_1}} \right) + \left( {{x_2} + i{y_2}} \right) = \left( {{x_1} + {x_2}} \right) + i\left( {{y_1} + {y_2}} \right).......\left( i \right)$

${z_1} \cdot {z_2} = \left( {{x_1} + i{y_1}} \right) \cdot \left( {{x_2} + i{y_2}} \right) = \left( {{x_1}{x_2} - {y_1}{y_2}} \right) + i\left( {{x_2}{y_1} + {x_1}{y_2}} \right)........\left( {ii} \right)$

প্রশ্নানুযায়ী (i) এবং (ii) হল বিশুদ্ধ বাস্তব। সুতরাং 

${y_1} + {y_2} = 0$ ..........(iii)

এবং 

${x_2}{y_1} + {x_1}{y_2} = 0$ ........(iv)

সমীকরণ (iii) এবং (iv) থেকে পাই 

$\begin{array}{l} {y_1} + {y_2} = 0\\  \Rightarrow {y_1} =  - {y_2}.......(v) \end{array}$

(v) এবং (iv) থেকে পাই 

$\begin{array}{l} {x_2}{y_1} + {x_1}{y_2} = 0\\  \Rightarrow {x_2}\left( { - {y_2}} \right) + {x_1}{y_2} = 0\\  \Rightarrow {x_1} - {x_2} = 0\\ \left[ {{y_2} \ne 0} \right]\\  \Rightarrow {x_1} = {x_2} \end{array}$

সুতরাং 

${z_1} = {x_1} + i{y_1} = {x_2} - i{y_2} = \overline {{z_2}}$

অর্থাৎ ${z_1},{z_2}$ পরস্পরের অনুবন্দি। 

(6) ${z_1},{z_2}$ দুটি জটিল রাশি হলে $\left| {{z_1} + {z_2}} \right| \le \left| {{z_1}} \right| + \left| {{z_2}} \right|$

প্রমাণ :- মনে করি 

$\begin{array}{l} {z_1} = {r_1}\left( {\cos {\theta _1} + i\sin {\theta _1}} \right)\\ {z_2} = {r_2}\left( {\cos {\theta _2} + i\sin {\theta _2}} \right) \end{array}$

অতএব $\left| {{z_1}} \right| = {r_1}$ এবং $\left| {{z_2}} \right| = {r_2}$

আবার 

$\begin{array}{l} {z_1} + {z_2}\\  = {r_1}\left( {\cos {\theta _1} + i\sin {\theta _1}} \right) + {r_2}\left( {\cos {\theta _2} + i\sin {\theta _2}} \right)\\  = \left( {{r_1}\cos {\theta _1} + {r_2}\cos {\theta _2}} \right) + i\left( {{r_1}\sin {\theta _1} + {r_2}\sin {\theta _2}} \right) \end{array}$

অতএব 

$\begin{array}{l} \left| {{z_1} + {z_2}} \right|\\  = \left| {\left( {{r_1}\cos {\theta _1} + {r_2}\cos {\theta _2}} \right) + i\left( {{r_1}\sin {\theta _1} + {r_2}\sin {\theta _2}} \right)} \right|\\  = \sqrt {{{\left( {{r_1}\cos {\theta _1} + {r_2}\cos {\theta _2}} \right)}^2} + {{\left( {{r_1}\sin {\theta _1} + {r_2}\sin {\theta _2}} \right)}^2}} \\  = \sqrt {{r_1}^2{{\cos }^2}{\theta _1} + {r_2}^2{{\cos }^2}{\theta _2} + {r_1}^2{{\sin }^2}{\theta _1} + {r_2}^2{{\sin }^2}{\theta _2} + 2{r_1}{r_2}\left( {\cos {\theta _1}\cos {\theta _2} + \sin {\theta _1}\sin {\theta _2}} \right)} \\  = \sqrt {{r_1}^2\left( {{{\cos }^2}{\theta _1} + {{\sin }^2}{\theta _1}} \right) + {r_2}^2\left( {{{\cos }^2}{\theta _2} + {{\sin }^2}{\theta _2}} \right) + 2{r_1}{r_2}\cos \left( {{\theta _1} - {\theta _2}} \right)} \\  = \sqrt {{r_1}^2 + {r_2}^2 + 2{r_1}{r_2}\cos \left( {{\theta _1} - {\theta _2}} \right)}  \end{array}$

এখন $\left| {\cos \left( {{\theta _1} - {\theta _2}} \right)} \right| \le 1$

অতএব 

$\begin{array}{l} \left| {{z_1} + {z_2}} \right| \le \sqrt {{r_1}^2 + {r_2}^2 + 2{r_1}{r_2}} \\  \Rightarrow \left| {{z_1} + {z_2}} \right| \le {r_1} + {r_2}\\  \Rightarrow \left| {{z_1} + {z_2}} \right| \le \left| {{z_1}} \right| + \left| {{z_2}} \right| \end{array}$

[ যেকোনো n সংখ্যক জটিল রাশির ক্ষেত্রে এটি প্রযোজ্য হবে , অর্থাৎ 

$\left| {{z_1} + {z_2} + {z_3} + ...... + {z_n}} \right| \le \left| {{z_1}} \right| + \left| {{z_2}} \right| + \left| {{z_3}} \right| + ........ + \left| {{z_n}} \right|$]