সাধারণ তুলা যন্ত্র (Common Balance)
সাধারণ তুলাযন্ত্রের সাহায্যে কোনো বস্তুর ভর পরিমাপ করা হয় । মুদির দোকানে পণ্য-সামগ্রী মাপার জন্য যে দাঁড়িপাল্লা ব্যবহার করা হয়ে থাকে সেগুলিই সাধারণ তুলাযন্ত্রের উদাহরণ । বর্তমানে অবশ্য ইলেক্ট্রনিক মাপ যন্ত্রের ব্যবহার ক্রমশঃ বৃদ্ধি হচ্ছে ।
সাধারণ তুলা যন্ত্রের ভর পরিমাপের নীতি : তুলাযন্ত্রকে নির্ভুল করে বাম দিকের তুলাপাত্রে পরিমেয় বস্তু এবং ডানদিকের তুলাপাত্রে প্রয়োজনীয় 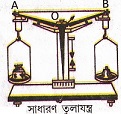 বাটখারা রাখা হয় । AB তুলাদণ্ডের A ও B বিন্দুতে বস্তু ও বাটখারার ওজন ক্রিয়াশীল, আর O হল তুলাদণ্ডের আলম্ব । তুলাদণ্ড অনুভূমিক হলে বলবিদ্যার সূত্রানুসারে বস্তুর ওজন x AO = বাটখারার ওজন x BO । যেহেতু AO = BO, এতএব বস্তুর ওজন = বাটখারার ওজন । অর্থাৎ, বস্তুর ভর = বাটখারার ভর । বাটখারার ওপর লেখা ওজন সংখ্যা পাঠ করে বস্তুর ওজন প্রকাশ করা হয় ।
বাটখারা রাখা হয় । AB তুলাদণ্ডের A ও B বিন্দুতে বস্তু ও বাটখারার ওজন ক্রিয়াশীল, আর O হল তুলাদণ্ডের আলম্ব । তুলাদণ্ড অনুভূমিক হলে বলবিদ্যার সূত্রানুসারে বস্তুর ওজন x AO = বাটখারার ওজন x BO । যেহেতু AO = BO, এতএব বস্তুর ওজন = বাটখারার ওজন । অর্থাৎ, বস্তুর ভর = বাটখারার ভর । বাটখারার ওপর লেখা ওজন সংখ্যা পাঠ করে বস্তুর ওজন প্রকাশ করা হয় ।
ভালো তুলাযন্ত্রের বৈশিষ্ট্য সমূহ :
(1) তুলাযন্ত্রটি সুবেদী হবে অর্থাৎ, তুলাযন্ত্রটি দুই তুলা পাত্রে রাখা ভরের সূক্ষ্ম পার্থক্য নির্দেশ করতে সমর্থ হবে । তুলাযন্ত্রকে সুবেদী করা যায় –
(a) তুলাদন্ডকে লম্বা ও হালকা করে ।
(b) তুলা পাত্র গুলিকে হালকা করে ।
(c) তুলাদন্ডের আলম্ব ও ভারকেন্দ্রের মধ্যে দূরত্ব কম করে এবং
(d) সূচক লম্বা করে ।
(2) তুলাযন্ত্রটি নির্ভুল হবে অর্থাৎ, তুলাপাত্র দুটি খালি থাকা অবস্থায় তুলাদন্ডটি অনুভূমিক হবে ।
(3) তুলাযন্ত্রটি সুস্থিত হবে অর্থাৎ, ভর পরিমাপের সময়, তুলাদন্ড দুলতে শুরু করলে দ্রুত স্থির হবে ।
(4) তুলাযন্ত্রটি দৃঢ় হবে অর্থাৎ, যন্ত্রের বিভিন্ন অংশ মজবুত হবে ।
সাধারণ তুলাযন্ত্রে ভর পরিমাপের জন্য একটি আলাদা বাক্সে বাটখারা রাখা থাকে । বাটখারা গুলির ভর 1 : 2 : 2 : 5 এই অনুপাতে রাখা হয় । ফলে নির্দিষ্ট সীমার মধ্যে যে-কোনো ভর সবচেয়ে কম সংখ্যক বাটখারা ব্যবহার করে পরিমাপ করা সম্ভব হয় ।
একটি সাধারণ তুলাযন্ত্রের তুলাদণ্ডের দুই বাহুর দৈর্ঘ্য সমান, কিন্তু তুলাপাত্র দুটির ভর আলাদা । এরকম সাধারণ তুলাযন্ত্রের সাহায্যে কোনো বস্তুর সঠিক ভর কীভাবে নির্ণয় করা হয় ?
ধরা যাক তুলাযন্ত্রটির বাম ও ডানদিকের ভর যথাক্রমে M1 ও M2 এবং বস্তুর প্রকৃত ভর m । বস্তুটিকে বাম পাত্রে রেখে, ডান পাত্রে m1 ভরের বাটখারা চাপালে তুলাদণ্ড অনুভূমিক হয় ।
[tex] \therefore {M_1} + m = {M_2} + {m_1}[/tex] ......(1)
আবার বস্তুটিকে ডান পাত্রে রাখলে, এবং বাম পাত্রে m2 ভরের বাটখারা চাপালে তুলাদণ্ড অনুভূমিক হয় ।
[tex]\therefore {M_1} + {m_2} = {M_2} + m[/tex] ......(2)
(1) নং - (2) নং করে পাওয়া যায়, [tex]m - {m_2} = {m_1} - m[/tex]
বা [tex]2m = {m_1} + {m_2}[/tex]
বা [tex]m = \frac{{{m_1} + {m_2}}}{2}[/tex]
একটি সাধারণ তুলাযন্ত্রের তুলাদণ্ডের দুই বাহুর দৈর্ঘ্য অসমান, কিন্তু তুলাপাত্র দুটির ভর সমান । এরকম সাধারণ তুলাযন্ত্রের সাহায্যে কোনো বস্তুর সঠিক ভর কীভাবে নির্ণয় করা হয় ?
ধরা যাক তুলাযন্ত্রটির বামদিক ও ডানদিকের বাহুর দৈর্ঘ্য যথাক্রমে x ও y এবং বস্তুর প্রকৃত ভর m ।
বস্তুটিকে বাম পাত্রে রাখলে এবং ডানপাত্রে m1 ভরের বাটখারা চাপালে তুলাদণ্ড অনুভূমিক হয় । ওই স্থানের অভিকর্ষজ ত্বরণ g হলে,
[tex]mxg = {m_1}yg[/tex] .....(1)
আবার বস্তুটিকে ডানপাত্রে রাখলে এবং বামপাত্রে m2 ভরের বাটখারা চাপালে তুলাদণ্ড অনুভূমিক হয় ।
[tex]\therefore {m_2}xg = myg[/tex] .......(2)
(1) নং ÷ (2) নং করে পাওয়া যায়,
[tex]\frac{{mxg}}{{{m_2}xg}} = \frac{{{m_1}yg}}{{myg}}[/tex]
বা, [tex]\frac{m}{{{m_2}}} = \frac{{{m_1}}}{m}[/tex]
বা, [tex]{m^2} = {m_1}{m_2}[/tex] বা, [tex]m = \sqrt {{m_1}{m_2}} [/tex]
*****






