সমকোণী চৌপল বা আয়তঘন (Rectangular Parallelepiped)
সূচনা (Introduction) :- প্রাত্যহিক জীবনে আমাদের নানা প্রকার ঘনবস্তু নিজেদের প্রয়োজনে ব্যবহার করতে হয় । এই ধরণের ঘনবস্তু গুলি কোনটি সুষম এবং কোনটি অসম । এই সমস্ত ঘনবস্তুগুলির আকৃতি সম্মন্ধে পূর্বে আমাদের পরিচয় ঘটেছে । শুধু তাই নয় এই সব ঘনবস্তু গুলির একটি তল থেকে যে ক্ষেত্র পাওয়া যায় তাদের সঙ্গেও পরিচয় ঘটেছে । এখন আমরা একটি বিশেষ ধরণের ঘনবস্তুর মাত্রাগুলির সঙ্গে পরিচয় করে, তার থেকে সমগ্র তলের ক্ষেত্রফল ও আয়তন নির্ণয় করব ।
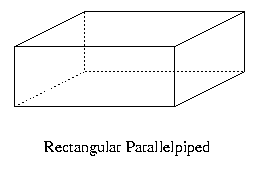
সমকোণী চৌপল বা আয়তঘন (Rectangular Parallelepiped) :- যে ঘন বস্তুর প্রতিটি তল আয়তকার, তলগুলি প্রত্যেকটি তার পাশের তলের সঙ্গে সমকোণে থাকে এবং বিপরীত তলের সঙ্গে সমান্তরাল থাকে, সেই ঘনবস্তুকে সমকোণী চৌপল বা আয়তঘন বলে ।
আমাদের বই, জ্যামিতির বাক্স, ইট ইত্যাদির তিনটি মাত্রা আছে । মাত্রা গুলি হল দৈর্ঘ্য, প্রস্থ এবং উচ্চতা । এগুলি সাধারণভাবে সমকোণী চৌপল বা আয়তঘনর উদাহরণ । আয়তঘনের দুটি তলের ছেদ রেখাংশকে ধার বা প্রান্তিকী বলা হয় ।
লক্ষ্য করো , সাধারণভাবে ঘরের মেঝে ও দেওয়াল পরস্পর সমকোণে থাকে । আবার, পাকা ঘরের চাদ এবং মেঝে হল দুটি সমান্তরাল তলের উদাহরণ ।
উপরের চিত্রে লক্ষ্য করলে দেখা যায় মাত্রার সংখ্যা হল 3টি, শীর্ষবিন্দু 8টি , ধার 12টি , তল 6টি এবং প্রতিটি তল আয়তকার । সমকোণী চৌপলটি যে তলের উপর দাঁড়িয়ে থাকে তাকে সমকোণী চৌপলের ভূমি বলে । ভূমি সংলগ্ন বড় বাহুটিকে দৈর্ঘ্য এবং ছোটোটিকে প্রস্থ বলে, তৃতীয় মাত্রাটিকে উচ্চতা বা বেদ বলে ।
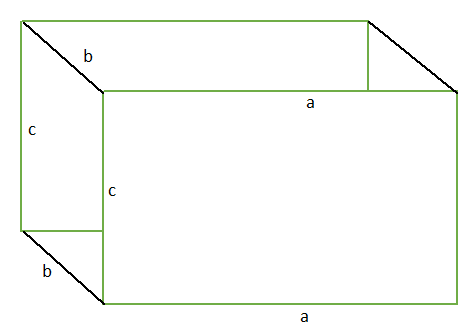
সমকোণী চৌপল বা আয়তঘনের সমগ্রতলের ক্ষেত্রফল (Area of Rectangular Parallelepiped)
= ছয়টি আয়তকার তলের ক্ষেত্রফল
= 2 ( দৈর্ঘ্য [tex] \times [/tex] প্রস্থ + প্রস্থ [tex] \times [/tex] উচ্চতা + উচ্চতা [tex] \times [/tex] দৈর্ঘ্য )
= 2 ( ab +bc +ca )
সমকোণী চৌপলের আয়তন (Volume of Rectangular Parallelepiped)
সমকোণী চৌপলের আয়তন বলতে বস্তুটি যে পরিমান পদার্থ দিয়ে তৈরি তা বোঝায়। আয়তন মাপার সাধারণ সূত্র হল
= ( ভূমির ক্ষেত্রফল [tex] \times [/tex] উচ্চতা )
অতএব সমকোণী চৌপলের আয়তন
= ( দৈর্ঘ্য [tex] \times [/tex] প্রস্থ ) [tex] \times [/tex] উচ্চতা
= [tex]\left( {a \times b} \right) \times c[/tex]
সমকোণী চৌপলের কর্ণ নির্ণয় (To find Diagonal of Rectangular Parallelepiped)
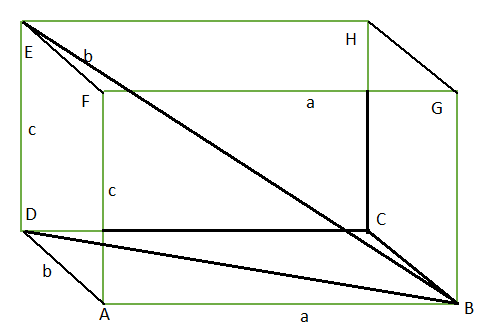
সমকোণী চৌপলের কর্ণ
[tex]\begin{array}{l} = \sqrt {B{D^2} + D{E^2}} \\ = \sqrt {\left( {A{B^2} + A{D^2}} \right) + D{E^2}} \\ = \sqrt {{a^2} + {b^2} + {c^2}} \end{array}[/tex]
মন্তব্য দৈর্ঘ্য , প্রস্থ এবং উচ্চতা কখনো ঋণাত্মক হতে পারে না তাই কর্ণের দৈর্ঘ্য সবসময় ধনাত্মক হয় ।
