লম্ব পিরামিড (Right Pyramid)
পিরামিডের সংজ্ঞা (Definition of Pyramid)
 যে বহুতলকের একটিমাত্র প্রান্ততল থাকে এবং পার্শ্বতলগুলি প্রত্যেকটি ত্রিভুজাকার হয় এবং তাদের একটি সাধারণ শীর্ষবিন্দু থাকে, তবে সেই বহুতলককে পিরামিড (Pyramid) বলে । পিরামিডের প্রান্ততলটিকে ভূমি (Base) বলে এবং পার্শ্বতলগুলির অর্থাৎ ত্রিভুজের সাধারণ শীর্ষবিন্দুটিকে শীর্ষ (Vertex) বলে । শীর্ষ থেকে ভূমির উপরে অঙ্কিত লম্বকে উচ্চতা (Height) বলে । প্রতি দুটি ত্রিভুজাকার পার্শ্বতল যে রেখায় ছেদ করে তাকে পার্শ্বপ্রান্তিকী (Slant Edge) বলে ।
যে বহুতলকের একটিমাত্র প্রান্ততল থাকে এবং পার্শ্বতলগুলি প্রত্যেকটি ত্রিভুজাকার হয় এবং তাদের একটি সাধারণ শীর্ষবিন্দু থাকে, তবে সেই বহুতলককে পিরামিড (Pyramid) বলে । পিরামিডের প্রান্ততলটিকে ভূমি (Base) বলে এবং পার্শ্বতলগুলির অর্থাৎ ত্রিভুজের সাধারণ শীর্ষবিন্দুটিকে শীর্ষ (Vertex) বলে । শীর্ষ থেকে ভূমির উপরে অঙ্কিত লম্বকে উচ্চতা (Height) বলে । প্রতি দুটি ত্রিভুজাকার পার্শ্বতল যে রেখায় ছেদ করে তাকে পার্শ্বপ্রান্তিকী (Slant Edge) বলে ।
কোনো সমতলে অবস্থিত একটি বিন্দু থেকে অঙ্কিত কোনো সরলরেখা যদি ওই বিন্দু দিয়ে ওই সরলরেখার উপরে অবস্থিত সকল সরলরেখার উপর লম্ব হয়, তবে প্রথম সরলরেখাটিকে সমতলটির উপরে লম্ব বলে ।
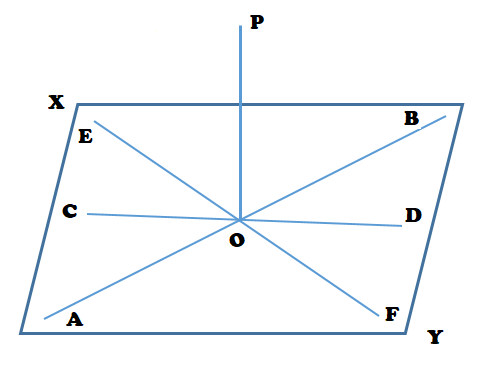
উপরের চিত্রটিতে [tex]PO \bot XY[/tex] সমতল অর্থাৎ [tex]PO \bot AB,PO \bot CD,PO \bot EF..........[/tex] . প্রকৃতপক্ষে O বিন্দুগামী XY সমতলস্থ দুটি সরলরেখার উপর PO লম্ব হলেই PO, XY সমতলের উপরে লম্ব হবে । কোনো পিরামিডের শীর্ষ থেকে ভূমির উপরে অঙ্কিত লম্ব যদি ভূমির যে বহুভুজ তার অন্তর্বৃত্ত বা পরিবৃত্তের কেন্দ্র দিয়ে যায় (অর্থাৎ উচ্চতার পদবিন্দু ভূমির অন্তর্বৃত্ত বা পরিবৃত্তের কেন্দ্র হলে) তবে পিরামিডটিকে লম্ব পিরামিড (Right Pyramid) বলে, অন্যথায় তির্যক পিরামিড বলে । লম্ব পিরামিডের ভূমি সুষম ক্ষেত্র হলে পিরামিডটিকে সুষম পিরামিড বলে ।
আমাদের আলোচনা এখানে লম্ব ও সুষম পিরামিডের মধ্যে সীমাবদ্ধ থাকবে। তাই শুধু পিরামিড উল্লেখ থাকলে লম্ব ও সুষম পিরামিডকেই বুঝতে হবে ।
পিরামিডের শীর্ষ থেকে ভূমির যেকোনো বাহুর উপর অঙ্কিত লম্বকে পিরামিডের তির্যক উচ্চতা (Slant Height) বলা হয় । পিরামিডের প্রত্যেকটি তির্যক উচ্চতাই সমান । তারা ভূমির যে বাহুর উপরে লম্ব তাকে সমদ্বিখণ্ডিত করে এবং পিরামিডের প্রত্যেকটি পার্শ্বতল সর্বসম ।
পিরামিডের ভূমির বাহুসংখ্যা n হলে, পার্শ্বতল সংখ্যা n, মোট তলসংখ্যা n + 1, পার্শ্বপ্রান্তিকীর সংখ্যা n, তির্যক উচ্চতার সংখ্যা n এবং মোট প্রান্তিকীর সংখ্যা হবে 2n ।
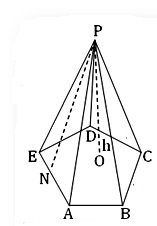
উপরের চিত্রে পিরামিডের ভূমি হল ABCDE, যা একটি পঞ্চভুজ । পিরামিডের পার্শ্বতলগুলি হল ABP, BPC, CDP, DEP এবং EPA । পার্শ্বপ্রান্তিকীগুলি হল AP, BP, CP, DP এবং EP । প্রান্তিকীগুলি হল AB, BC, CD, EA, AP, BP, CP, DP এবং EP । লম্ব উচ্চতা হল OP । EAP তলের তির্যক উচ্চতা দেখানো হয়েছে তা হল PN ।
পিরামিডের তল ও আয়তন পরিমাপ সংক্রান্ত সূত্রাবলি :-
1. পার্শ্বতলগুলির ক্ষেত্রফল = [tex]\frac{1}{2} \times [/tex] ভূমির পরিসীমা [tex] \times [/tex] তির্যক উচ্চতা
2. সমগ্রতলের ক্ষেত্রফল = পার্শ্বতলগুলির ক্ষেত্রফল + ভূমির ক্ষেত্রফল
3. আয়তন = [tex]\frac{1}{3} \times [/tex] ভূমির ক্ষেত্রফল [tex] \times [/tex] উচ্চতা
যে পিরামিডের ভূমি একটি ত্রিভুজ (স্বাভাবিকভাবেই তলসংখ্যা 4) তাকে চতুস্তলক (Tetrahedron) বলে ।
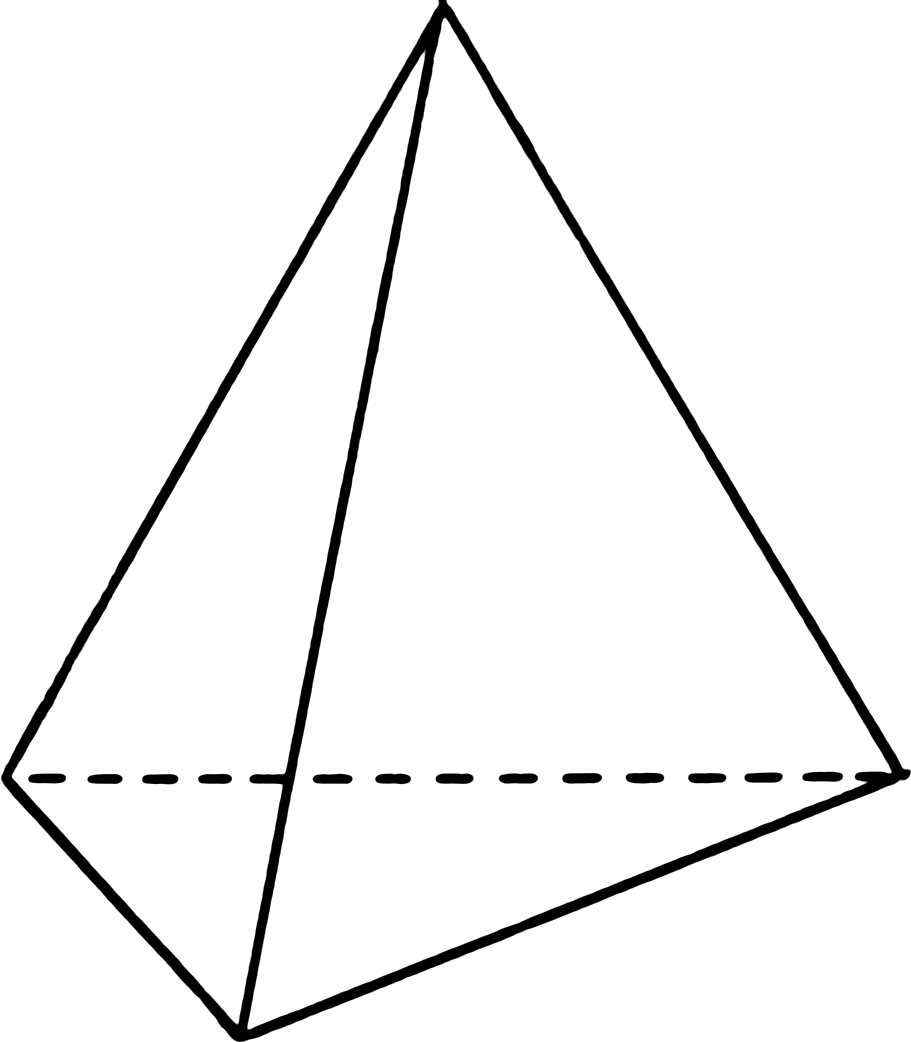
ইহার ভূমি সুষম অর্থাৎ সমবাহু ত্রিভুজ এবং পার্শ্বতলগুলি সর্বসম সমদ্বিবাহু ত্রিভুজ হলে, ইহাকে লম্ব চতুস্তলক (Right Tetrahedron) বলে । যে চতুস্তলকের চারটি তলই সর্বসম সমবাহু ত্রিভুজ তাকে সুষম লম্ব চতুস্তলক (Regular right Tetrahedron) বলে ।
**






