বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য

বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য

সূচনা (Introduction) : আমরা পূর্বেই জেনেছি একটি সরলরেখা একই সমতলে অবস্থিত একটি বৃত্তকে দুই এর অধিক বিন্দুতে ছেদ করতে পারে না । 

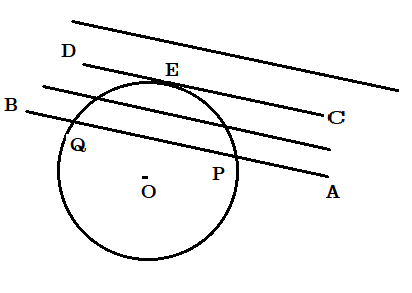পাশের চিত্রে AB সরলরেখাটি বৃত্তটিকে P, Q বিন্দুতে ছেদ করেছে । AB এর অবস্থানের সঙ্গে সমান্তরাল করে সরলরেখাটিকে বৃত্তের পরিধির দিকে ক্রমশ সরালে দেখাযায় ছেদ বিন্দু দুটি নিকটবর্তী হয় এবং AB এর অবস্থান যখন CD হয়, তখন ছেদবিন্দু সমাপতিত হয় E বিন্দুতে অর্থাৎ CD সরলরেখাটি বৃত্তটিকে ছুঁয়ে যায় বা স্পর্শ করে । CD কে বৃত্তের স্পর্শক এবং E বিন্দুকে বলে স্পর্শবিন্দু । এরপর দেখা যায় AB এর পরবর্তী অবস্থানে সরলরেখাটি বৃত্তটিকে কোনো বিন্দুতে ছেদ বা স্পর্শ করবে না । 

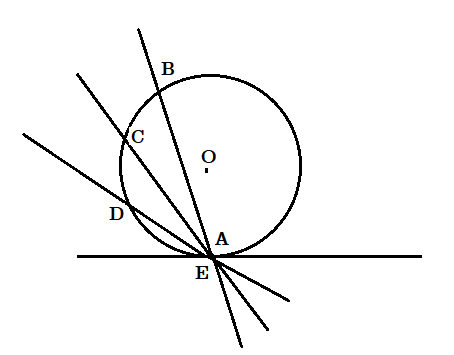
ডানদিকের চিত্রে একটি সরলরেখা বৃত্তটিকে A ও B বিন্দুতে ছেদ করেছে । A বিন্দুকে স্থির রেখে যদি সরলরেখাটিকে ঘোরানো হয় (চিত্রে ঘড়ির কাঁটার বিপরীতদিকে ঘোরানো হয়েছে) তাহলে দেখা যায় অপর ছেদ বিন্দুটি A বিন্দুর আরো নিকটবর্তী হয় । এভাবে ঘোরানোর ফলে সরলরেখাটির এমন একটি অবস্থান হবে যখন অপর ছেদ বিন্দুটি A বিন্দুর সাথে মিশে যাবে বা দুটি ছেদবিন্দু A বিন্দুতে সমাপ্তিটা হবে, তখন সরলরেখাটি A বিন্দুতে স্পর্শক হবে । 

নীচের চিত্র থেকে স্পর্শক সম্মন্ধে আমাদের আরো পরিষ্কার ধারণা হবে 

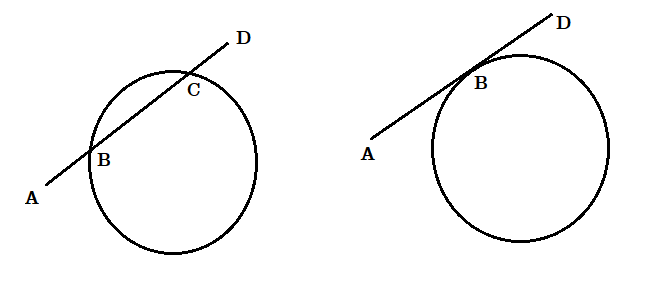
উপরের চিত্র থেকে দেখতে পাওয়া যায় যে AD সরলরেখা একটি বৃত্তকে B ও C বিন্দুতে ছেদ করেছে এবং অপর বৃত্তকে B বিন্দুতে স্পর্শ করেছে । প্রথমক্ষেত্রে AD কে বৃত্তের ছেদক বলে । দ্বিতীয়ক্ষেত্রে AD কে বৃত্তের স্পর্শক ও B বিন্দুকে স্পর্শবিন্দু বলে । AD স্পর্শকের উপরে B বিন্দু ছাড়া অন্য কোনো বিন্দু বৃত্তের উপর অবস্থিত নয় । 

বৃত্তের কোনো বিন্দুতে স্পর্শক ও ঐ স্পর্শবিন্দুগামী ব্যাসার্ধ পরস্পর লম্বভাবে অবস্থিত 

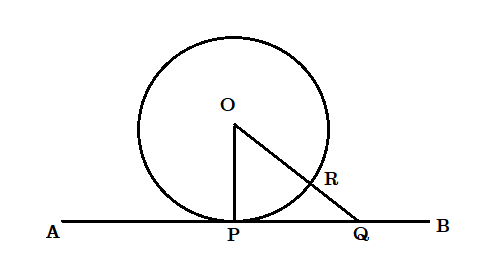মনে করি O কেন্দ্রীয় কোনো বৃত্তের P বিন্দুতে AB স্পর্শক এবং OP, P বিন্দুগামী ব্যাসার্ধ । আমাদের প্রমাণ করতে হবে যে OP এবং AB পরস্পর লম্ব । 

অঙ্কন : AB স্পর্শকের উপর অপর যেকোনো একটি বিন্দু Q নেওয়া হল । O , Q যুক্ত করা হল । 

প্রমাণ : যেহেতু স্পর্শক AB এর উপরে স্পর্শবিন্দু P ব্যাতিত অপর যেকোনো একটি বিন্দু Q বৃত্তের বাইরে অবস্থিত , সুতরাং OQ বৃত্তটিকে একটি বিন্দুতে ছেদ করবে । মনে করি ছেদবিন্দু হল R ।

অতএব OR < OQ (যেহেতু R বিন্দু O , Q এর অন্তর্বর্তী)

আবার OR = OP .(একই বৃত্তের ব্যাসার্ধ)

অতএব OP < OQ 

যেহেতু Q বিন্দু AB এর উপর যেকোনো বিন্দু , তাই O কেন্দ্র থেকে AB এর উপর যত রেখাংশ অঙ্কন করা যায় OP তাদের মধ্যে ক্ষুদ্রতম হবে । 

অতএব OP এবং AB পরস্পর লম্ব । 

অনুসিদ্ধান্ত 

1. বৃত্তের উপর অবস্থিত কোনো বিন্দুগামী ব্যাসার্ধের উপর ঐ বিন্দুতে অঙ্কিত লন্ব বৃত্তের স্পর্শক হবে । 
2. বৃত্তের উপর অবস্থিত কোনো বিন্দুতে একটিমাত্র স্পর্শক অঙ্কন করা যায়। ( যেহেতু ঐ বিন্দুতে ঐ বিন্দুগামী ব্যাসার্ধের উপর একটি মাত্র লম্ব অঙ্কন করা যায়)
3. স্পর্শবিন্দুতে স্পর্শকের উপর অঙ্কিত লম্ব বৃত্তের কেন্দ্রগামী হবে। কারণ একটি সরলরেখার উপর অবস্থিত একটি বিন্দুতে একটিমাত্র লম্ব অঙ্কন করা যায় । 

কয়েকটি প্রয়োগ 

(১) O কেন্দ্রীয় কোনো একটি বৃত্তের AB একটি ব্যাস। A বিন্দুতে বৃত্তের স্পর্শক PAQ . RS জ্যাটি স্পর্শক PAQ এর সমান্তরাল হলে প্রমাণ করো যে , AB , RS এর লম্ব সমদ্বিখণ্ডক । 

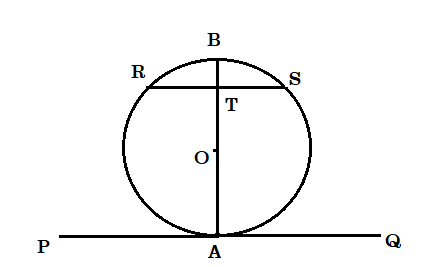প্রমাণ : মনে করি AB , RS কে T বিন্দুতে ছেদ করে । 

অতএব PAQ , O কেন্দ্রীয় বৃত্তের A বিন্দুতে স্পর্শক এবং AB ব্যাস , 

অতএব [tex]AB \bot PQ[/tex]

আবার PQ ।। RS এবং AB ভেদক । 

অতএব [tex]AB \bot RS[/tex]

অতএব T , RS এর মধ্যবিন্দু । ( যেহেতু OT কেন্দ্র থেকে জ্যা RS এর উপর লম্ব )

অতএব AB , RS এর লম্ব সমদ্বিখণ্ডক । 

(২) বৃত্তের বহিস্থ কোনো বিন্দু থেকে ওই বৃত্তে দুটি স্পর্শক অঙ্কন করা যায় । 

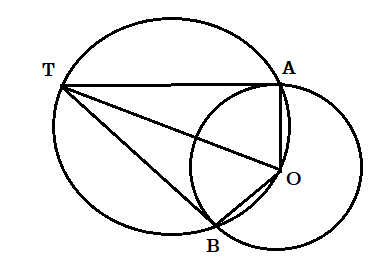O কেন্দ্রীয় একটি বৃত্তে T একটি বহিস্থ বিন্দু। প্রমাণ করতে হবে যে , T বিন্দু থেকে O কেন্দ্রীয় বৃত্তে দুটি স্পর্শক অঙ্কন করা যায় । 

অঙ্কন : T , O যুক্ত করা হল । TO কে ব্যাস করে একটি বৃত্ত অঙ্কন করা হল । T বিন্দু বৃত্তের বহিস্থ এবং O বিন্দু বৃত্তের অন্তঃস্থ বলে বৃত্তটি O কেন্দ্রীয় বৃত্তকে দুটি বিন্দুতে ছেদ করে । মনে করি ছেদবিন্দু দুটি হল A ও B . TA , TB , OA ও OB যুক্ত করা হল । 

প্রমাণ : [tex]\angle OAT[/tex] এবং [tex]\angle OBT[/tex] এরা প্রত্যেকেই অর্ধবৃত্তস্থ কোণ। 

অতএব [tex]\angle OAT = \angle OBT = {90^ \circ }[/tex]

অর্থাৎ [tex]TA \bot OA[/tex] এবং [tex]TB \bot OB[/tex]

অতএব TA ও TB যথাক্রমে O কেন্দ্রীয় বৃত্তের ব্যাসার্ধ OA এবং OB এর উপর লম্ব । 

অতএব TA ও TB O কেন্দ্রীয় বৃত্তে A ও B বিন্দুতে স্পর্শক । 

অতএব প্রমাণিত বৃত্তের বহিস্থ কোনো বিন্দু থেকে ওই বৃত্তে দুটি স্পর্শক অঙ্কন করা যায় । 

বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে যে দুটি স্পর্শক অঙ্কন করা যায় তাদের স্পর্শবিন্দু দুটির সাথে বহিঃস্থ বিন্দুর সংযোগ রেখাংশ দুটি সমান এবং তারা কেন্দ্রে সমান কোণ উৎপন্ন করে । 

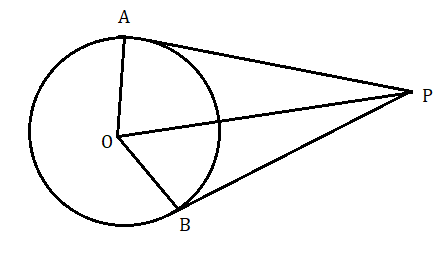ধরা যাক কোনো বৃত্তের বহিঃস্থ কোনো P বিন্দু থেকে PA এবং PB দুটি স্পর্শক অঙ্কন করা হল , যাদের স্পর্শ বিন্দু যথাক্রমে A ও B .O , A ; O , B এবং O , P যুক্ত করা হল । ফলে PA ও PB কেন্দ্র যথাক্রমে [tex]\angle POA[/tex] এবং [tex]\angle POB[/tex] কোণ উৎপন্ন করেছে । 

আমাদের প্রমাণ করতে হবে যে (i) PA = PB  (ii) [tex]\angle POA = \angle POB[/tex]

প্রমাণ : PA ও PB স্পর্শক এবং OA এবং OB হল স্পর্শবিন্দুগামী ব্যাসার্ধ । 

অতএব [tex]OA \bot PA[/tex] এবং [tex]OB \bot PB[/tex] 

PAO ও PBO সমকোণী ত্রিভুজদ্বয়ের OA =OB ( একই বৃত্তের ব্যাসার্ধ )

অতিভুজ OP সাধারণ বাহু .

ত্রিভুজ POA [tex] \cong [/tex] ত্রিভুজ PBO 

অতএব PA = PB ( অনুরূপ বাহু )

এবং [tex]\angle POA = \angle POB[/tex] ( অনুরূপ কোণ )

অনুসিদ্ধান্ত 

1. বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে অংকিত দুটি স্পর্শকের অন্তর্ভুত কোণকে ওই বিন্দু এবং কেন্দ্রের সংযোগ সরলরেখা সমদ্বিখণ্ডিত করে । 

2.বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে অংকিত স্পর্শক দুটির অন্তর্ভুত কোণের অন্তর্দ্বিখণ্ডক কেন্দ্রগামী হবে । 

3.বৃত্তের উপরিস্থ দুটি বিন্দুতে অংকিত স্পর্শক দুটি যদি পরস্পরকে ছেদ করে , তাহলে ছেদ বিন্দু থেকে স্পর্শ বিন্দু পর্যন্ত অঙ্কিত রেখাংশের দৈর্ঘ্য সমান হবে । 

কয়েকটি সংজ্ঞা 

সাধারণ স্পর্শক : একটি সরলরেখা যদি দুটি বৃত্তের প্ৰত্যেককে স্পর্শ করে , তাহলে ওই সরলরেখাটিকে বৃত্ত দুটির সাধারণ স্পর্শক বলে। নীচে সাধারণ স্পর্শকের কতগুলি নমুনা চিত্র দেখানো হল । 

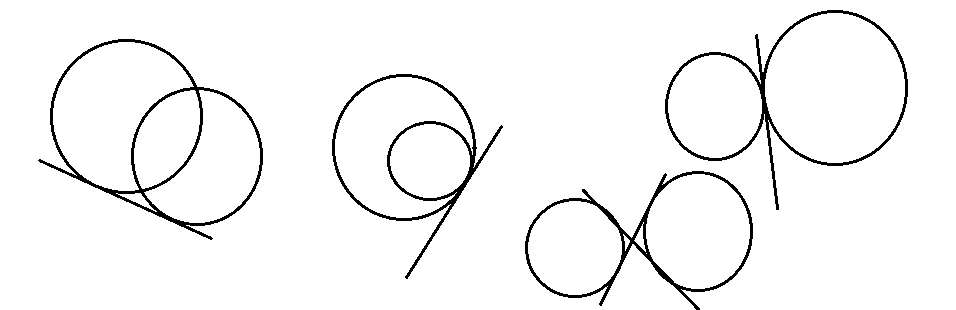
সরল সাধারণ স্পর্শক  : যে সাধারণ স্পর্শকের একই পাশে বৃত্ত দুটি অবস্থিত হয় তাকে সরল সাধারণ স্পর্শক বলে । 

তির্যক সাধারণ স্পর্শক  : যে সাধারণ স্পর্শকের বিপরীত পাশে বৃত্ত দুটি অবস্থিত হয় তাকে তির্যক সাধারণ স্পর্শক বলে । 

যদি দুটি বৃত্ত পরস্পরকে স্পর্শ করে তাহলে স্পর্শ বিন্দুটি কেন্দ্র দুটির সংযোগ সরলরেখার উপরে অবস্থিত হবে । 

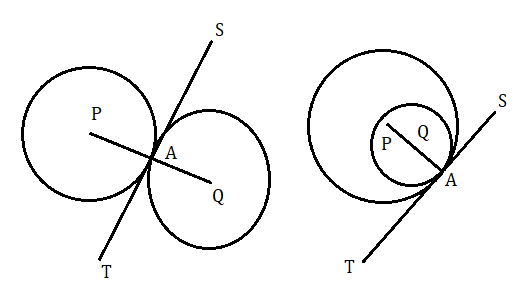
ধরা যাক P ও Q কেন্দ্রীয় দুটি বৃত্ত পরস্পরকে A বিন্দুতে স্পর্শ করেছে। প্রমাণ করতে হবে যে P , A ও Q সমরেখ । 

অঙ্কন : P , A ও Q , A যুক্ত করা হল । 

প্রমাণ : যেহেতু বৃত্ত দুটি A বিন্দুতে পরস্পরকে স্পর্শ করেছে। সুতরাং A বিন্দুতে একটি সাধারণ স্পর্শক আছে। মনে করি ST হল সাধারণ স্পর্শক যা দুটি বৃত্তকে A বিডিতে স্পর্শ করেছে । 

অতএব P কেন্দ্রীয় বৃত্তের ST স্পর্শক এবং PA কেন্দ্র বিন্দুগামী ব্যাসার্ধ।  অতএব [tex]PA \bot ST[/tex]

আবার Q কেন্দ্রীয় বৃত্তের ST স্পর্শক এবং QA স্পর্শ বিন্দুগামী ব্যাসার্ধ।  অতএব [tex]QA \bot ST[/tex]

অতএব PA ও QA একই বিন্দুতে ST এর উপর লম্ব । 

অতএব PA ও QA একই সরলরেখার উপর অবস্থিত , অর্থাৎ P , A , Q বিন্দু তিনটি সমরেখ । 

 

অনুসিদ্ধান্ত :

(১) দুটি বৃত্ত পরস্পরকে স্পর্শ করলে , একটির কেন্দ্র ও স্পর্শবিন্দুগামী সরলরেখা অপর বৃত্তের কেন্দ্র দিয়ে যাবে। 

(২) দুটি বৃত্ত বহিঃস্পর্শ করলে , কেন্দ্র দুটির দূরত্ব ব্যাসার্ধ দুটির দৈঘ্যের সমষ্টি হবে। 

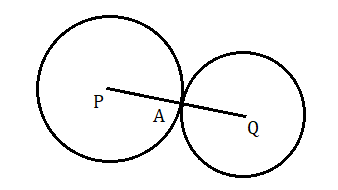
দেখা যাচ্ছে PQ = PA + QA 

(৩)  দুটি বৃত্ত অন্তস্পর্শ করলে , কেন্দ্র দুটির দূরত্ব ব্যাসার্ধ দুটির দৈঘ্যের অন্তরফলের সমান হবে । 

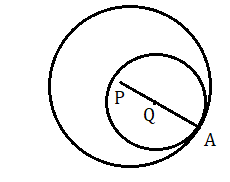
দেখা যাচ্ছে PQ = PA - QA 

কয়েকটি প্রয়োগ 

(১) O কেন্দ্রীয় বৃত্তে AB ব্যসের A ও B বিন্দুতে অঙ্কিত দুটি সমান্তরাল স্পর্শক বৃত্তটির অপর একটি বিন্দু T তে অঙ্কিত স্পর্শকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে। প্রমাণ করতে হবে যে [tex]\angle POQ = {90^ \circ }[/tex]

প্রমাণ : O কেন্দ্রীয় বৃত্তে A ও T বিন্দুতে অঙ্কিত স্পর্শক দুটি P বিন্দুতে 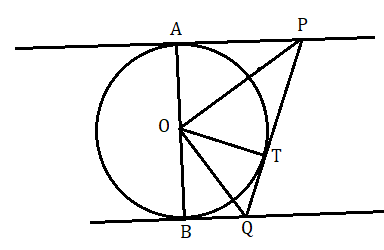ছেদ করে । 

অতএব PO , [tex]\angle APT[/tex] এর অন্তর্দ্বিখণ্ডক । 

অর্থাৎ [tex]\angle TPO = \frac{1}{2}\angle APT[/tex]

অনুরূপে T ও B বিন্দুতে অঙ্কিত স্পর্শক দুটি Q বিন্দুতে ছেদ করেছে । 

অতএব [tex]\angle TQO = \frac{1}{2}\angle BQT[/tex]

আবার AP ।। BQ এবং ভেদক PQ 

অতএব 

[tex]\begin{array}{l}
\angle BQT + \angle APT = {180^ \circ }\\
 \Rightarrow 2\angle TQO + 2\angle TPO = {180^ \circ }\\
 \Rightarrow \angle TQO + \angle TPO = {90^ \circ }
\end{array}[/tex]

সুতরাং ত্রিভুজ POQ এর অপর কোণটি [tex]\angle POQ = {90^ \circ }[/tex]

 

(২) কেন্দ্রীয় বৃত্তের পরিলিখিত চতুর্ভুজ ABCD . প্রমাণ করতে হবে যে AB + CD = BC + DA 

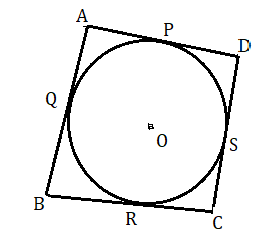ABCD চতুর্ভুজটি O কেন্দ্রীয় বৃত্তে পরিলিখিত। মনে করি AB , BC , CD এবং DA বৃত্তটিকে যথাক্রমে Q , R , S এবং P বিন্দুতে স্পর্শ করেছে । আমাদের প্রমাণ করতে হবে যে AB + CD = BC + DA .

প্রমাণ : O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু A থাকে AP ও AQ দুটি স্পর্শক। সুতরাং AP = AQ .

অনুরূপে BQ = BR ; CR = CS এবং DS = DP .

অতএব AQ + BQ + CS + DS = AP + BR + CR + DP 

অর্থাৎ , AB + CD = AP + DP + BR + CR = BC + DA 

 

(৩) P ও Q কেন্দ্র বিশিষ্ট দুটি বৃত্ত পরস্পরকে A বিন্দুতে বহিঃস্পর্শ করেছে। বৃত্ত দুটির একটি সরল সাধারণ স্পর্শক দুটি বৃত্তকে যথাক্রমে R এবং S বিন্দুতে স্পর্শ করেছে। প্রমাণ করতে হবে যে 

(i) A বিন্দুতে অঙ্কিত সাধারণ স্পর্শক RS রেখাংশ কে T বিন্দুতে সমদ্বিখণ্ডিত করে । 

(ii) [tex]\angle RAS = {90^ \circ }[/tex]

(iii) যদি PT ও QT , AR ও AS কে যথাক্রমে C ও B বিন্দুতে ছেদ করে , তাহলে ABTC একটি আয়তক্ষেত্র হবে । 

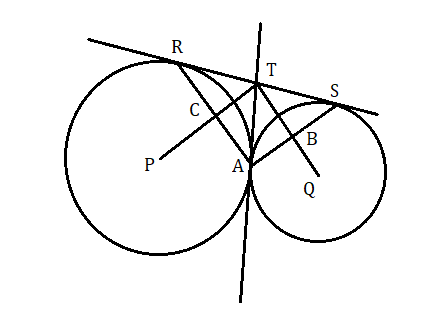প্রমাণ : A বিন্দুতে অঙ্কিত স্পর্শক RS কে T বিন্দুতে ছেদ করেছে । 

অতএব T বিন্দু থেকে P কেন্দ্রীয় বৃত্তে দুটি স্পর্শক TR ও TA .

অতএব TR = TA .

অনুরূপভাবে TS = TA . অতএব TR = TS .

এর থেকে বলা যায় যে AT , RS কে সমদ্বিখণ্ডিত করে। 

আবার ত্রিভুজ ATR এর TR = TA  অতএব [tex]\angle TAR = \angle TRA[/tex]

অনুরূপভাবে [tex]\angle TAS = \angle TSA[/tex]

অতএব 

[tex]\begin{array}{l}
\angle RAS = \angle TAR + \angle TAS\\
 \Rightarrow \angle RAS = \angle TRA + \angle TSA\\
 \Rightarrow \angle RAS = {90^ \circ }
\end{array}[/tex]

আবার PT , [tex]\angle RTA[/tex] এর সমদ্বিখণ্ডক এবং QT , [tex]\angle ATS[/tex] এর সমদ্বিখণ্ডক। 

অতএব [tex]PT \bot QT[/tex] অর্থাৎ [tex]\angle PTQ = {90^ \circ }[/tex]

আবার [tex]PT \bot RA[/tex] এবং [tex]QT \bot SA[/tex]

অতএব [tex]\angle ACT = \angle ABT = {90^ \circ }[/tex]

সুতরাং প্রমাণিত ABTC একটি আয়তক্ষেত্র । 

 

(৪) দুটি বৃত্ত পরস্পরকে O বিন্দুতে বহিঃস্পর্শ করে। PQ এবং RS দুটি বৃত্তের ব্যাস এবং পরস্পর সমান্তরাল। প্রমাণ করতে হবে যে P , O এবং S সমরেখ । 

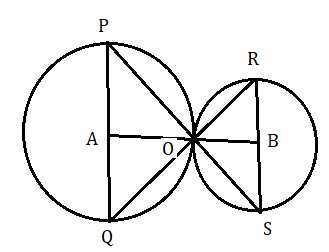প্রমাণ : মনে করি বৃত্ত দুটির কেন্দ্র যথাক্রমে A ও B . O বিন্দুতে বৃত্ত দুটি পরস্পরকে বহিঃস্পর্শ করেছে । 

অতএব A , O , B একই সরলরেখায় অবস্থিত হবে । 

ত্রিভুজ PAO এর [tex]\angle APO = \angle AOP[/tex] ( যেহেতু AP = AO একই বৃত্তের ব্যাসার্ধ )

আবার 

[tex]\begin{array}{l}
\angle APO + \angle AOP + \angle PAO = {180^ \circ }\\
 \Rightarrow 2\angle AOP = {180^ \circ } - \angle PAO
\end{array}[/tex]

অনুরূপে [tex]2\angle ROB = {180^ \circ } - \angle RBO[/tex]

অতএব

[tex]\begin{array}{l}
2\left( {\angle AOP + \angle ROB} \right) = {360^ \circ } - \left( {\angle PAO + \angle RBO} \right)\\
 \Rightarrow 2\left( {\angle AOP + \angle ROB} \right) = {360^ \circ } - {180^ \circ } = {180^ \circ }\\
 \Rightarrow \angle AOP + \angle ROB = {90^ \circ }
\end{array}[/tex]

আবার [tex]\angle POR = {180^ \circ } - \left( {\angle POA + \angle ROB} \right) = {180^ \circ } - {90^ \circ } = {90^ \circ }[/tex]

এবং [tex]\angle POR + \angle ROS = {90^ \circ } + {90^ \circ } = {180^ \circ }[/tex] ( যেহেতু [tex]\angle ROS[/tex] অর্ধবৃত্তস্থ কোণ )

অতএব P , O এবং S সমরেখ । 

*****