ত্রিকোণমিতি (Trigonometry)

ত্রিকোণামিতি (Trigonometry)

সূচনা (Introduction):- ত্রিকোণমিতি বিষয়টি কী এবং কেন এর প্রয়োজনীতা তা আমাদের মধ্যে এই প্রশ্ন গুলি আসে । আমরা জানি " Necessity is the mother of invention " । প্রয়োজনের তাগিদ বড়ো তাগিদ । তাই গণিতের একটি বিশেষ শাখা ত্রিকোণমিতির জন্মের পিছনে প্রয়োজনের তাগিদ খুঁজলে বোধ হয় অন্যায় হবে না । কিন্তু কী সেই তাগিদ ?

প্রকৃতিতে মানুষ যা দেখতে পায় তা সব কিছু সে যাচাই করে নিতে চায়, তা সে হাতের কাছের গাছপালা, ফলমূল, জীবজন্তু থেকে আরম্ভ করে দূর দিগন্তের সূর্য, চন্দ্র, গ্রহ, নক্ষত্র, দুরারোহ পর্বতশৃঙ্গ, বিস্তীর্ন সমুদ্র, নদনদী যাই হোকনা কেন । এক সময় মানুষ তার হাতের কাছের সব জিনিস মাপতে শিখেছে, জ্যামিতির না না বস্তুর সাহায্যে বিভিন্ন বস্তুর আকৃতি বুঝতে শিখেছে, পরিমাপ করতে শিখেছে তাদের দৈর্ঘ্য, প্রস্থ, বেদ ইত্যাদি । আবার তারই সাহায্যে সে হাতের নাগালের বাইরের জিনিস যেমন গ্রহ, নক্ষত্র, সূর্য, চন্দ্র ইত্যাদির আকার আয়তন, দূরত্ব ইত্যাদির পরিমাপ করার এবং তাদের গতিসূত্র জানার চেষ্টা চালিয়েছে অনবরত । সেই প্রচেষ্টার ফলে গণিতজ্ঞরা পিরামিডের মাথায় না উঠেও মাটিতে দাঁড়িয়ে তার উচ্চতা নির্ণয় করে ছিলেন । এই ধরণের সমস্যার গাণিতিক সমাধান কিভাবে করা যায় তা ত্রিকোণমিতির অধ্যায়ে আমরা আলোচনা করব । 

নিচের চিত্রে দেখানো হয়েছে OP একটি লাইট পোস্ট । এর উচ্চতা আমাদের নির্ণয় করতে হবে । 

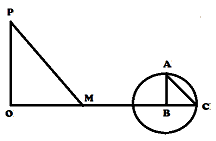
 লাইট পোস্ট থেকে কিছু দূরে লাইট পোস্টের ভূমির সমতলে AB একটি খুঁটি পোতা হল । B কে কেন্দ্র করে AB এর সমান ব্যাসার্ধ নিয়ে মাটিতে একটি বৃত্ত আঁকা হল । সকালের দিকে যখন সূর্য উঠছে তখন দেখা যাবে লাইট পোস্ট ও খুঁটির উভয়ের লম্বা ছায়া পড়েছে। সূর্য যত উপরে উঠতে থাকবে ছায়াও তত ছোট হতে থাকবে । এক সময় দেখা যাবে AB খুঁটির ছায়ার অগ্রভাগ, অর্থাৎ A বিন্দুর ছায়া C বিন্দুর সঙ্গে মিলে যাবে আর সেই সময়ে লাইট পোস্টের P বিন্দুর ছায়া M বিন্দুতে পড়েছে । 

এখন M বিন্দু থেকে লাইট পোস্টের পাদদেশ O এর দূরত্ব OM যা আমরা মাপতে পারি । আবার OM = OP  সুতরাং OM এর পরিমাপ করে আমরা লাইট পোস্টের উচ্চতা নির্ণয় করতে পারি । এখানে যে তত্ত্ব টি প্রয়োগ করা হয়েছে তা হল সদৃশকোণী ত্রিভুজের বাহুগুলি অনুপাতের সমতার তত্ত্ব । 

আমরা জানি বহুদূর থেকে আগত সূর্যরাশি কার্যত সমান্তরাল । সুতরাং PM।। AC । সুতরাং [tex]\angle PMO = \angle ACB[/tex] অতএব সমকোণী ত্রিভুজ ABC সদৃশকোণী । 

সমকোণী ত্রিভুজ ABC তে AB = BC । কারণ AB এর সমান ব্যাসার্ধ নিয়ে বৃত্ত টি আঁকা হয়েছে এবং BC বৃত্তের ব্যাসার্ধ । 

সুতরাং [tex]\frac{{AB}}{{BC}} = 1[/tex]

আবার যেহেতু ত্রিভুজ ABC ও ত্রিভুজ PMO সদৃশকোণী 

অতএব [tex]\frac{{PO}}{{OM}} = \frac{{AB}}{{BC}} = 1[/tex]

সুতরাং PO = OM 

তাহলে দেখা যাচ্ছে লাইট পোস্টের চূড়ায় না উঠেও মাটিতে দাঁড়িয়ে পোস্টের উচ্চতা নির্ণয় করা যায় ।