গোলক (Sphere)

গোলক (Sphere)

সূচনা (Introduction) :- আমরা প্রত্যেকেই ফুটবল, ভূগোলক, ক্রিকেট বল বা খেলার মার্বেল দেখেছি । এগুলোই আমাদের প্রাত্যহিক জীবনে দেখা গোলকের উদাহরণ । গোলক এমন একটি ঘনবস্তু যা একটি মাত্র বক্রতল দিয়ে তৈরী । 

গোলকের সাথে সম্পর্কিত কয়েকটি সংজ্ঞা (Some definitions which related to Sphere)

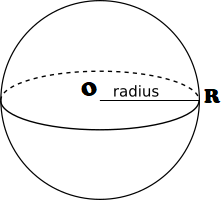
(1) গোলকের কেন্দ্র (Center of Sphere):- গোলকের কেন্দ্র হল গোলকের অভ্যন্তরে অবস্থিত এমন একটি নির্দিষ্ট বিন্দু যা থেকে গোলকের উপরিতলে অবস্থিত যেকোনো বিন্দুর দূরত্ব সমান । উপরের চিত্রে 'O' হল গোলকের কেন্দ্র । 

(2) গোলকটির ব্যাসার্ধ (Radious of Sphere):-  গোলকের কেন্দ্র থেকে গোলকের উপরিতলে অবস্থিত যেকোনো বিন্দুর দূরত্বকে গোলকটির ব্যাসার্ধ বলা হয় । উপরের চিত্রে OR হল গোলটির ব্যাসার্ধ । 

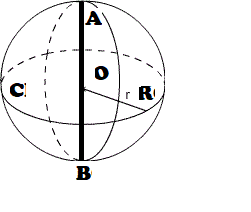
উপরের চিত্রে একটি ভূগোলকের রেখাচিত্র দেওয়া হয়েছে । AB যার দন্ড এবং AB দন্ডটি O কেন্দ্র দিয়ে গিয়ে গোলকের উপরিতলে A এবং B বিন্দুতে মিলেছে । AB রেখাকে গোলকের অক্ষ বলা হয় । একটু লক্ষ্য করলে দেখা যাবে AB কে স্থির রেখে তার উপরে দন্ডায়মান ACB অধিবৃত্তটির আবর্তনের ফলেই গোলকটি তৈরী হয়েছে অর্থাৎ ব্যাসকে অক্ষ ধরে কোনো অধিবৃত্তকে তার চতুর্দিকে ঘোরালে যে ঘনবস্তুটি তৈরী হয় তাকে গোলক (Sphere) বলে । 

গোলকের সমগ্রতলের ক্ষেত্রফল নির্ণয় (Calculate the area of a Sphere) :-

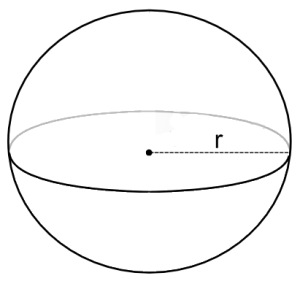গোলকের ব্যাসার্ধ যদি r হয় তবে ব্যাস হবে ( r + r ) = 2r এবং গোলকের বক্রপৃষ্ঠের ক্ষেত্রফল [tex] = \pi  \times {\left( {2r} \right)^2} = 4\pi {r^2}[/tex]

গোলক যেহেতু একটিমাত্র বক্রতল দিয়ে তৈরি তাই গোলকের সমগ্রতলের ক্ষেত্রফল [tex] = 4\pi {r^2}[/tex]

গোলকের আয়তন বা ঘনফল নির্ণয় (Calculate the volume of a Sphere)

গোলকের আয়তন বা ঘনফল [tex] = \frac{4}{3}\pi {r^3}[/tex]