অনুপাত ও সমানুপাত
অনুপাত ও সমানুপাতে সঙ্গে আমাদের আগে পাটিগণিত ও বীজগণিতে পরিচয় হয়েছে। জ্যামিতিতে এই ধারণা কিভাবে প্রয়োগ করা যায় , তার আলোচনাই আমরা করব।
কয়েকটি প্রয়োজনীয় জ্যামিতি
(১) যদি দুটি ত্রিভুজের ভূমি একই সরলরেখায় অবস্থিত হয় এবং ত্রিভুজদ্বয়ের ভূমির বিপরীত শীর্ষবিন্দু দুটি একই বিন্দু হয় তাহলে ত্রিভুজ দুটির ক্ষেত্রফলের অনুপাত ভূমির অনুপাতের সমান হবে।
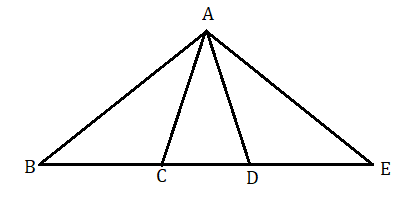মনে করি ত্রিভুজ ABC এবং ত্রিভুজ ADE এর ভূমি BC ও DE একই সরলরেখা BE এর উপর অবস্থিত এবং A উভয় ত্রিভুজেরই শীর্ষবিন্দু।
অতএব ত্রিভুজ ABC : ত্রিভুজ ADE = BC : DE
(২) যেকোনো ত্রিভুজের যেকোনো বাহুর সমান্তরাল সরলরেখা ওপর দুটি বাহুকে বা বর্ধিত বাহুকে সমানুপাতে বিভক্ত করে।
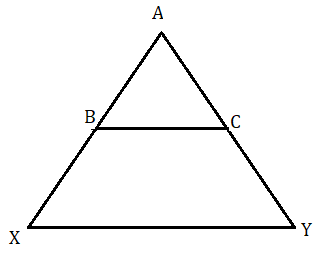
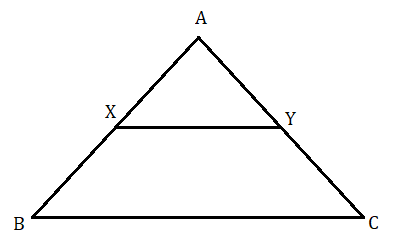মনে করি ত্রিভুজ ABC এর BC বাহুর সমান্তরাল সরলরেখা AB ও AC বাহুদ্বয়কে যথাক্রমে X ও Y বিন্দুতে সহিদ করেছে।
অতএব শর্তানুযায়ী
AX : XB = AY : YC
অর্থাৎ [tex]\frac{{AX}}{{XB}} = \frac{{AY}}{{YC}}[/tex]
ডান পাশের চিত্র থেকে দেখা যাচ্ছে XY সরলরেখা AB ও AC কে অন্তর্বিভক্ত করেছে।
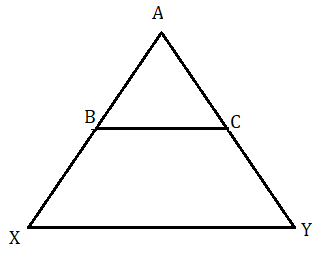বামপাশের চিত্র থেকে দেখা যায় XY সরলরেখা AB ও AC কে বহিঃর্বিভক্ত করেছে। এক্ষেত্রেও
AX : XB = AY : YC
অর্থাৎ [tex]\frac{{AX}}{{XB}} = \frac{{AY}}{{YC}}[/tex]
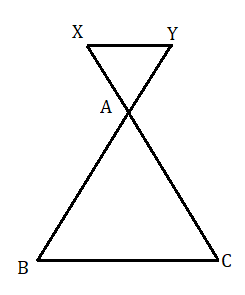
আবার নীচের চিত্রে XY সরলরেখা BA ও CA কে বহিঃর্বিভক্ত করেছে।
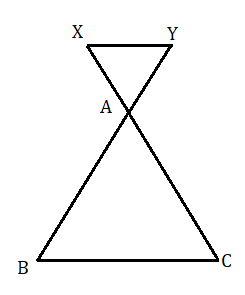
এক্ষেত্রেও
AX : XB = AY : YC
অর্থাৎ [tex]\frac{{AX}}{{XB}} = \frac{{AY}}{{YC}}[/tex]
XY সরলরেখা AB ও AC কে অন্তর্বিভক্ত করেছে এবং আমরা জানি [tex]\frac{{AX}}{{XB}} = \frac{{AY}}{{YC}}[/tex]
এ থেকে আমরা অনুপ্ৰে ধর্ম ব্যবহার করে আরো দুটো অনুসিদ্ধান্ত পাই।
(i) [tex]\frac{{AB}}{{XB}} = \frac{{AC}}{{YC}}[/tex]
(ii) [tex]\frac{{AB}}{{AX}} = \frac{{AC}}{{AY}}[/tex]
(i) যেহেতু [tex]\frac{{AX}}{{XB}} = \frac{{AY}}{{YC}}[/tex] অতএব
[tex]\begin{array}{l}
\frac{{AX}}{{XB}} + 1 = \frac{{AY}}{{YC}} + 1\\
\Rightarrow \frac{{AX + XB}}{{XB}} = \frac{{AY + YC}}{{YC}}\\
\Rightarrow \frac{{AB}}{{XB}} = \frac{{AC}}{{YC}}
\end{array}[/tex]
[tex]\begin{array}{l}
(ii)\frac{{AX}}{{XB}} = \frac{{AY}}{{YC}}\\
\Rightarrow \frac{{XB}}{{AX}} = \frac{{YC}}{{AY}}\\
\Rightarrow \frac{{XB}}{{AX}} + 1 = \frac{{YC}}{{AY}} + 1\\
\Rightarrow \frac{{XB + AX}}{{AX}} = \frac{{YC + AY}}{{AY}}\\
\Rightarrow \frac{{AB}}{{AX}} = \frac{{AC}}{{AY}}
\end{array}[/tex]
(৩) যে সরলরেখা কোনো ত্রিভুজের বাহু দুটিকে সমানুপাতে বিভক্ত করে তা তৃতীয় বাহুর সমান্তরাল হবে।
XY সরলরেখা ত্রিভুজ ABC এর AB ও AC বাহুটিকে যথাক্রমে X ও Y বিন্দুতে সমানুপাতে অন্তর্বিভক্ত করেছে।
অর্থাৎ [tex]\frac{{AX}}{{XB}} = \frac{{AY}}{{YC}}[/tex]
অর্থাৎ AX : XB = AY : YC
প্রতিজ্ঞা অনুযায়ী XY ।। BC হবে।
ডানপাশের চিত্রতে AB ও AC কে XY বহির্বিভক্ত করেছে। বামপাশের চিত্রতে BA ও CA কে XY বহির্বিভক্ত করেছে।
এখানে [tex]\frac{{AX}}{{XB}} = \frac{{AY}}{{YC}}[/tex]
অর্থাৎ AX : XB = AY : YC
প্রতিজ্ঞা অনুযায়ী XY ।। BC হবে।
কয়েকটি প্রয়োগ
(১) ABC ত্রিভুজের BC বাহুর সমান্তরাল সরলরেখা AB ও AC কে যথাক্রমে D ও E বিন্দুতে ছেদ করে। AE = 2AD হলে DB : EC নির্ণয় করো।
উত্তর : 
DE ।। BC .
অতএব
[tex]\begin{array}{l}
\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\\
\Rightarrow \frac{{AD}}{{AE}} = \frac{{DB}}{{EC}}
\end{array}[/tex]
কিন্তু [tex]AE = 2AD \Rightarrow \frac{{AD}}{{AE}} = \frac{1}{2}[/tex]
অতএব [tex]\frac{{DB}}{{EC}} = \frac{1}{2} \Rightarrow DB:EC = 1:2[/tex]
(২) ABCD ট্রাপিজিয়ামের AB ।। DC . AB এর সমান্তরাল একটি সরলরেখা AD ও BC কে যথাক্রমে E ও F বিন্দুতে ছেদ করে। প্রমাণ করতে হবে যে AE : ED =BF : FC .
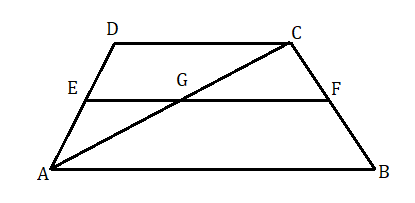অঙ্কন : A , C যুক্ত করা হল। AC , EF কে G বিন্দুতে ছেদ করেছে।
প্রমাণ : ত্রিভুজ ADC এর DC বাহুর সমান্তরাল সরলরেখা EG .
অতএব AE : ED = AG : GC
আবার ত্রিভুজ ABC এর AB বাহুর সমান্তরাল সরলরেখাস GF .
অতএব CF : FB = CG : GA .
অর্থাৎ AE : ED = AG : GC = FB : CF
বা , AE : ED = FB : CF
(৩) ABCD ট্রাপিজিয়ামের AB ।। DC . AD ও BC এর উপর যথাক্রমে P ও Q এমন দুটি বিন্দু নেওয়া হল যে AP : PD = BQ : QC .
প্রমাণ করতে হবে যে PQ ।। DC
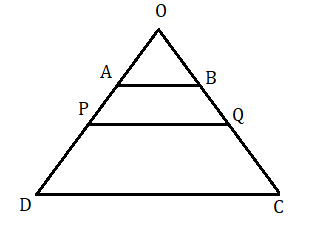অঙ্কন : মনে করি AB < DC . বর্ধিত DA ও CB পরস্পরকে O বিন্দুতে ছেদ করে। P , Q যুক্ত করা হল।
প্রমাণ : অতএব AB ।। DC .
ত্রিভুজ ODC থেকে পাওয়া যায়
[tex]\begin{array}{l}
OA:AD = OB:BC\\
\Rightarrow \frac{{OA}}{{AD}} = \frac{{OB}}{{BC}}
\end{array}[/tex]
আবার দেওয়া আছে
[tex]\begin{array}{l}
AP:PD = BQ:QC\\
\Rightarrow \frac{{AP}}{{PD}} = \frac{{BQ}}{{QC}}\\
\Rightarrow \frac{{PD}}{{AP}} = \frac{{QC}}{{BQ}}\\
\Rightarrow \frac{{PD}}{{AP}} + 1 = \frac{{QC}}{{BQ}} + 1\\
\Rightarrow \frac{{PD + AP}}{{AP}} = \frac{{QC + BQ}}{{BQ}}\\
\Rightarrow \frac{{AD}}{{AP}} = \frac{{BC}}{{BQ}}
\end{array}[/tex]
অতএব
[tex]\begin{array}{l}
\frac{{AD}}{{AP}} \times \frac{{OA}}{{AD}} = \frac{{BC}}{{BQ}} \times \frac{{OB}}{{BC}}\\
\Rightarrow \frac{{OA}}{{AP}} = \frac{{OB}}{{BQ}}
\end{array}[/tex]
অতএব ত্রিভুজ OPQ থেকে পাওয়া যায় AB ।। PQ
কিন্তু AB ।। DC অতএব PQ ।। DC
যেকোনো দুটি সদৃশকোণী ত্রিভুজের অনুরূপ বাহু গুলি সমানুপাতী , বিপরীতক্রমে বাহুগুলি সমানুপাতী হলে ত্রিভুজ দুটি সদৃশকোণী হবে।
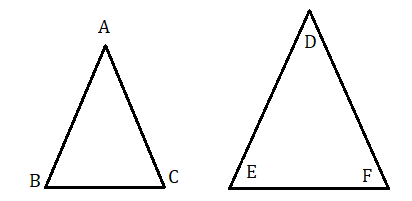
ত্রিভুজ ABC ও ত্রিভুজ DEF দুটি সদৃশকোণী ত্রিভুজের [tex]\angle A = \angle D,\angle B = \angle E,\angle C = \angle F[/tex]
অতএব প্রতিজ্ঞা অনুযায়ী [tex]\frac{{BC}}{{EF}} = \frac{{CA}}{{FD}} = \frac{{AB}}{{DE}}[/tex]
মন্তব্য : যেকোনো ত্রিভুজের কোনো বাহুর সমান্তরাল সরলরেখা অঙ্কন করার ফলে যে ত্রিভুজটি গঠিত হয় তা মূল ত্রিভুজের সঙ্গে সদৃশকোণী। সুতরাং তাদের অনুরূপ বাহুগুলি সমানুপাতী হবে।
কয়েকটি প্রয়োগ
(১) প্রমাণ করতে হবে যে ত্রিভুজের কোনো একটি বাহুর মধ্যবিন্দু দিয়ে অপর একটি বাহুর সমান্তরাল সরলরেখা অঙ্কন করলে তা তৃতীয় বাহুকে সমদ্বিখণ্ডিত করে এবং সেই সমান্তরাল সরলরেখাটি খন্ডিতাংশ দ্বিতীয় বাহুর অর্ধেক হবে।
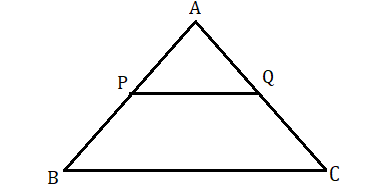মনে করি , ত্রিভুজ ABC এর AB বাহুর মধ্যবিন্দু P দিয়ে BC এর সমান্তরাল সরলরেখা অঙ্কন করা হল , যা AC কে Q বিন্দুতে ছেদ করে।
প্রমাণ করতে হবে (i) Q , AC এর মধ্যবিন্দু। (ii) [tex]PQ = \frac{1}{2}BC[/tex]
প্রমাণ : ত্রিভুজ APQ এবং ত্রিভুজ ABC এর
[tex]\angle PAQ = \angle BAC[/tex] ( একই কোণ )
[tex]\angle APQ = \angle ABC[/tex] ( অনুরূপ কোণ ) [ যেহেতু PQ ।। BC APB ভেদক .]
অতএব ত্রিভুজ APQ এবং ত্রিভুজ ABC সদৃশকোণী।
অতএব [tex]\frac{{AP}}{{AB}} = \frac{{AQ}}{{AC}} = \frac{{PQ}}{{BC}}[/tex]
কিন্তু [tex]\frac{{AP}}{{AB}} = \frac{1}{2}[/tex] ( যেহেতু P , AB এর মধ্যবিন্দু )
অতএব [tex]\frac{{AQ}}{{AC}} = \frac{1}{2}[/tex] . এর থেকে বোঝা যায় Q , AC এর মধ্যবিন্দু।
এবং[tex]\frac{{PQ}}{{BC}} = \frac{1}{2} \Rightarrow PQ = \frac{1}{2}BC[/tex]
(২) ত্রিভুজ ABC এর AD হল মধ্যমা। BC এর সমান্তরাল কোনো সরলরেখা AB ও AC কে যথাক্রমে P ও Q বিন্দুতে ছেদ করে। প্রমাণ করো যে ,AD দ্বারা PQ রেখাংশ সমদ্বিখণ্ডিত হবে।
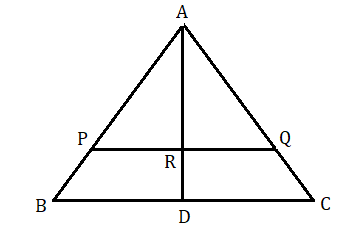মনে করি PQ , AD কে R বিন্দুতে ছেদ করেছে। আমাদের প্রমাণ করতে হবে যে PR = RQ .
প্রমাণ : ত্রিভুজ APR ও ত্রিভুজ ABD এর
[tex]\angle PAR = \angle BAD[/tex] ( একই কোণ )
[tex]\angle APR = \angle ABD[/tex] ( অনুরূপ কোণ ) [ যেহেতু PR ।। BD এবং AB ভেদক ]
অতএব ত্রিভুজ APR ও ত্রিভুজ ABD হল সদৃশকোণী
অতএব [tex]\frac{{PR}}{{BD}} = \frac{{AR}}{{AD}}[/tex]
অনুরূপভাবে প্রমাণ করা যায় [tex]\frac{{QR}}{{DC}} = \frac{{AR}}{{AD}}[/tex]
সুতরাং [tex]\frac{{PR}}{{BD}} = \frac{{QR}}{{DC}}[/tex]
কিন্তু BD = DC ( যেহেতু AD মধ্যমা )
অতএব PR = QR
(৩) ABCD একটি বৃত্তস্থ চতুর্ভুজ। বর্ধিত AB ও DC পরস্পরকে P বিন্দুতে ছেদ করে। প্রমাণ করো যে PA . PB = PC . PD
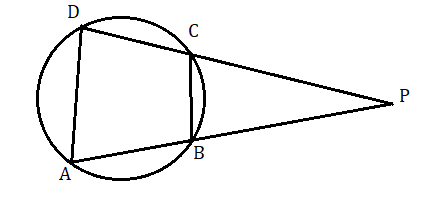প্রমাণ : ত্রিভুজ APD এবং ত্রিভুজ BPC এর
[tex]\angle APD = \angle BPC[/tex] ( একই কোণ )
[tex]\angle PAD = \angle PCB[/tex] ( যেহেতু ABCD একটি বৃত্তস্থ চতুর্ভুজ , সুতরাং [tex]\angle DAB + \angle DCB = {180^ \circ }[/tex] আবার [tex]\angle DCB + \angle BCP = {180^ \circ }[/tex])
অতএব ত্রিভুজ APD এবং ত্রিভুজ BPC হল সদৃশকোণী।
অতএব
[tex]\begin{array}{l}
\frac{{PA}}{{PC}} = \frac{{PD}}{{PB}}\\
\Rightarrow PA \cdot PB = PD \cdot PC
\end{array}[/tex]
মন্তব্য : PA . PB = PC . PD এই সম্পর্কটি যদি আমরা অনুপাতের সাহায্যে লিখি , তাহলে আমরা লিখতে পারি [tex]\frac{{PA}}{{PC}} = \frac{{PD}}{{PB}}[/tex] . এখন থেকেই বোঝা যাচ্ছে যে ত্রিভুজ APD এবং ত্রিভুজ BPC হল সদৃশকোণী।
কয়েকটি সদৃশ সমতলিক চিত্রের ধারণা
চিত্রের আকৃতি যদি একই হয় কিন্তু তাদের ক্ষেত্রফল বা আকার যদি আলাদা হয় সেই দুটি চিত্রকে সদৃশ বলা হয়। নীচে কয়েকটি চিত্র দেওয়া হল।
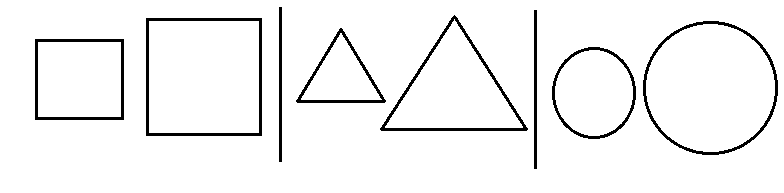
(i) সকল বর্গক্ষেত্র সদৃশ
(ii) সকল সমবাহু সদৃশ
(iii) সকল বৃত্ত সদৃশ
মনে রাখার বিষয়
(১) একটি বর্গক্ষেত্র ও একটি আয়তক্ষেত্র সদৃশকোণী কিন্তু তাদের অনুরূপ বাহুগুলি কখনোই সমানুপাতী হবেনা। কাজেই তারা সদৃশ নয়।
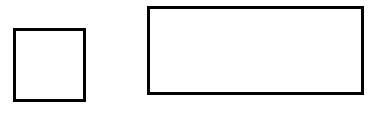
(২) একটি বর্গক্ষেত্র ও একটি রম্বসের অনুরূপ বাহুগুলি সর্বদাই সমানুপাতী হবে কিন্তু তারা কখনোই সদৃশকোণী হবেনা। কারণ বর্গক্ষেত্রের প্রত্যেকটি কোণ সমকোণ কিন্তু রম্বসের একটিও কোণ সমকোণ নয়। কাজেই ের সদৃশ নয়। দুটি ক্ষেত্রেই চতুর্ভুজ দুটির আকৃতি আলাদা।
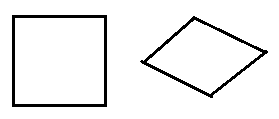
(৩) একই আকৃতির দুটি চতুর্ভুজ , যেমন দুটি আয়তক্ষেত্র যদি নেওয়া হয় তাহলে তারা সদৃশকোণী হলেও সদৃশ নাও হতে পারে।
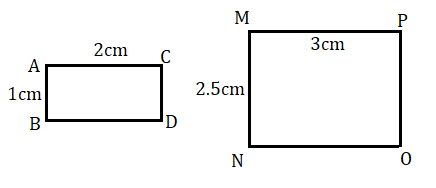
এখানে ABCD একটি আয়তক্ষেত্র যার AC = BD = 2cm এবং AB = CD = 1cm . আবার MNOP আর একটি আয়তক্ষেত্র যার MN = OP = 2.5cm এবং MP = NO = 3cm.তাহলে দেখা যাচ্ছে ের সদৃশকোণী হলেও অনুরূপ বাহুগুলি সমানুপাতী নয়। সুতরাং এরা সদৃশ নয়।
(৪) ত্রিভুজের ক্ষেত্রে বলতে পারি দুটি ত্রিভুজ সদৃশকোণী হলে ত্রিভুজ দুটি সদৃশ হবে। অথবা দুটি ত্রিভুজের বাহুগুলি সমানুপাতি হলে ত্রিভুজ দুটি সদৃশ হবে।
যেকোনো সমকোণী ত্রিভুজের সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে , ওই লম্বের উভয় পাশের ত্রিভুজদ্বয় পরস্পর সদৃশ হবে এবং ওই ত্রিভুজ গুলির প্রত্যেকে মূল ত্রিভুজের সঙ্গে সদৃশ।
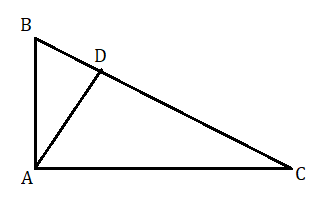দেওয়া আছে ABC একটি সমকোণী ত্রিভুজ যার [tex]\angle A[/tex] হল সমকোণ এবং A হল সমকৌণিক বিন্দু। AD হল সমকৌণিক বিন্দু A থেকে অতিভুজ BC এর উপর লম্ব।
প্রমাণ করতে হবে যে
- ত্রিভুজ DBA ও ত্রিভুজ ABC পরস্পর সদৃশ
- ত্রিভুজ DAC ও ত্রিভুজ ABC পরস্পর সদৃশ
- ত্রিভুজ DBA ও ত্রিভুজ DAC পরস্পর সদৃশ
প্রমাণ : [tex]\angle BDA = \angle BAC = \angle ADC = {90^ \circ }[/tex]
অতএব [tex]\angle BAD = \angle BCA = \angle ACD[/tex] ( [tex]\angle ABC[/tex] বা [tex]\angle ABD[/tex] এর পূরক কোণ )
এবং [tex]\angle ABD = \angle CBA = \angle CAD[/tex] ( [tex]\angle ACB[/tex] বা [tex]\angle ACD[/tex] এর পূরক কোণ )
প্রথম ও দ্বিতীয় সম্পর্ক থেকে আমরা পাই ত্রিভুজ DBA ও ত্রিভুজ ABC সদৃশকোণী।
অতএব ত্রিভুজ DBA ও ত্রিভুজ ABC পরস্পর সদৃশ।
দ্বিতীয় ও তৃতীয় সম্পর্ক থেকে আমরা পাই ত্রিভুজ ABC ও ত্রিভুজ DAC সদৃশকোণী।
অতএব ত্রিভুজ ABC ও ত্রিভুজ DAC পরস্পর সদৃশ।
এবং প্রথম ও তৃতীয় সম্পর্ক থেকে পাই ত্রিভুজ DBA ও ত্রিভুজ DAC সদৃশকোণী।
অতএব ত্রিভুজ DBA ও ত্রিভুজ DAC পরস্পর সদৃশ।
অনুসিদ্ধান্ত :
(১) পাশের চিত্র থেকে দেখা যাচ্ছে
(i) [tex]A{B^2} = BC \cdot BD[/tex]
(ii) [tex]A{D^2} = BD \cdot CD[/tex]
(iii) [tex]A{C^2} = BC \cdot CD[/tex]
(i) ত্রিভুজ DBA ও ত্রিভুজ ABC সদৃশকোণী।
অতএব [tex]\frac{{AB}}{{BC}} = \frac{{BD}}{{AB}} \Rightarrow A{B^2} = BC \cdot BD[/tex]
(ii) ত্রিভুজ DBA ও ত্রিভুজ DAC সদৃশকোণী।
অতএব [tex]\frac{{AD}}{{CD}} = \frac{{BD}}{{AD}} \Rightarrow A{D^2} = BD \cdot CD[/tex]
(iii) ত্রিভুজ ABC ও ত্রিভুজ DAC সদৃশকোণী।
অতএব [tex]\frac{{AC}}{{BC}} = \frac{{CD}}{{AC}} \Rightarrow A{C^2} = BC \cdot CD[/tex]
(২) অনুসিদ্ধান্ত থেকে আমরা দেখতে পাচ্ছি AB , AD ও AC যথাক্রমে BC , BD ; BD , CD ও BC , CD এর সমানুপাতী। অর্থাৎ AB , AD ও AC বাহুবিশিষ্ট বর্গক্ষেত্রের ক্ষেত্রফল যথাক্রমে BC ও BD বাহুবিশিষ্ট আয়তক্ষেত্র , BD ও CD বাহুবিশিষ্ট আয়তক্ষেত্র এবং BC ও CD বাহুবিশিষ্ট আয়তক্ষেত্রের ক্ষেত্রফলের সঙ্গে সমান হবে।
(৩) যেকোনো দুটি সমকোণী ত্রিভুজের একটি করে সূক্ষকোণ যদি সমান হয় , তাহলে অপর সূক্ষকোণ দুটিও সমান হবে অর্থাৎ ত্রিভুজ দুটি সদৃশকোণী হবে। সুতরাং এই ত্রিভুজের দুটি অনুরূপ বাহু গুলি সমানুপাতী হবে।
কয়েকটি প্রয়োগ
(১) যদি কোনো সমকোণী ত্রিভুজ ABC এর সমকৌণিক বিন্দু A থেকে অতিভুজের উপরে লম্ব টানা যায় এবং যদি AC , AB , BC ক্রমিক সমানুপাতী হয় তবে অতিভুজের বৃহত্তম অংশ ত্রিভুজটির ক্ষুদ্রত্তম বাহুর সমান হয়।
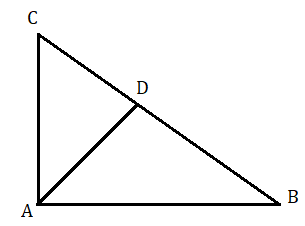ABC সমকোণী ত্রিভুজের [tex]\angle A[/tex] হল সমকোণ। A থেকে অতিভুজ BC এর উপর AD লম্ব টানা হল। মনে করি AC ক্ষুদ্রত্তম বাহু। দেওয়া আছে [tex]AC:AB = AB:BC \Rightarrow \frac{{AC}}{{AB}} = \frac{{AB}}{{BC}}[/tex] . আবার ADC সমকোণী ত্রিভুজের DC , অতিভুজ AC এর সমান হতে পারে না। কাজেই প্রমাণ করতে হবে BD = AC .
প্রমাণ : সমকোণ A থেকে অতিভুজ BC এর উপর AD লম্ব।
অতএব ত্রিভুজ ABD ও ত্রিভুজ ABC সদৃশ।
অতএব [tex]\frac{{BD}}{{AB}} = \frac{{AB}}{{BC}} \Rightarrow A{B^2} = BD \cdot BC[/tex]
এখন
[tex]\begin{array}{l}
\frac{{AC}}{{AB}} = \frac{{AB}}{{BC}}\\
\Rightarrow A{B^2} = AC \cdot BC\\
\Rightarrow BD \cdot BC = AC \cdot BC\\
\Rightarrow BD = AC
\end{array}[/tex]
(২) কোনো বৃত্তের AB একটি ব্যাস। বৃত্তের উপরে অবস্থিত কোনো বিন্দু P থেকে AB এর উপর অঙ্কিত লম্ব AB কে N বিন্দুতে ছেদ করে। প্রমাণ করতে হবে যে [tex]P{B^2} = AB \cdot BN[/tex]
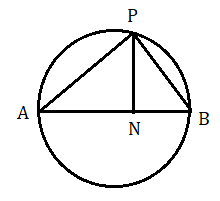প্রমাণ : AB ব্যাস অতএব [tex]\angle APB[/tex] হল অর্ধবৃত্তস্থ কোণ।
সুতরাং [tex]\angle APB = {90^ \circ }[/tex]
সমকোণী ত্রিভুজের APB এর সমকৌণিক বিন্দু P থেকে অতিভুজ AB এর উপর PN লম্ব। অতএব ত্রিভুজ APB ও ত্রিভুজ PBN পরস্পর সদৃশ।
অতএব
[tex]\begin{array}{l}
\frac{{PB}}{{AB}} = \frac{{BN}}{{PB}}\\
\Rightarrow P{B^2} = AB \cdot BN
\end{array}[/tex]
(৩) দুটি বৃত্ত পরস্পরকে A বিন্দুতে বহিঃস্পর্শ করেছে। PQ ওই দুটি বৃত্তের একটি সরল সাধারণ স্পর্শক। যদি বৃত্ত দুটির ব্যাসার্ধ যথাক্রমে r ও r' হয় , তাহলে প্রমাণ করো যে [tex]P{Q^2} = 4rr'[/tex]
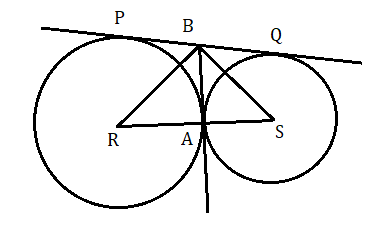মনে করি একটি বৃত্তের কেন্দ্র হল R এবং ওপর বৃত্তটির কেন্দ্র হল S . আরো ধরা যাক R বৃত্তের ব্যাসার্ধ হল r এবং S বৃত্তের ব্যাসার্ধ হল r' .
অঙ্কন : R , A এবং S যুক্ত করা হল। A বিন্দুতে বৃত্ত দুটির সাধারণ স্পর্শক অঙ্কন করা হল , যা PQ কে B বিন্দুতে ছেদ করে। B , R এবং B , S যুক্ত করা হল।
প্রমাণ : B বিন্দু থেকে R কেন্দ্রীয় বৃত্তে BP এবং BA দুটি স্পর্শক।
অতএব BP = BA এবং BR , [tex]\angle ABP[/tex] এর সমদ্বিখণ্ডক।
অনুরূপভাবে BQ = AB এবং BS , [tex]\angle ABQ[/tex] এর সমদ্বিখণ্ডক।
অতএব
[tex]\begin{array}{l}
\angle RBS = {180^ \circ } - \left( {\angle PBR + \angle QBS} \right) = {180^ \circ } - \angle RBS\\
\Rightarrow 2\angle RBS = {180^ \circ }\\
\Rightarrow \angle RBS = {90^ \circ }
\end{array}[/tex]
অতএব R , S দুটি বৃত্তের কেন্দ্র , A স্পর্শবিন্দু।
অতএব R , A এবং S হল সমরেখ এবং \[AB \bot RS\]
সমকোণী ত্রিভুজ RBS এর সমকৌণিক বিন্দু B থেকে BA অতিভুজ RS এর উপর লম্ব।
অতএব ত্রিভুজ ABR ও ত্রিভুজ ASB সদৃশ।
অতএব
[tex]\begin{array}{l}
\frac{{AB}}{{AS}} = \frac{{AR}}{{AB}}\\
\Rightarrow A{B^2} = AR \cdot AS\\
\Rightarrow A{B^2} = r \cdot r'\\
\Rightarrow 4A{B^2} = 4r \cdot r'\\
\Rightarrow {\left( {2AB} \right)^2} = 4r \cdot r'\\
\Rightarrow P{Q^2} = 4r \cdot r'
\end{array}[/tex]
( যেহেতু PQ = PB + BQ = 2AB )
পিথাগোরাস উপপাদ্য : যেকোনো সমকোণী ত্রিভুজের অতিভুজের উপর বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর উপর বর্গক্ষেত্রের ক্ষেত্রফলের সমষ্টির সমান হবে।
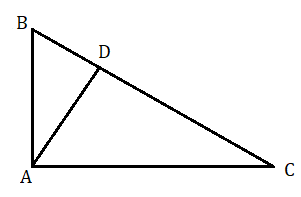
মনে করি ABC একটি সমকোণী ত্রিভুজ যার [tex]\angle A[/tex] হল সমকোণ।
আমাদের প্রমাণ করতে হবে যে [tex]B{C^2} = A{B^2} + A{C^2}[/tex]
অঙ্কন : সমকৌণিক বিন্দু A থেকে অতিভুজ BC এর উপরে AD লম্ব টানা হল।
প্রমাণ : সমকোণী ত্রিভুজ ABC এর অতিভুজ BC এর উপর AD
অতএব ত্রিভুজ ABD ও ত্রিভুজ CBA সদৃশ
অতএব [tex]\frac{{AB}}{{BC}} = \frac{{BD}}{{AB}} \Rightarrow A{B^2} = BC \cdot BD[/tex]
আবার ত্রিভুজ ACD ও ত্রিভুজ CBA সদৃশ
অতএব [tex]\frac{{AC}}{{BC}} = \frac{{DC}}{{AC}} \Rightarrow A{C^2} = DC \cdot BC[/tex]
এখন
[tex]\begin{array}{l}
A{B^2} + A{C^2}\\
= BC \cdot BD + DC \cdot BC\\
= BC \cdot \left( {BD + DC} \right)\\
= BC \cdot BC = B{C^2}\\
\Rightarrow B{C^2} = A{B^2} + A{C^2}
\end{array}[/tex]
পিথাগোরাস উপপাদ্যের বিপরীত উপপাদ্য :
যেকোনো ত্রিভুজের এক বাহুর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টির সমান হলে ঐ দুই বাহু দ্বারা উৎপন্ন কোণটি সমকোণ হবে।
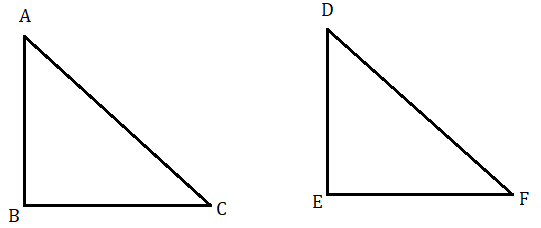
ABC ত্রিভুজের AB এর উপর অঙ্কিত বর্গক্ষেত্র , BC ও AC বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের সমষ্টির সমান অর্থাৎ [tex]A{C^2} = A{B^2} + B{C^2}[/tex] . প্রমাণ করতে হবে যে , [tex]\angle ABC = {90^ \circ }[/tex] .
অঙ্কন : BC এর সমান করে EF সরলরেখা টানা হল।
AB এর সমান করে EF এর উপর ED লম্ব টানা হল। DF যোগ করা হল।
প্রমাণ :
[tex]\begin{array}{l}
A{C^2} = A{B^2} + B{C^2}\\
= D{E^2} + E{F^2}\\
= D{F^2}\\
\Rightarrow AC = DF
\end{array}[/tex]
এখন ত্রিভুজ ABC ও ত্রিভুজ DEF এর AB = DE , BC = EF এবং AC = DF .
অতএব ত্রিভুজদ্বয় সর্বসম।
অতএব [tex]\angle ABC = \angle DEF[/tex]
কিন্তু [tex]\angle DEF = {90^ \circ }[/tex] . অতএব [tex]\angle ABC = {90^ \circ }[/tex] .
সমকোণী ত্রিভুজ নির্ণয়ের সাধারণ সূত্র
এই প্রতিজ্ঞা হতে কোনো ত্রিভুজ সমকোণী কিনা সহজে বোঝা যায়। যদি প্রদত্ত বাহুগুলির দৈর্ঘ্য এমন হয় যে , একটির বর্গ অপর দুটির বর্গের সমষ্টি সমান , তবে ত্রিভুজটি সমকোণী হবে।
কয়েকটি প্রয়োগ
(১) কোনো বর্গক্ষেত্রে এর ক্ষেত্রফল কর্ণের উপর অঙ্কিত বর্গক্ষেত্র ঐ বর্গক্ষেত্রের ক্ষেত্রফলের দ্বিগুন।
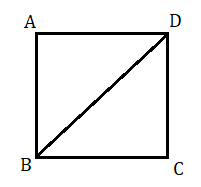ধরা যাক , ABCD একটি বর্গক্ষেত্র এবং BD একটি কর্ণ। প্রমাণ করতে হবে যে , [tex]B{D^2} = 2B{C^2}[/tex]
প্রমাণ : অতএব ABCD একটি বর্গক্ষেত্র ,
অতএব BCD সমকোণী ত্রিভুজ এবং BC = CD .
অতএব [tex]B{D^2} = B{C^2} + C{D^2} = 2B{C^2}[/tex]
(২) ABCD একটি আয়তক্ষেত্র এবং O আয়তক্ষেত্রের অভ্যন্তরে যেকোনো একটি বিন্দু। প্রমাণ করো যে , [tex]O{A^2} + O{C^2} = O{B^2} + O{D^2}[/tex]
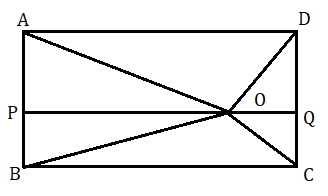অঙ্কন : O বিন্দু দিয়ে BC এর সমান্তরাল অঙ্কন করা হল , যা AB ও DC কে যথাক্রমে P ও Q বিন্দুতে ছেদ করে।
প্রমাণ : যেহেতু BC ।। PQ
অতএব [tex]PQ \bot AB[/tex] . [tex]PQ \bot CD[/tex]
অতএব ত্রিভুজ APO , ত্রিভুজ BPO , ত্রিভুজ DQO এবং ত্রিভুজ CQO এরা প্রত্যেকেই সমকোণী ত্রিভুজ।
অতএব [tex]O{A^2} = A{P^2} + P{O^2}[/tex]
[tex]O{B^2} = P{O^2} + B{P^2}[/tex]
[tex]O{C^2} = O{Q^2} + Q{C^2}[/tex]
[tex]O{D^2} = O{Q^2} + Q{D^2}[/tex]
অতএব [tex]O{A^2} + O{C^2} = A{P^2} + P{O^2} + O{Q^2} + Q{C^2}[/tex]
কিন্তু অঙ্কন অনুসারে , APQD ও BPQC এরা প্রত্যেকেই আয়তক্ষেত্র।
অতএব AP = DQ এবং CQ = BP
অতএব
[tex]\begin{array}{l}
O{A^2} + O{C^2}\\
= A{P^2} + P{O^2} + O{Q^2} + Q{C^2}\\
= Q{D^2} + P{O^2} + O{Q^2} + B{P^2}\\
= O{Q^2} + Q{D^2} + P{O^2} + B{P^2}\\
= O{D^2} + O{B^2}
\end{array}[/tex]
(৩) ত্রিভুজ ABC একটি সমদ্বিবাহু ত্রিভুজ , যার [tex]\angle B[/tex] হল সমকোণ। [tex]\angle BAC[/tex] এর সমদ্বিখণ্ডক BC কে D বিন্দুতে ছেদ করে। প্রমাণ করো যে , [tex]C{D^2} = 2B{D^2}[/tex]
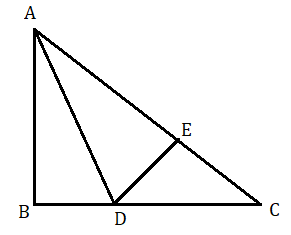অঙ্কন : D বিন্দু থেকে AC এর উপর DE লম্ব অঙ্কন করা হল।
প্রমাণ : ত্রিভুজ ABC হল সমকোণী সমদ্বিবাহু।
অতএব [tex]\angle ACB = {45^ \circ }[/tex]
অতএব ত্রিভুজ DEC সমকোণী সমদ্বিবাহু ত্রিভুজ।
আবার ত্রিভুজ ABD ও ত্রিভুজ AED এর
[tex]\angle BAD = \angle EAD[/tex]
[tex]\angle ABD = \angle AED[/tex] ( উভয়ই সমকোণ )
AD সাধারণ বাহু ( অনুরূপ বাহু )
অতএব ত্রিভুজ ABD [tex] \cong [/tex] ত্রিভুজ AED
অতএব BD = DE
এবার ত্রিভুজ DEC সমকোণী সমদ্বিবাহু ত্রিভুজ
অতএব [tex]D{C^2} = 2D{E^2} = 2B{D^2}[/tex]
(৪) ABC ত্রিভুজের [tex]\angle A[/tex] হল সমকোণ। BP ও CQ দুটি মধ্যমা। প্রমাণ করো যে [tex]5B{C^2} = 4\left( {B{P^2} + C{Q^2}} \right)[/tex]
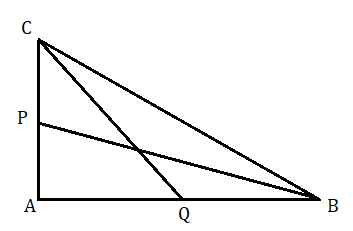প্রমাণ : ত্রিভুজ ABC এর [tex]\angle A[/tex] হল সমকোণ।
অতএব [tex]B{C^2} = A{B^2} + A{C^2}[/tex]
যেহেতু P এবং Q যথাক্রমে AC ও AB এর মধ্যবিন্দু।
অতএব
[tex]\begin{array}{l}
B{C^2}\\
= A{B^2} + A{C^2}\\
= {\left( {2AQ} \right)^2} + {\left( {2AP} \right)^2}\\
= 4\left( {A{Q^2} + A{P^2}} \right)
\end{array}[/tex]
আবার ত্রিভুজ BAP , ত্রিভুজ CAQ সমকোণী ত্রিভুজ ,
অতএব
[tex]\begin{array}{l}
B{P^2}\\
= A{B^2} + A{P^2}\\
= {\left( {2AQ} \right)^2} + A{P^2}\\
= 4A{Q^2} + A{P^2}
\end{array}[/tex]
এবং
[tex]\begin{array}{l}
C{Q^2}\\
= A{C^2} + A{Q^2}\\
= {\left( {2AP} \right)^2} + A{Q^2}\\
= 4A{P^2} + A{Q^2}
\end{array}[/tex]
অতএব
[tex]\begin{array}{l}
B{P^2} + C{Q^2}\\
= 4A{Q^2} + A{P^2} + 4A{P^2} + A{Q^2}\\
= 4\left( {A{Q^2} + A{P^2}} \right) + A{Q^2} + A{P^2}\\
= 5\left( {A{Q^2} + A{P^2}} \right)
\end{array}[/tex]
অতএব
[tex]\begin{array}{l}
5B{C^2} = 5 \cdot 4\left( {A{Q^2} + A{P^2}} \right)\\
\Rightarrow 5B{C^2} = 4\left( {B{P^2} + C{Q^2}} \right)
\end{array}[/tex]
- 21839 views
