লম্ব প্রিজম (Right Prism)
সূচনা (Introduction) :- আয়তঘন ও ঘনকের তল আয়তন (ঘনফল) পরিমাপ সম্মন্ধে এর আগে আমরা জেনেছি । এই অধ্যায়ে প্রিজম ঘন বস্তুটি সম্পর্কে আমরা আলোচনা করব ।
প্রিজম সম্পর্কে আলোচনা করার আগে আমাদের বহুতল সম্পর্কে আলোচনা করা দরকার । কয়েকটি সমতল দ্বারা সীমাবদ্ধ বস্তুকে বহুতলক (Polyhedron) বলে । সমতলগুলিকে বহুতলটির তল (Surface or face) বলা হয় । দুটি তল যে সরলরেখায় ছেদ করে তাকে প্রান্তিকী বা প্রান্তরেখা (Edge) বলা হয় । প্রান্তিকী গুলি যে বিন্দুতে মিলিত হয় শীর্ষ (Vertex) বলা হয় । ভিন্ন তলে অবস্থিত এমন দুটি শীর্ষের সংযোগ রেখাকে বলা হয় কর্ণ (Diagonal) বলে ।
প্রিজমের সংজ্ঞা (Defination of Prism) :- কোনো বহুতলকের র্শ্বতল (Side face) গুলি সামান্তরিক এবং প্রান্ততল (End face) দুটি সমান্তরাল ও সর্বসম হলে তাকে প্রিজম (Prism) বলে । দুটি পার্শ্বতলের ছেদ রেখাকে পার্শ্বপ্রান্তিকী (Side edge) বলা হয় । যে প্রিজমের পার্শ্বতল গুলি আয়তক্ষেত্র তাকে লম্ব প্রিজম (Right Prism) বলে । অন্যথায় তির্যক প্রিজম বলে । এর পরে আমরা লম্ব প্রিজম সম্মন্ধে আলোচনা করব । লম্ব প্রিজমের পার্শ্বপ্রান্তিকীকে প্রিজমের উচ্চতা (Height) বলে । ওই পার্শ্বপ্রান্তিকী প্রান্ততলদ্বয়ের সংলগ্ন বহু দুটির উপরে লম্ব হয় । প্রান্ততল দুটির মধ্যে যে প্রান্ততলের উপরে প্রিজমটি দন্ডায়মান থাকে তাকে প্রিজমের ভূমি (Base) বলে । যেকোনো প্রান্ততলকে ভূমি ধরা হয় । প্রিজমের ভূমি ত্রিভুজ, চতুর্ভুজ ইত্যাদি হলে প্রিজমটিকে যথাক্রমে ত্রিভুজাকার প্রিজম, চতুর্ভুজাকার প্রিজম বলে । আয়তঘন হল আয়তকার ভূমি বিশিষ্ট প্রিজম । বর্গাকার ভূমি বিশিষ্ট কোনো প্রিজমের উচ্চতা ভূমির বাহুর সমান হলে প্রিজমটি ঘনক হয় । প্রিজমের বাহুর সংখ্যা n হলে প্রিজমের পার্শ্বতলের সংখ্যা n পার্শ্বপ্রান্তিকীর সংখ্যা n , সমগ্র তলের সংখ্যা n + 2 , সমগ্র প্রান্তিকীর সংখ্যা 3n এবং শীর্ষের সংখ্যা 2n হয় ।
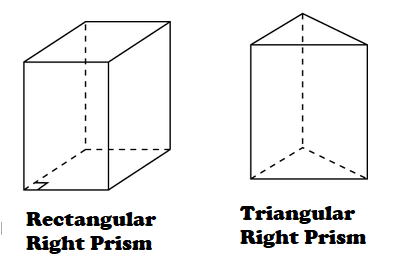
প্রিজমের তল ও আয়তন পরিমাপ সংক্রান্ত সূত্রাবলি :
1. পার্শ্বতলসমূহের ক্ষেত্রফল =(ভূমির পরিসীমা × উচ্চতা) বর্গ একক
2. সমগ্রতলের ক্ষেত্রফল = (পার্শ্বতলগুলির ক্ষেত্রফল + 2 × ভূমির ক্ষেত্রফল) বর্গ একক
3. আয়তন বা ঘনফল = (ভূমির ক্ষেত্রফল × উচ্চতা) ঘন একক
উদাহরণ 1. একটি প্রিজমের ভূমি 6 সেমি , 8 সেমি ও 10 সেমি বাহুবিশিষ্ট ত্রিভুজ এবং উচ্চতা 5 সেমি । প্রিজমটির সমগ্র তলের ক্ষেত্রফল ও আয়তন নির্ণয় করো ।
সমাধান : ভূমির পরিসীমা = ( 6 + 8 + 10 ) সেমি = 24 সেমি
অর্ধ পরিসীমা = ( 24÷2 ) সেমি = 12 সেমি
ভূমির ক্ষেত্রফল
= √12(12−6)(12−8)(12−10) বর্গসেমি
= √12×6×4×2 বর্গসেমি
= 4×2×3 বর্গসেমি
= 24 বর্গসেমি
পার্শ্বতলসমূহের ক্ষেত্রফল
= (ভূমির পরিসীমা × উচ্চতা) বর্গ একক
= (24 × 5) বর্গসেমি
= 120 বর্গসেমি।
সমগ্রতলের ক্ষেত্রফল
= (পার্শ্বতলগুলির ক্ষেত্রফল + 2 × ভূমির ক্ষেত্রফল) বর্গ একক
= (120 + 2 × 24) বর্গসেমি
= (120 + 48) বর্গসেমি
= 168 বর্গসেমি
আয়তন
= (ভূমির ক্ষেত্রফল × উচ্চতা) ঘন একক
= (24 × 5) ঘনসেমি
= 120 ঘনসেমি
- 6570 views