বৃত্ত সংক্রান্ত উপপাদ্য ( Theorems related to circle )
সূচনা (Introduction)
আমরা এর আগে বৃত্তের সঙ্গে পরিচিত হয়েছি এবং বৃত্ত সম্পর্কিত বৃত্তের সংজ্ঞা , বৃত্তের কেন্দ্র , বৃত্তের ব্যাসার্ধ , বৃত্তের ব্যাস , বৃত্তচাপ ,বৃত্তের জ্যা এবং অৰ্ধবৃত্ত এর গুলোর সঙ্গে আমাদের পরিচয় ঘটেছে। এই অধ্যায়ে বৃত্ত সম্বন্ধীয় প্রতিপাদ্য আলোচনা করা হবে , তার জন্য প্রয়োজনীয় বিষয় গুলি আর একবার আলোচনা করব।
বৃত্তাংশ : কোনো বৃত্তের একটি জ্যা ও একটি চাপের দ্বারা গঠিত চিত্রকে বলা হয় বৃত্তাংশ।
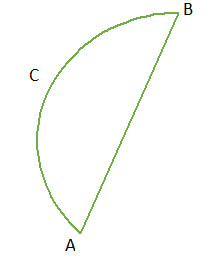
উপরের চিত্রে ACB একটি বৃত্তাংশ যা AB জ্যা এবং ACB বৃত্তচাপ গঠিত।
বৃত্তকলা : কোনো বৃত্তের দুটি ব্যাসার্ধ ও একটি চাপ দ্বারা গঠিত চিত্রকে বলা হয় বৃত্তকলা।
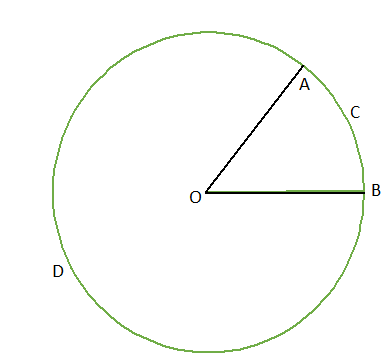
উপরের চিত্রে যেমন OA এবং OB দুটি ব্যাসার্ধ ও একটি বৃত্তচাপ ACB দ্বারা গঠিত OACB একটি বৃত্তকলা। অনুরূপে OADB আর একটি বৃত্তকলা , যা ব্যাসার্ধ OA এবং OB ও বৃত্তচাপ ADB দ্বারা গঠিত।
এককেন্দ্রীয় বৃত্তসমূহ : একটি বৃত্তকে কেন্দ্র করে একাধিক বৃত্ত অঙ্কন করা হলে , ওই বৃত্ত গুলিকে বলা হয় এককেন্দ্রীয় বৃত্তসমূহ।
বিভিন্ন সংখ্যক বিন্দুগামী বৃত্ত আঁকার সম্ভাব্যতা
আমরা জানি একটি বৃত্ত অঙ্কন করতে হলে প্রয়োজন একটি কেন্দ্র এবং একটি ব্যাসার্ধ। যদি কেন্দ্র ও ব্যাসার্ধ নির্দিষ্ট না বলা থাকে তাহলে আমরা অসংখ্য বৃত্ত অঙ্কন করতে পারি। কেন্দ্র নির্দিষ্ট এবং ব্যাসার্ধ নির্দিষ্ট না থাকলে আমরা অসংখ্য বৃত্ত অঙ্কন করতে পারি এবং সেগুলি হবে এককেন্দ্রীয় বৃত্ত। আবার ব্যাসার্ধ নির্দিষ্ট কিন্তু কেন্দ্র পৃথক পৃথক হলে যে সব বৃত্ত গুলি অঙ্কন করতে পারি তারা হবে তারা হবে সর্বসম।
আবার দেখা যায় একটি বিন্দু দিয়ে অসংখ্য বৃত্ত অঙ্কন করা যায়।
যদি দুটি নির্দিষ্ট বিন্দুগামী বৃত্ত অঙ্কন করতে হয় তাহলে কতগুলি বৃত্ত পাবো ? সেক্ষেত্রে দেখা যায় অসংখ্য বৃত্ত পাওয়া যায়। ধরা যাক A ও B দুটি নির্দিষ্ট বিন্দু। তাহলে বৃত্ত গুলির কেন্দ্র এমন স্থানে অবস্থিত হতে হবে যে তার থেকে A ও B সমদূরতে অবস্থিত হবে।
ধরা যাক A ও B দুটি নির্দিষ্ট বিন্দু। তাহলে বৃত্ত গুলির কেন্দ্র এমন নির্দিষ্ট স্থানে
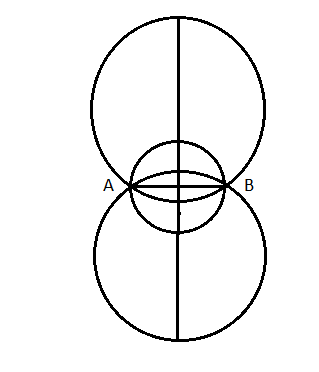
অবস্থিত হতে হবে যে তা থেকে A ও B যেন সমদূরত্বে থাকে। আমরা পূর্বে দেখেছি যে AB রেখাংশের লম্ব সমদ্বিখণ্ডকের উপরে অবস্থিত যেকোনো বিন্দুকে কেন্দ্র করে ওই বিন্দু ও A অথবা B বিন্দুর সংযোগ রেখাংশকে ব্যাসার্ধ নিয়ে বৃত্ত অঙ্কন করলেই তা A এবং B বিন্দুগামী হবে।
এবার দেখা যাক তিনটি নির্দিষ্ট বিন্দু দিয়ে কতগুলি বৃত্ত অঙ্কন করা যাবে। প্রথমে দেখি বিন্দুগুলি যদি অসমরেখ হয় তাহলে কি হবে ?
তিনটি অসমরেখ বিন্দু দিয়ে বৃত্ত অঙ্কন করতে হলে প্রথমেই আমাদের অন্তত একটি বিন্দু খুঁজে বের করতে হবে , যার থেকে ওই তিনটি বিন্দুর দূরত্ব সমান হয়।
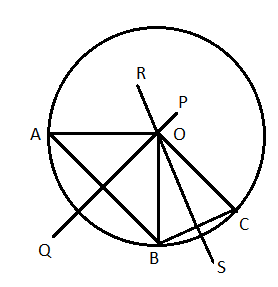
মনে করি প্রদত্ত বিন্দু তিনটি হল A , B এবং C . তবে AB এর লম্ব সমদ্বিখণ্ডক PQ এর উপর অবস্থিত আবার B ও C থেকে সমদূরবর্তী বিন্দু BC এর লম্ব সমদ্বিখণ্ডক RS এর উপর অবস্থিত। যেহেতু A , B ও C তিনটি অসমরেখ বিন্দু তাই AB ও BC এর লম্ব সমদ্বিখণ্ডক অর্থাৎ PQ এবং RS একটি নির্দিষ্ট বিন্দু O তে পরস্পরকে ছেদ করবে। অতএব O বিন্দুকে কেন্দ্র করে A , B ও C বিন্দু দিয়ে একটি মাত্র বৃত্ত অঙ্কন করা যাবে।
সুতরাং আমরা সিদ্ধান্ত নিতে পারি তিনটি অসমরেখ বিন্দু দিয়ে একটি মাত্র বৃত্ত অঙ্কন করা যায়। অপরপক্ষে তিনটি বিন্দু সমরেখ হলে বৃত্ত অঙ্কন করা সম্ভব নয়।
মন্তব্য :
- একটি বিন্দু দিয়ে অসংখ্য বৃত্ত অঙ্কন করা যায়।
- দুটি বিন্দু দিয়ে অসংখ্য বৃত্ত অঙ্কন করা যায়।
- তিনটি অসমরেখ বিন্দু দিয়ে একটি মাত্র বৃত্ত অঙ্কন করা যায়।
- তিনটির বেশি বিন্দু দিয়ে একটি বৃত্ত অঙ্কন করা সম্ভব নাও হতে পারে। যদি সম্ভব হয় তাদের সমবৃত্তস্থ বিন্দু বলা হয়।
- যে চতুর্ভুজের শীর্ষবিন্দু গুলি কোনো বৃত্তের উপর অবস্থিত হয় , সেই চতুর্ভুজকে বৃত্তস্থ চতুর্ভুজ বলা হয়।
বিশেষ ধর্ম
 (১) একটি সমদ্বিবাহু শীর্ষবিন্দু গুলি সমবৃত্তস্থ।
(১) একটি সমদ্বিবাহু শীর্ষবিন্দু গুলি সমবৃত্তস্থ।
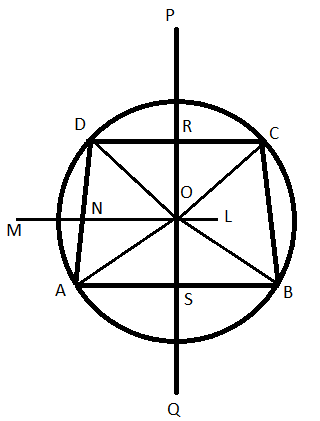
ABCD একটি সমদ্বিবাহু ট্রাপিজিয়াম , যার AB এবং DC বাহু পরস্পর সমান্তরাল এবং তির্যক বাহুদ্বয় সমান , অর্থাৎ DA = BC .আমাদের প্রমাণ করতে হবে যে ABCD সমবৃত্তস্থ ।
অঙ্কন : DC বাহুর লম্বসমদ্বিখণ্ডক PQ অঙ্কন করা হল। ওই লম্বসমদ্বিখণ্ডক AB বাহুরও লম্বসমদ্বিখণ্ডক হবে।
মনে করি PQ , DC ও AB কে যথাক্রমে R ও S বিন্দুতে ছেদ করেছে ।
AD এর লম্বসমদ্বিখণ্ডক LM অঙ্কন করা হল, যা PQ কে O বিন্দুতে ও AD কে N বিন্দুতে ছেদ করেছে ।
O বিন্দুর সঙ্গে যথাক্রমে A , B , C , D বিন্দুগুলিকে যুক্ত করা হল ।
প্রমাণ : আমরা বলতে পারি O , DC এর লম্বসমদ্বিখণ্ডকের উপরে অবস্থিত ।
অতএব OC = OD .
অনুরূপভাবে OD =OA OA =OB .
অতএব O কে কেন্দ্র করে OC ব্যাসার্ধ নিয়ে যে বৃত্ত অঙ্কন করা হবে , তা D , A , B বিন্দু দিয়েও যাবে , অর্থাৎ A , B , C , D সমবৃত্তস্থ ।
(২) ব্যাস নয় এইরূপ কোনো জ্যা কে যদি বৃত্তের কেন্দ্রগামী কোনো সরলরেখা সমদ্বিখণ্ডিত করে , তাহলে ওই সরলরেখা জ্যা এর উপর লম্ব হবে ।
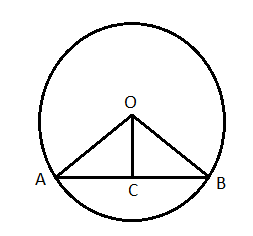 ধরা যাক O হল বৃত্তের কেন্দ্র , AB হল তার একটি জ্যা। OC সরলরেখাটি AB কে সমদ্বিখণ্ডিত করেছে । আমাদের প্রমাণ করতে হবে যে OC , AB উপর লম্ব ।
ধরা যাক O হল বৃত্তের কেন্দ্র , AB হল তার একটি জ্যা। OC সরলরেখাটি AB কে সমদ্বিখণ্ডিত করেছে । আমাদের প্রমাণ করতে হবে যে OC , AB উপর লম্ব ।
অঙ্কন : O , A এবং O , B যুক্ত করা হল ।
প্রমাণ : Δ OAC ও Δ OBC এর
OA = OB (O কেন্দ্রীয় বৃত্তের ব্যাসার্ধ)
OC সাধারণ বাহু ।
AC = BC ( OC , AB কে সমদ্বিখণ্ডিত করেছে )
অতএব Δ OAC ও Δ OBC হল সর্বসম।
সুতরাং আমরা বলতে পারি [tex]\angle OCA = \angle OCB[/tex]
অতএব OC , AB এর উপর দন্ডায়মান হয়ে সমকোণ উৎপন্ন করেছে।
অতএব OC , AB এর উপর লম্ব।
এখন আমরা দেখাবো বৃত্তের কোনো জ্যা এর লম্ব বৃত্তের কেন্দ্রগামী হলে , জ্যা কে সমদ্বিখণ্ডিত করে ।
ধরা যাক O হল বৃত্তের কেন্দ্র এবং AB হল তার একটি জ্যা। OC , AB এর উপর লম্ব। আমাদের প্রমাণ করতে হবে  যে AC = BC .
যে AC = BC .
অঙ্কন : O , A এবং O , B যুক্ত করা হল।
প্রমাণ : এখন Δ AOC ও Δ BOC এর মধ্যে
OA = OB ( যেহেতু তারা O কেন্দ্রীয় বৃত্তের ব্যাসার্ধ )
OC সাধারণ বাহু।
[tex]\angle OCA = \angle OCB[/tex] ( যেহেতু [tex]OC \bot AB[/tex])
অতএব Δ AOC [tex] \cong [/tex] Δ BOC
সুতরাং আমরা বলতে পারি AC = BC .
অনুসিদ্ধান্ত : বৃত্তের কোনো জ্যা এর লম্বসমদ্বিখণ্ডক বৃত্তের কেন্দ্রগামী হবে।
(৩) দুটি বৃত্তের কেন্দ্র পরস্পরকে দুটি বিন্দুতে ছেদ করলে ওই ছেদ বিন্দুগামী সরলরেখা এবং বৃত্তের কেন্দ্রবিন্দুগামী সরলরেখা পরস্পরের লম্ব হবে।
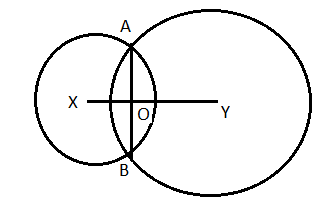
ধরা যাক X ও Y দুটি বৃত্তের কেন্দ্র , বৃত্ত দুটি পরস্পরকে A ও B বিন্দুতে ছেদ করেছে। আমাদের প্রমাণ করতে হবে XY সাধারণ জ্যা AB কে লম্বভাবে সমদ্বিখণ্ডিত করেছে।
অঙ্কন : X বিন্দু থেকে AB জ্যা এর লম্ব টানা হল যা AB কে O বিন্দুতে ছেদ করেছে। OY যুক্ত করা হল।
প্রমাণ : X কেন্দীয় বৃত্তের AB জ্যা এর উপর OX লম্ব। অতএব O হল AB এর মধ্যবিন্দু।
আবার Y কেন্দীয় বৃত্তের AB জ্যা এবং O হল AB এর মধ্যবিন্দু। অতএব [tex]OY \bot AB[/tex] হবে।
কোনো সরলরেখার উপর একটি বিন্দুতে কেবলমাত্র একটি লম্ব টানা যায়। সুতরাং OX ও OY একটি মাত্র সরলরেখায় অবস্থিত।
অতএব [tex]AB \bot XY[/tex]
আবার O , AB এর মধ্যবিন্দু
অতএব XY , AB কে লম্ব সমদ্বিখণ্ডিত করেছে।
(৪) কোনো বৃত্তের দুটি পরস্পর ছেদী জ্যা পরস্পরকে সমদ্বিখণ্ডিত করতে পারেনা , যদিনা উভয়ই বৃত্তের ব্যাসার্ধ হয়।
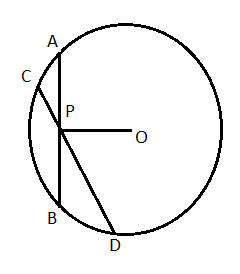 ধরা যাক O কেন্দীয় বৃত্তের AB ও CD দুটি জ্যা , তারা পরস্পরকে P বিন্দুতে এমনভাবে ছেদ করেছে যাতে P , AB এর মধ্যবিন্দু হয়।
ধরা যাক O কেন্দীয় বৃত্তের AB ও CD দুটি জ্যা , তারা পরস্পরকে P বিন্দুতে এমনভাবে ছেদ করেছে যাতে P , AB এর মধ্যবিন্দু হয়।
আমাদের প্রমাণ করতে হবে P , CD এর মধ্যবিন্দু নয়।
অঙ্কন : O , P যুক্ত করা হল।
প্রমাণ : P , AB এর মধ্যবিন্দু। অতএব [tex]OP \bot AB[/tex] .
AB ও CD উভয়েই P বিন্দুগামী। সুতরাং একই সঙ্গে AB ও CD উভয়েই OP এর সঙ্গে লম্ব হতে পারেনা। অতএব OP , CD এর উপর লম্ব হতে পারেনা।
আবার যেহেতু কোনো জ্যা এর মধ্যবিন্দুগামী সরলরেখা জ্যা এর উপর লম্ব হয় , তাই P , CD এর মধ্যবিন্দু হতে পারেনা।
(৫) বৃত্তের দুটি সমান দৈর্ঘ্যের জ্যা কেন্দ্র থেকে সমান দূরত্বে থাকে।
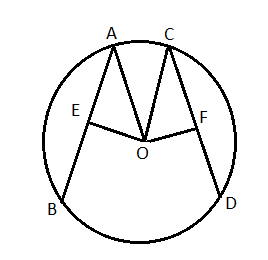 ধরা যাক O কেন্দ্রীয় বৃত্তের AB ও CD দুটি সমান দৈর্ঘ্যের জ্যা। আরো ধরা যাক [tex]OE \bot AB[/tex] এবং [tex]OF \bot CD[/tex] অর্থাৎ OE ও OF যথাক্রমে কেন্দ্ৰ O থেকে AB ও CD এর উপর দূরত্ব। প্রমাণ করতে হবে যে OE = OF .
ধরা যাক O কেন্দ্রীয় বৃত্তের AB ও CD দুটি সমান দৈর্ঘ্যের জ্যা। আরো ধরা যাক [tex]OE \bot AB[/tex] এবং [tex]OF \bot CD[/tex] অর্থাৎ OE ও OF যথাক্রমে কেন্দ্ৰ O থেকে AB ও CD এর উপর দূরত্ব। প্রমাণ করতে হবে যে OE = OF .
অঙ্কন : O , A এবং O , C যুক্ত করা হল।
প্রমাণ : দেখা যাচ্ছে [tex]OE \bot AB[/tex] এবং [tex]OF \bot CD[/tex]
অতএব E ও F যথাক্রমে AB ও CD এর মধ্যবিন্দু।
এখন AB = CD . অতএব [tex]\frac{1}{2} = AB = \frac{1}{2}CD \Rightarrow AE = CF[/tex]
এখন Δ AOE ও Δ COF এর মধ্যে
OA = OC ( যেহেতু বৃত্তের ব্যাসার্ধ )
AE = CF
এবং [tex]\angle AEO = \angle CFO[/tex]
অতএব Δ AOE [tex] \cong [/tex] Δ COF
সুতরাং আমরা বলতে পারি OE = OF
বৃত্ত ও কোণ সম্পর্কিত কয়েকটি সংজ্ঞা
(১) কেন্দ্রস্থ কোণ : কোনো বৃত্তের কেন্দ্রের সাথে ওই বৃত্তের যেকোনো বৃত্তচাপের প্রান্তবিন্দুদ্বয় যুক্ত করলে যে কোণ উৎপন্ন হয় , তাকে ওই বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ কোণ বলে।
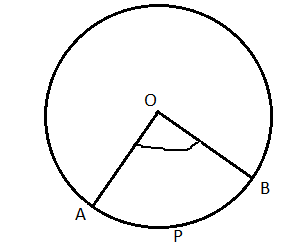
O হল একটি বৃত্তের কেন্দ্র। APB বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ কোণ হল [tex]\angle AOB[/tex].
(২) পরিধিস্থ কোণ : বৃত্তের কোনো একটি বৃত্তচাপের প্রান্তবিন্দুদ্বয়ের সাথে উহার বিপরীত বৃত্তচাপের উপর অবস্থিত কোনো একটি বিন্দু যোগ করলে যে কোণ উৎপন্ন হয় তাকে ওই বৃত্তচাপের অবস্থিত পরিধিস্থ কোণ বলে।
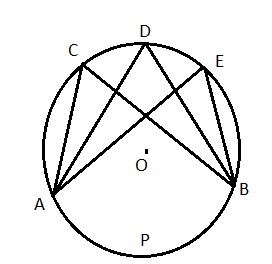
উপরের চিত্রে O কেন্দ্রীয় একটি বৃত্তে APB বৃত্তচাপের উপর অবস্থিত পরিধিস্থ কোণ হল [tex]\angle ACB,\angle ADB,\angle AEB[/tex] ইত্যাদি। সুতরাং কোনো বৃত্তচাপের উপর অবস্থিত কেন্দস্থ কোণ একটি এবং পরিধিস্থ কোণ অসংখ্য।
(৩) বৃত্তাংশস্থ কোণ : একটি বৃত্তাংশের জ্যা ওই বৃত্তাংশের বৃত্তচাপের উপর অবস্থিত কোনো বিন্দুতে যে কোণ উৎপন্ন করে তাকে বৃত্তাংশস্থ কোণ বলে।
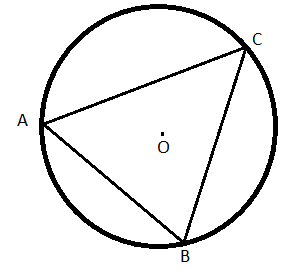
যেমন [tex]\angle ACB[/tex] , ACB বৃত্তাংশস্থ কোণ।
(৪) অর্ধবৃত্তস্থ কোণ : একটি বৃত্তের ব্যাস অর্ধবৃত্তচাপে যে কোণ উৎপন্ন করে তাকে অর্ধবৃত্তস্থ কোণ বলে।
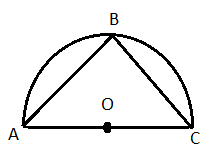
এখানে [tex]\angle ABC[/tex] হল অর্ধবৃত্তস্থ কোণ।
কোনো বৃত্তের একই বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুণ।
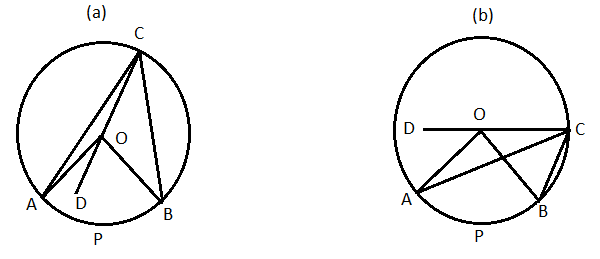
মনে করি APB এর উপর অবস্থিত কেন্দ্রস্থ কোণ হল [tex]\angle AOB[/tex] এবং পরিধিস্থ কোণ [tex]\angle ACB[/tex] . প্রমাণ করতে হবে [tex]\angle AOB = 2\angle ACB[/tex] .
অঙ্কন : C , O যুক্ত করে D বিন্দু পর্যন্ত বর্ধিত করা হল।
প্রমাণ : ΔAOC এর
OA = OC ( একই বৃত্তের ব্যাসার্ধ )
আবার ΔAOC এর CO বাহুকে D বিন্দু পর্যন্ত বর্ধিত করা হয়েছে।
অতএব বহিঃস্থকোণ [tex]\angle AOD = \angle OAC + \angle OCA = 2\angle OCA[/tex]
অনুরূপভাবে ΔBOC থেকে পাওয়া যাবে [tex]\angle BOD = 2\angle OCB[/tex]
এখন চিত্র (a)
[tex]∠AOB=∠AOD+∠BOD=2∠OCA+2∠OCB=2(∠OCA+∠OCB)=2∠ACB[/tex]
চিত্র (b)
[tex]∠AOB=∠BOD−∠AOD=2∠OCB−2∠OCA=2(∠OCB−∠OCA)=2∠ACB[/tex]
কয়েকটি প্রয়োগ
(১) ABC ত্রিভুজের পরিবৃত্তের কেন্দ্র O ; A এবং BC কেন্দ্রের বিপরীত পার্শে অবস্থিত। [tex]\angle BOC = {120^ \circ }[/tex] হলে [tex]\angle BAC[/tex] এর মান কত ?
সমাধান : 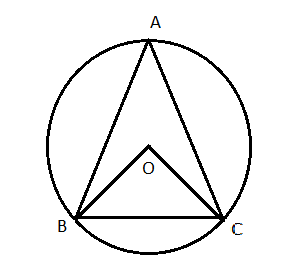
[tex]\angle BOC[/tex] এবং [tex]\angle BAC[/tex] কোণ দুটি O কেন্দ্রীয় বৃত্তের একই বৃত্তচাপের উপর অবস্থিত যথাক্রমে কেন্দ্রস্থ কোণ ও পরিধিস্থ কোণ।
অতএব [tex]\angle BAC = \frac{1}{2}\angle BOC = \frac{1}{2} \times {120^ \circ } = {60^ \circ }[/tex]
(২) ত্রিভুজ APB এবং ত্রিভুজ AOB হল যথাক্রমে O কেন্দ্রীয় বৃত্তের পরিবৃত্তিয় ও কেন্দ্রীয় ত্রিভুজ। [tex]\angle APB[/tex] এবং [tex]\angle AOB[/tex] মান নির্ণয় করো যখন [tex]\angle OAP = {25^ \circ }[/tex] এবং [tex]\angle OBP = {35^ \circ }[/tex] .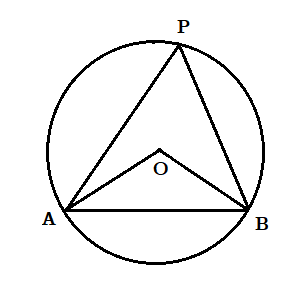
সমাধান : যেহেতু OA এবং OB হল O কেন্দ্রীয় বৃত্তের ব্যাসার্ধ
অতএব [tex]\angle OAB = \angle OBA = x[/tex] (মনে করি )
অতএব ত্রিভুজ AOB থেকে পাই [tex]\angle AOB = {180^ \circ } - 2x[/tex]
আবার পরিধিস্থ [tex]\angle APB = \frac{1}{2} \times \angle AOB = \frac{1}{2}\left( {{{180}^ \circ } - 2x} \right) = {90^ \circ } - x[/tex]
এখন ত্রিভুজ APB থেকে পাই
[tex]25∘+x+35∘+x+90∘−x=180∘⇒x+150∘=180∘⇒x=30∘[/tex]
অতএব [tex]\angle APB = {90^ \circ } - {30^ \circ } = {60^ \circ }[/tex]
এবং [tex]\angle AOB = 2 \times {60^ \circ } = {120^ \circ }[/tex]
(৩) দুটি সমান বৃত্ত পরস্পরকে A ও B বিন্দুতে ছেদ করে। A বিন্দুগামী একটি সরলরেখা একটি বৃত্তকে P বিন্দুতে এবং ওপর বৃত্তকে Q বিন্দুতে ছেদ করে প্রমাণ করো যে , BP = BQ .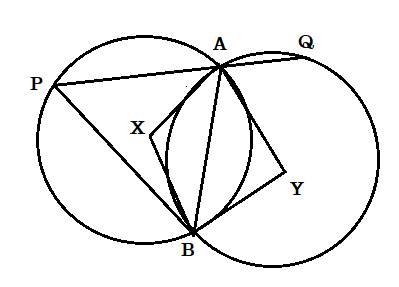
সমাধান :
অঙ্কন : মনে করি X ও Y যথাক্রমে প্রথম ও দ্বিতীয় বৃত্তের কেন্দ্র A , B ; A , X ; B , X ; A , Y ; B , Y যুক্ত করা হল।
প্রমাণ : ত্রিভুজ AXB এবং ত্রিভুজ AYB এর
AX = AY ( দুটি সমান বৃত্তের ব্যাসার্ধ ) ,
BX = BY ( দুটি সমান বৃত্তের ব্যাসার্ধ )
AB সাধারণ বহু
অতএব [tex]\Delta AXB \cong \Delta AYB[/tex]
অতএব [tex]\angle AXB = \angle AYB[/tex] ( অনুরূপ কোণ )
কিন্তু [tex]\angle APB = \frac{1}{2}\angle AXB[/tex] ( একই চাপের উপর অবস্থিত [tex]\angle APB[/tex] পরিধিস্থ কোণ এবং [tex]\angle AXB[/tex] কেন্দ্রস্থ কোণ )
অনুরূপে [tex]\angle AQB = \frac{1}{2}\angle AYB[/tex]
অতএব [tex]\angle APB = \angle AQB[/tex] যেহেতু [tex]\angle AXB = \angle AYB[/tex]
অর্থাৎ [tex]\angle QPB = \angle PQB[/tex]
ত্রিভুজ PBQ এর
[tex]\angle QPB = \angle PQB[/tex]
অতএব BP = BQ
(৪) ABC একটি সমদ্বিবাহু ত্রিভুজ যার AB = AC , BC এর যে পাশে ত্রিভুজ ABC অবস্থিত , সেই পাশেই ত্রিভুজ DBC অবস্থিত এবং [tex]\angle BAC = 2\angle BDC[/tex] . প্রমাণ করো যে , A কে কেন্দ্র করে AB ব্যাসার্ধ নিয়ে যে বৃত্ত অঙ্কন করা যাবে , D বিন্দু সেই বৃত্তের উপর অবস্থিত হবে। 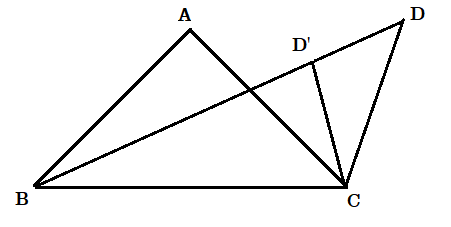
সমাধান : মনে করি D বিন্দু সেই বৃত্তের উপর অবস্থিত নয়। তাহলে মনে করি বৃত্তটি D ' বিন্দুতে BD কে ছেদ করেছে।
অতএব [tex]\angle BAC = 2\angle BD'C[/tex] ( যেহেতু [tex]\angle BAC[/tex] এবং [tex]\angle BD'C[/tex] একই বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ ও পরিধিস্থ কোণ )
কিন্তু [tex]\angle BAC = 2\angle BDC[/tex] ( কল্পনানুসারে )
অতএব [tex]\angle BD'C = \angle BDC[/tex]
কিন্তু এটা অসম্ভব যদি না D ও D ' বিন্দু সমাপতিত হয় , কারণ ত্রিভুজ DD'C এর বহিঃস্থ [tex]\angle BD'C > [/tex] অন্তঃস্থ বিপরীত [tex]\angle BDC[/tex] .
একই বৃত্তাংশস্থ সকল কোণের মান সমান
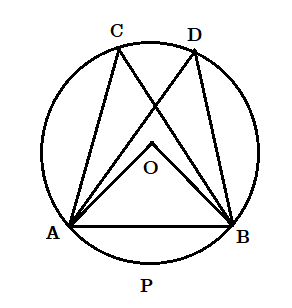
মনে করি [tex]\angle ACB[/tex] এবং [tex]\angle ADB[/tex] কোণ দুটি O কেন্দ্রীয় বৃত্তের ACDB বৃত্তাংশের উপর অবস্থিত। আমাদের প্রমাণ করতে হবে যে ACDB বৃত্তাংশস্থ সকল কোণের মান সমান। যেহেতু [tex]\angle ACB[/tex] এবং [tex]\angle ADB[/tex] কোণ দুটি ওই বৃত্তাংশস্থ যেকোনো দুটি কোণ , সুতরাং [tex]\angle ACB[/tex] এবং [tex]\angle ADB[/tex] কোণ দুটি পরস্পর সমান প্রমাণিত হলে এই উপপাদ্যটি প্রমাণিত হবে।
অঙ্কন : O , A এবং O , B যুক্ত করা হল।
প্রমাণ : চাপ APB এর অবস্থিত কেন্দ্রস্থ কোণ [tex]\angle AOB[/tex] এবং পরিধিস্থ কোণ [tex]\angle ACB[/tex] ও [tex]\angle ADB[/tex]
অতএব [tex]\angle AOB = 2\angle ACB[/tex]
এবং [tex]\angle AOB = 2\angle ADB[/tex]
সুতরাং
[tex]2∠ACB=2∠ADB⇒∠ACB=∠ADB[/tex]
অনুসিদ্ধান্ত
(1) বৃত্তের সমান সমান চাপের উপর অবস্থিত পরিধিস্থ সকল কোণ সমান। বিপরীতক্রমে বৃত্তের একাধিক পরিধিস্থ কোণ সমান হলে , সেই কোণগুলি যে বৃত্তচাপের উপর অবস্থিত সেই চাপগুলিও পরস্পর সমান হবে।
(2) যদি দুটি বৃত্তের সংযোগ রেখাংশ তার একই পাশে অপর দুটি বিন্দুতে দুটি সমান কোণ উৎপন্ন করে , তাহলে চারটি বিন্দু সমবৃত্তস্থ হবে।
প্রমাণ : 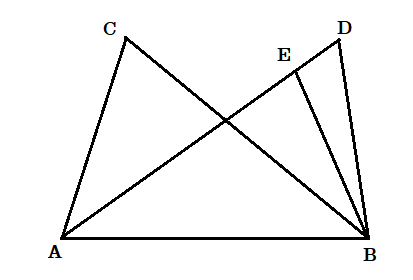 মনে করি A ও B দুটি সংযোগ সরলরেখার একই পাশে C ও D দুটি বিন্দু। C ও D দুটি বিন্দুতে [tex]\angle ACB[/tex] এবং [tex]\angle ADB[/tex] দুটি সমান কোণ উৎপন্ন হয়েছে। যেহেতু A , B ও C তিনটি অসমরেখ বিন্দু সুতরাং ওই তিনটি বিন্দু দিয়ে একটি বৃত্ত অঙ্কন করা যাবে , যা D বিন্দুগামী হবে নতুবা AD কে বা বর্ধিত AD কে কোনো বিন্দুতে ছেদ করবে।
মনে করি A ও B দুটি সংযোগ সরলরেখার একই পাশে C ও D দুটি বিন্দু। C ও D দুটি বিন্দুতে [tex]\angle ACB[/tex] এবং [tex]\angle ADB[/tex] দুটি সমান কোণ উৎপন্ন হয়েছে। যেহেতু A , B ও C তিনটি অসমরেখ বিন্দু সুতরাং ওই তিনটি বিন্দু দিয়ে একটি বৃত্ত অঙ্কন করা যাবে , যা D বিন্দুগামী হবে নতুবা AD কে বা বর্ধিত AD কে কোনো বিন্দুতে ছেদ করবে।
মনে করি এক্ষেত্রে বৃত্তটি AD কে E বিন্দুতে ছেদ করেছে। B , E যুক্ত করা হল।
[tex]\angle ACB = \angle AEB[/tex] হবে যেহেতু উহারা একই বৃত্তাংশস্থ কোণ।
কিন্তু [tex]\angle ACB = \angle ADB[/tex]
অতএব [tex]\angle AEB = \angle ADB[/tex] হবে। কিন্তু ইহা অসম্ভব যদিনা E , D বিন্দু সমাপতিত হয়। কারণ ত্রিভুজ BED এর বহিঃস্থ কোণ [tex]\angle AEB > \angle ADB[/tex] .
অতএব A , B , C , D সমবৃত্তস্থ।
কয়েকটি প্রয়োগ
(১) প্রমাণ করো কোনো বৃত্তে একই বৃত্তাংশে অবস্থিত সমস্ত কোণের সমদ্বিখণ্ডকগুলি একটি নির্দিষ্ট বিন্দুগামী।
প্রমাণ : 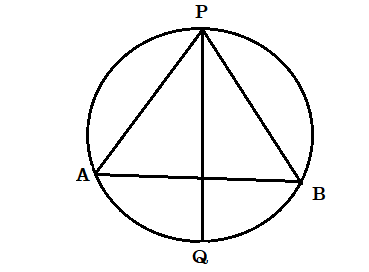 মনে করি O কেন্দ্রীয় একটি বৃত্তের APB বৃত্তাংশে অবস্থিত একটি কোণ [tex]\angle APB[/tex] . [tex]\angle APB[/tex] কোণের সমদ্বিখণ্ডক PAQB বৃত্তকে Q বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে ইহা একটি নির্দিষ্ট বিন্দুগামী।
মনে করি O কেন্দ্রীয় একটি বৃত্তের APB বৃত্তাংশে অবস্থিত একটি কোণ [tex]\angle APB[/tex] . [tex]\angle APB[/tex] কোণের সমদ্বিখণ্ডক PAQB বৃত্তকে Q বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে ইহা একটি নির্দিষ্ট বিন্দুগামী।
আমরা জানি [tex]\angle APQ = \angle BPQ[/tex]
অতএব বৃত্তচাপ AQ = বৃত্তচাপ BQ .
সুতরাং Q হল বৃত্তচাপ AQB এর মধ্যবিন্দু।
অতএব AB নির্দিষ্ট হলে , Q একটি নির্দিষ্ট বিন্দু।
অতএব বৃত্তচাপের উপরে P বিন্দুর যেকোনো অবস্থানের জন্য [tex]\angle APB[/tex] এর সমদ্বিখণ্ডক উহার বিপরীত চাপের মধ্যবিন্দুগামী হবে।
(২)
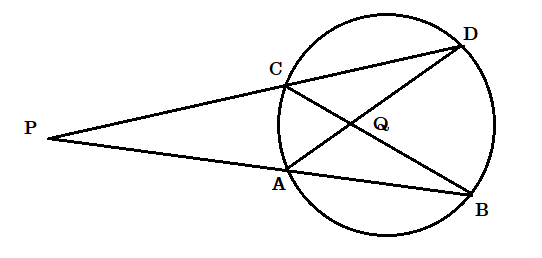
উপরের চিত্র থেকে প্রমাণ করো [tex]\angle PCB = \angle PAD[/tex]
চিত্রে AD ও BC পরস্পর Q বিন্দুতে ছেদ করেছে।
অতএব [tex]\angle CQD = \angle AQB[/tex] .............(i)
আবার [tex]\angle ADC = \angle ABC[/tex] ( একই চাপের উপর অবস্থিত ) .............(ii)
অতএব ত্রিভুজ CDQ এর বহিঃকোণ
[tex]∠PCB=∠CDQ+∠CQD=∠CDA+∠CQD=∠ABC+∠AQB[(i),(ii)]=∠ABQ+∠AQB=∠QAP[/tex]
ত্রিভুজ ABQ এর বহিঃকোণ
[tex] = \angle PAD[/tex]
(৩) ABC সমবাহু ত্রিভুজটি একটি বৃত্তে অন্তর্লিখিত। BC উপচাপের উপর P যেকোনো একটি বিন্দু প্রমাণ করো যে PA = PB + PC
অঙ্কন : 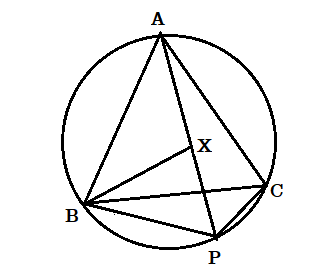 PA থেকে PB এর সমান করে PX অংশ কেটে নেওয়া হল। BX যুক্ত করা হল।
PA থেকে PB এর সমান করে PX অংশ কেটে নেওয়া হল। BX যুক্ত করা হল।
প্রমাণ : যেহেতু ত্রিভুজ PBX এর PB = PX
অতএব [tex]\angle PXB = \angle PBX[/tex]
আবার [tex]\angle BPX = \angle ACB[/tex] ( একই বৃত্তাংশস্থ কোণ )
= [tex]{60^ \circ }[/tex] ( যেহেতু ABC সমবাহু ত্রিভুজ )
অতএব
[tex]∠PXB+∠PBX=120∘⇒∠PXB=∠PBX=60∘[/tex]
অতএব PBX সমবাহু ত্রিভুজ
অতএব [tex]\angle PXB = \angle CBA[/tex] প্রত্যেকেই [tex]{60^ \circ }[/tex]
[tex]⇒∠PBC=∠PBX−∠CBX⇒∠CBA−∠CBX=∠XBA[/tex]
এবার ত্রিভুজ AXB ও ত্রিভুজ CPB এর
AB = BC ( যেহেতু ABC সমবাহু ত্রিভুজ )
BX = BP ( যেহেতু PBX সমবাহু ত্রিভুজ )
অন্তৰ্ভূত [tex]\angle XBA[/tex] = অন্তৰ্ভূত [tex]\angle PBC[/tex] ( প্রমাণিত )
অতএব ত্রিভুজ AXB [tex] \cong [/tex] ত্রিভুজ CPB
অতএব AX = PC ( অনুরূপ বাহু )
অতএব PA = PX + XA = PB + PC
অর্ধবৃত্তস্থ কোণ সমকোণ
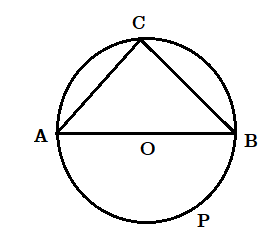 মনে করি O কেন্দ্রীয় বৃত্তের [tex]\angle ACB[/tex] হল অর্ধবৃত্তস্থ কোণ। আমাদের প্রমাণ করতে হবে যে [tex]\angle ACB[/tex] = 1 সমকোণ
মনে করি O কেন্দ্রীয় বৃত্তের [tex]\angle ACB[/tex] হল অর্ধবৃত্তস্থ কোণ। আমাদের প্রমাণ করতে হবে যে [tex]\angle ACB[/tex] = 1 সমকোণ
প্রমাণ : একই বৃত্তচাপ APB এর উপর অবস্থিত [tex]\angle AOB[/tex] কেন্দ্রস্থ কোণ এবং [tex]\angle ACB[/tex] পরিধিস্থ কোণ।
অতএব [tex]\angle AOB = 2\angle ACB[/tex]
কিন্তু AOB একটি রেখাংশ।
অতএব [tex]\angle AOB[/tex] = 2 সমকোণ।
অর্থাৎ [tex]2\angle ACB[/tex] = 2 সমকোণ।
অতএব [tex]\angle ACB[/tex] = 1 সমকোণ।
বিকল্প পদ্ধতি
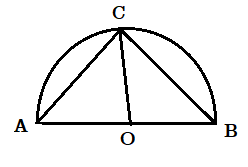 মনে করি ACB একটি অর্ধবৃত্ত , যার কেন্দ্র O এবং [tex]\angle ACB[/tex] হল অর্ধবৃত্তস্থ কোণ।
মনে করি ACB একটি অর্ধবৃত্ত , যার কেন্দ্র O এবং [tex]\angle ACB[/tex] হল অর্ধবৃত্তস্থ কোণ।
প্রমাণ করতে হবে যে [tex]\angle ACB[/tex] = 1 সমকোণ .
অঙ্কন : C , O যুক্ত করা হল।
প্রমাণ : ত্রিভুজ AOC এর OA = OC ( একই বৃত্তের ব্যাসার্ধ )
অতএব [tex]\angle OCA = \angle OAC[/tex] .
আবার ত্রিভুজ BOC এর OB = OC
অতএব [tex]\angle OCB = \angle OBC[/tex]
অতএব
[tex]∠OCA+∠OCB=∠OAC+∠OBC⇒∠ACB=∠BAC+∠ABC⇒2∠ACB=∠ACB+∠BAC+∠ABC=180∘⇒∠ACB=90∘[/tex]
অর্থাৎ [tex]\angle ACB[/tex] = 1 সমকোণ
অনুসিদ্ধান্ত
(১) অর্ধবৃত্ত অপেক্ষা বৃহত্তর বৃত্তাংশস্থ কোণ সূক্ষকোণ।
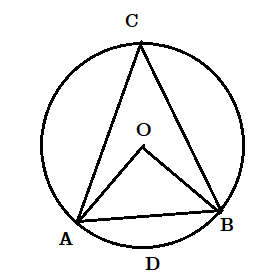 ACB বৃত্তাংশ অর্ধবৃত্ত অপেক্ষা বৃহত্তর।
ACB বৃত্তাংশ অর্ধবৃত্ত অপেক্ষা বৃহত্তর।
অতএব ADB একটি উপচাপ।
অতএব ওই চাপের উপর অবস্থিত কেন্দ্রস্থ কোণ [tex]\angle AOB[/tex] , 2 সমকোণ অপেক্ষা ক্ষুদ্রত্তর।
যেহেতু [tex]\angle ACB[/tex] ওই চাপের উপর অবস্থিত পরিধিস্থ কোণ ,
অতএব [tex]\angle ACB[/tex] এক সমকোণ অপেক্ষা ক্ষুদ্রত্তর অর্থাৎ [tex]\angle ACB[/tex] সূক্ষকোণ।
(২) অর্ধবৃত্ত অপেক্ষা ক্ষুদ্রত্তর বৃত্তাংশস্থ কোণ স্থলকোণ।
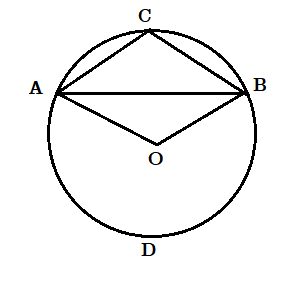 ACB বৃত্তাংশ অর্ধবৃত্ত অপেক্ষা ক্ষুদ্রত্তর।
ACB বৃত্তাংশ অর্ধবৃত্ত অপেক্ষা ক্ষুদ্রত্তর।
অতএব ADB একটি অধিচাপ।
অতএব ওই চাপের উপর অবস্থিত কেন্দ্রস্থ কোণ প্রবৃদ্ধ [tex]\angle AOB[/tex] , 2 সমকোণ অপেক্ষা বৃহত্তর।
যেহেতু [tex]\angle ACB[/tex] ওই চাপের উপর অবস্থিত পরিধিস্থ কোণ ,
অতএব [tex]\angle ACB[/tex] এক সমকোণ অপেক্ষা বৃহত্তর।
কয়েকটি প্রয়োগ
(১) একটি সমকোণী ত্রিভুজের অতিভুজকে ব্যাস করে অঙ্কিত বৃত্ত অবশই সমকৌণিক বিন্দু দিয়ে যাবে।
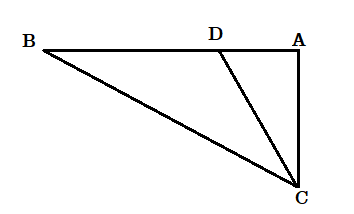 মনে করি ΔABC একটি সমকোণী ত্রিভুজ , যার [tex]\angle A[/tex] হল সমকোণ। আমাদের প্রমাণ করতে হবে যে BC কে ব্যাস করে অঙ্কিত বৃত্ত A বিন্দু দিয়ে যাবে।
মনে করি ΔABC একটি সমকোণী ত্রিভুজ , যার [tex]\angle A[/tex] হল সমকোণ। আমাদের প্রমাণ করতে হবে যে BC কে ব্যাস করে অঙ্কিত বৃত্ত A বিন্দু দিয়ে যাবে।
প্রমাণ : মনে করি বৃত্তটি A বিন্দু দিয়ে যায় না , তাহলে ধরা যাক বৃত্তটি AB কে D বিন্দুতে ছেদ করেছে। সেই অনুসারে [tex]\angle BDC[/tex] = 1 সমকোণ ( কারণ অর্ধবৃত্তস্থ কোণ সমকোণ )
কিন্তু [tex]\angle BAC[/tex] = 1 সমকোণ
অতএব [tex]\angle BAC = \angle BDC[/tex]
কিন্তু তা অসম্ভব যদি না D ও A সমাপতিত হয়।
কারণ ত্রিভুজ ADC এর বহিঃস্থ [tex]\angle BDC[/tex] > অন্তঃস্থ বিপরীত [tex]\angle BAC[/tex] .
অতএব বৃত্তটি A বিন্দু দিয়ে যাবে।
[ D বিন্দুটি বর্ধিত AD বাহুর উপর থাকলে অনুরূপ প্রমাণ সম্ভব ]
(২) প্রমাণ করো যে একটি ত্রিভুজের বৃহত্তম বাহু অপেক্ষা ক্ষুদ্রত্তর দুটি বাহুকে ব্যাস করে অঙ্কিত বৃত্ত দুটির ছেদ বিন্দু তৃতীয় বাহুর উপর অবস্থিত হবে।
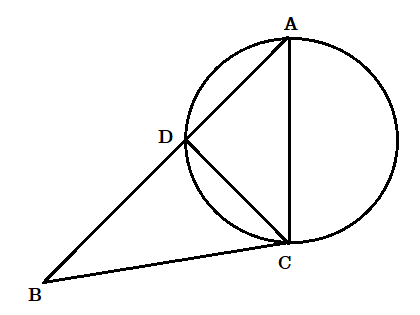 মনে করি ABC একটি ত্রিভুজ AC ও BC বাহু দুটি ক্ষুদ্রত্তর বাহু। AC কে ব্যাস করে অঙ্কিত বৃত্ত মনে করি AB কে D বিন্দুতে ছেদ করে।
মনে করি ABC একটি ত্রিভুজ AC ও BC বাহু দুটি ক্ষুদ্রত্তর বাহু। AC কে ব্যাস করে অঙ্কিত বৃত্ত মনে করি AB কে D বিন্দুতে ছেদ করে।
আমাদের প্রমাণ করতে হবে যে BC কে ব্যাস করে অঙ্কিত বৃত্ত ও D বিন্দুগামী হবে।
অঙ্কন : D , C যুক্ত করা হল।
প্রমাণ : যেহেতু [tex]\angle ADC[/tex] অর্ধবৃত্তস্থ কোণ ,
অতএব [tex]\angle ADC[/tex] = 1 সমকোণ
অতএব [tex]\angle BDC[/tex] = 1 সমকোণ
অতএব ত্রিভুজ CDB সমকোণী ত্রিভুজ।
অতএব BC কে ব্যাস করে অঙ্কিত বৃত্ত অবশ্যই D বিন্দুগামী হবে।
বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক
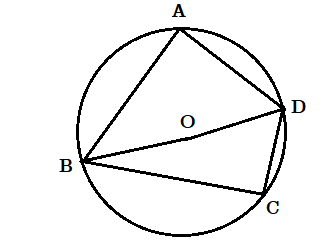 মনে করি ABCD একটি বৃত্তস্থ চতুর্ভুজ এবং O হল কেন্দ্র।
মনে করি ABCD একটি বৃত্তস্থ চতুর্ভুজ এবং O হল কেন্দ্র।
প্রমাণ করতে হবে যে ,
(i) [tex]\angle BAD + \angle BCD[/tex] = 2 সমকোণ
(ii) [tex]\angle ABC + \angle ADC[/tex] = 2 সমকোণ
অঙ্কন : B , O এবং D , O যুক্ত করা হল।
প্রমাণ : BCD বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ কোণ প্রবৃদ্ধ [tex]\angle BOD[/tex] এবং পরিধিস্থ কোণ [tex]\angle BAD[/tex]
অতএব [tex]\angle BOD = 2\angle BAD[/tex]
অর্থাৎ [tex]\angle BAD = \frac{1}{2}\angle BOD[/tex]
আবার BAD বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ কোণ [tex]\angle BOD[/tex] এবং পরিধিস্থ কোণ [tex]angle BCD[/tex] .
অতএব [tex]\angle BCD = \frac{1}{2}\angle BOD[/tex]
অতএব [tex]\angle BAD + \angle BCD = [/tex] [tex]\frac{1}{2}\angle BOD[/tex]+[tex]\frac{1}{2}[/tex]প্রবৃদ্ধ [tex]\angle BOD[/tex]
[tex] \Rightarrow \angle BAD + \angle BCD = \frac{1}{2} \times {360^ \circ } = {180^ \circ }[/tex]
অর্থাৎ [tex]\angle BAD + \angle BCD[/tex] = 2 সমকোণ
অনুরূপে A , O এবং O , C যুক্ত করে প্রমাণ করা যায় [tex]\angle ABC + \angle ADC[/tex] = 2 সমকোণ
বিকল্প পদ্ধতি :
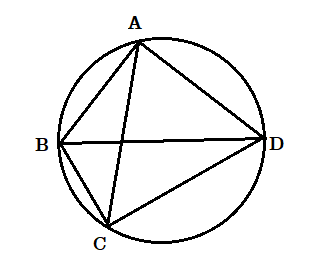 মনে করি ABCD বৃত্তস্থ চতুর্ভুজ।
মনে করি ABCD বৃত্তস্থ চতুর্ভুজ।
প্রমাণ করতে হবে যে
(i) [tex]\angle BAD + \angle BCD[/tex] = 2 সমকোণ
(ii) [tex]\angle ABC + \angle ADC[/tex] = 2 সমকোণ
অঙ্কন : AC ও BD কর্ণ দুটি টানা হল।
প্রমাণ : [tex]\angle BAC = \angle BDC[/tex] ( একই বৃত্তাংশস্থ কোণ )
[tex]\angle CAD = \angle CBD[/tex] ( একই বৃত্তাংশস্থ কোণ )
অতএব
[tex]∠BAD=∠BAC+∠CAD=∠BDC+∠CBD⇒∠BAD+∠BCD=∠BDC+∠CBD+∠BCD=180∘[/tex]
অর্থাৎ [tex]\angle BAD + \angle BCD[/tex] = 2 সমকোণ
অনুরূপভাবে দেখানো যায় [tex]\angle ABC + \angle ADC = \angle DAC + \angle DCA + \angle ADC = {180^ \circ }[/tex]
অর্থাৎ [tex]\angle ABC + \angle ADC[/tex] = 2 সমকোণ
কয়েকটি প্রয়োগ
(১) প্রমাণ করো যে বৃত্তস্থ সামান্তরিক অবশ্যই আয়তক্ষেত্র হবে।
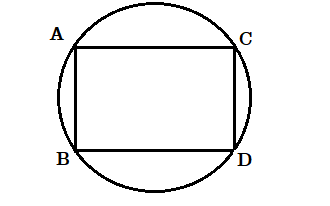 মনে করি ABCD সামান্তরিকটি বৃত্তস্থ সামান্তরিক।
মনে করি ABCD সামান্তরিকটি বৃত্তস্থ সামান্তরিক।
আমাদের প্রমাণ করতে হবে যে ABCD সামান্তরিকটি হল আয়তক্ষেত্র।
প্রমাণ : ABCD একটি সামান্তরিক।
অতএব [tex]\angle ABC = \angle ADC[/tex].
আবার ABCD সামান্তরিকটি বৃত্তস্থ
অতএব
[tex]∠ABC+∠ADC=180∘⇒2∠ABC=180∘⇒∠ABC=90∘[/tex]
অতএব ABCD চতুর্ভুজটি আয়তক্ষেত্র।
(২) ABCD একটি বৃত্তস্থ চতুর্ভুজ। [tex]\angle DAB[/tex] ও [tex]\angle BCD[/tex] সমদ্বিখণ্ডকদ্বয় বৃত্তকে X এবং Y বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে XY ওই বৃত্তের ব্যাস।
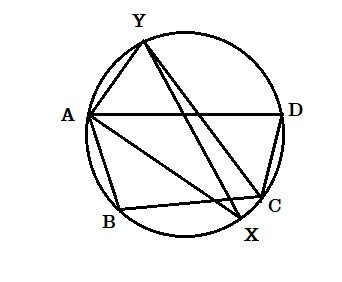 অঙ্কন : A , Y যুক্ত করা হল।
অঙ্কন : A , Y যুক্ত করা হল।
প্রমাণ : [tex]\angle YAD[/tex] ও [tex]\angle YCD[/tex] একই চাপের উপরে অবস্থিত
অতএব [tex]\angle YAD = \angle YCD = \frac{1}{2}\angle BCD[/tex] ( যেহেতু CY , [tex]\angle BCD[/tex] এর সমদ্বিখণ্ডক )
অতএব
[tex]∠XAY=∠XAD+∠YAD=12∠BAD+12∠BCD[/tex]
( যেহেতু AX , [tex]\angle DAB[/tex] )
[tex]=12(∠BAD+∠BCD)=12×180∘[/tex]
( যেহেতু ABCD বৃত্তস্থ চতুর্ভুজ )
[tex] = {90^ \circ }[/tex]
অতএব XBAY অর্ধবৃত্ত। অতএব XY বৃত্তের ব্যাস ।
*****