ত্রিকোণমিতিক অনুপাত

 ত্রিকোণমিতিক অনুপাত  ( Trigonometrical Ratios )

 ত্রিকোণমিতিক অনুপাত নির্ণয় 

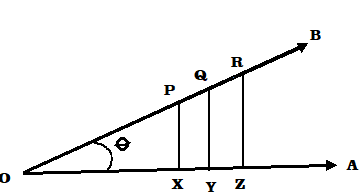
মনে করি AO রেখাটি ঘড়ির কাঁটার বিপরীতদিকে ঘুরে OB অবস্থানে এসে OA রেখার সঙ্গে [tex]\angle AOB[/tex] কোণ উৎপন্ন করেছে। এবার কোণের OB বাহুর উপরে P , Q , R .... যেকোনো সংখ্যক বিন্দু নিয়ে OA বাহুর উপরে যথাক্রমে PX , QY , RZ , ..... লম্ব টানা হল। ফলে XOP , YOQ , ZOR ... যে সমকোণী ত্রিভুজ পাওয়া গেল তারা পরস্পর সদৃশ। এবার সদৃশ ত্রিভুজের ধর্ম থেকে আমরা পাই 

(i) [tex]\frac{{PX}}{{OP}} = \frac{{QY}}{{OQ}} = \frac{{RZ}}{{OR}} = .....[/tex]

(ii) [tex]\frac{{OX}}{{OP}} = \frac{{OY}}{{OQ}} = \frac{{OZ}}{{OR}} = .....[/tex]

(iii) [tex]\frac{{PX}}{{OX}} = \frac{{QY}}{{OY}} = \frac{{RZ}}{{OZ}} = .....[/tex]

(iv) [tex]\frac{{OP}}{{PX}} = \frac{{OQ}}{{QY}} = \frac{{OR}}{{RZ}} = .....[/tex]

(v) [tex]\frac{{OP}}{{OX}} = \frac{{OQ}}{{OY}} = \frac{{OR}}{{OZ}} = ......[/tex]

(vi) [tex]\frac{{OX}}{{PX}} = \frac{{OY}}{{QY}} = \frac{{OZ}}{{RZ}} = .....[/tex]

তাহলে দেখা যাচ্ছে এক প্রস্থ সদৃশ সমকোণী ত্রিভুজের কোনো একটি সূক্ষকোণের সাপেক্ষে 

(i) লম্ব : অতিভুজ বা লম্ব এবং অতিভুজের অনুপাত গুলি সমান , অনুরূপে (ii) ভূমি : অতিভুজ বা ভূমি এবং অতিভুজের অনুপাত , (iii) লম্ব : অতিভুজ বা লম্ব এবং অতিভুজের অনুপাত গুলি পরস্পর সমান। সুতরাং বলা যায় অনুপাত গুলির মান ত্রিভুজগুলির বাহুর দৈর্ঘ্যের উপর নির্ভরশীল নয়। অনুপাতগুলির মান সম্পূর্ণরূপে সূক্ষকোণটির পরিমানের উপর নির্ভরশীল। 

যেহেতু ত্রিভুজগুলি প্রত্যেকটি সমকোণী ত্রিভুজ এবং তাদের একটি সাধারণ সূক্ষকোণ [tex]\theta [/tex] তাই এই ঘটনা ঘটেছে। সাধারণ সূক্ষকোণ [tex]\theta [/tex] এর মান যাই হোকনা কেন প্রতিক্ষেত্রে অনুরূপ ফল পাওয়া যাবে। 

তাহলে দেখা যাচ্ছে সদৃশ সমকোণী ত্রিভুজের যেকোনো একটি সাধারণ সূক্ষকোণের পরিপ্রেক্ষিতে বাহুগুলির পারস্পরিক অনুপাতের একটি নির্দিষ্ট মান পাওয়া যায়। এই সত্যের উপরে ভিত্তি করে ত্রিকোণমিতিক অনুপাত প্রতিষ্ঠিত। আবার আমরা দেখেছে ত্রিভুজের তিনটি বাহুর দুটি দুটি করে নিয়ে মোট ছয় প্রকারের অনুপাত পাওয়া যায়। তাই এই ছয় প্রকারের অনুপাতকে আলাদা আলাদা ভাবে চিহ্নিত করার জন্য ত্রিকোনমিতিতে তাদের আলাদা আলাদা নাম দেওয়া হয়েছে এই অনুপাতগুলিকে ত্রিকোণমিতিক অনুপাত বলা হয়। 

 

ত্রিকোণমিতিক অনুপাত ও তাদের নাম ( Different types of Trigonometrical Ratios )

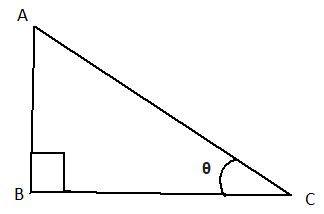এখানে  ABC ত্রিভুজের [tex]\angle ABC[/tex] = এক সমকোণ। অতএব AC = অতিভুজ এবং সূক্ষকোণ [tex]\angle ACB[/tex] এর পরিপেক্ষিতে BC হল ভূমি এবং AB হল লম্ব।

মনে করি [tex]\angle ACB = \theta [/tex] . এখন 

1. [tex]\frac{{AB}}{{AC}} = sine\theta [/tex] যাকে সংক্ষেপে লেখা হয় [tex]\sin \theta [/tex]
2. [tex]\frac{{BC}}{{AC}} = {\mathop{\rm cosine}\nolimits} \theta [/tex] যাকে সংক্ষেপে লেখা হয় [tex]\cos \theta [/tex]
3. [tex]\frac{{AB}}{{BC}} = \tan gent\theta [/tex] যাকে সংক্ষেপে লেখা হয় [tex]\tan \theta [/tex]
4. [tex]\frac{{AC}}{{AB}} = \cos ecant\theta [/tex] যাকে সংক্ষেপে লেখা হয় [tex]\cos ec\theta [/tex]
5. [tex]\frac{{AC}}{{BC}} = \sec ant\theta [/tex] যাকে সংক্ষেপে লেখা হয় [tex]\sec \theta [/tex]
6. [tex]\frac{{BC}}{{AB}} = cotangent\theta [/tex] যাকে সংক্ষেপে লেখা হয় [tex]\cot\theta [/tex]

বিশেষ ভাবে মনে রাখতে হবে যে আলোচ্য সূক্ষকোণের বিপরীত বাহুটিকে লম্ব ধরতে হবে এবং অতিভুজ ছাড়া অন্য বাহুটিকে ভূমি ধরতে হবে। আরো মনে রাখতে হবে যে , যেকোনো অনুপাতের মতো এই অনুপাত গুলি শুদ্ধ সংখ্যা , যার কোনো একক নেই। 

 

ত্রিকোণমিতিক অনুপাতের ধর্ম ( Properties of Trigonometrical Ratios)

  মনে করি [tex]\sin \theta [/tex] এর বর্গ নিতে হবে , অর্থাৎ [tex]{\left( {\sin \theta } \right)^2}[/tex] নিতে হবে। আমাদের লেখার সুবিধার জন্য আমরা সাধারণত [tex]{\left( {\sin \theta } \right)^2} = {\sin ^2}\theta [/tex] লিখি। কিন্তু খেয়াল রাখতে হবে [tex]{\left( {\sin \theta } \right)^2} \ne \sin {\theta ^2}[/tex] .

অনুরূপ ভাবে [tex]{\left( {\cos \theta } \right)^2} = {\cos ^2}\theta ,{\left( {\tan \theta } \right)^2} = {\tan ^2}\theta [/tex] ইত্যাদি। 

ত্রিকোণমিতিক অনুপাত গুলির পারস্পরিক সম্পর্ক ( Relations between Different Trigonometrical Ratios )

(A) Reciprocal relation 

(1) উপরের চিত্র থেকে দেখা যাচ্ছে [tex]\sin \theta  = \frac{{AB}}{{AC}}[/tex] . আবার [tex]\cos ec\theta  = \frac{{AC}}{{AB}}[/tex] . একটু লক্ষ্য করলে দেখা যাচ্ছে ত্রিকোণমিতিক অনুপাত দুটি একটি অন্যটির ব্যস্ত অনুপাতের সমান , অর্থাৎ 

[tex] $$\begin{array}{l} \sin \theta  = \frac{{AB}}{{AC}} = \frac{1}{{\frac{{AC}}{{AB}}}} = \frac{1}{{\cos ec\theta }}\\  \Rightarrow \sin \theta  = \frac{1}{{\cos ec\theta }}\\  \Rightarrow \cos ec\theta  = \frac{1}{{\sin \theta }} \end{array}$$ [/tex]

(2) আবার 

[tex] $$\begin{array}{l} \cos \theta  = \frac{{BC}}{{AC}} = \frac{1}{{\frac{{AC}}{{BC}}}} = \frac{1}{{\sec \theta }}\\  \Rightarrow \cos \theta  = \frac{1}{{\sec \theta }}\\  \Rightarrow \sec \theta  = \frac{1}{{\cos \theta }} \end{array}$$ [/tex]

এখানেও একটি অন্যটির ব্যাস্তানুপাত। 

(3) আবার 

[tex] $$\begin{array}{l} \tan \theta  = \frac{{AB}}{{BC}} = \frac{1}{{\frac{{BC}}{{AB}}}} = \frac{1}{{\cot \theta }}\\  \Rightarrow \tan \theta  = \frac{1}{{\cot \theta }}\\  \Rightarrow \cot \theta  = \tan \theta  \end{array}$$ [/tex]

এখানেও একটি অন্যটির ব্যাস্তানুপাত। 

(B) Quotient relations 

আবার দেখো 

[tex]\frac{{\sin \theta }}{{\cos \theta }} = \frac{{\frac{{AB}}{{AC}}}}{{\frac{{BC}}{{AC}}}} = \frac{{AB}}{{BC}} = \tan \theta [/tex]

অতএব [tex]\cot \theta  = \frac{1}{{\tan \theta }} = \frac{1}{{\frac{{\sin \theta }}{{\cos \theta }}}} = \frac{{\cos \theta }}{{\sin \theta }}[/tex]

 

(C) Square relation 

(1) আবার চিত্রে সমকোণী ত্রিভুজ ABC থেকে পাই ,

[tex]A{B^2} + B{C^2} = A{C^2}[/tex]

এই সম্পর্কের উভয়পাশে [tex]A{C^2}[/tex] দিয়ে ভাগ করে পাই 

[tex] $$\begin{array}{l} \frac{{A{B^2} + B{C^2}}}{{A{C^2}}} = \frac{{A{C^2}}}{{A{C^2}}}\\  \Rightarrow {\left( {\frac{{AB}}{{AC}}} \right)^2} + {\left( {\frac{{BC}}{{AC}}} \right)^2} = 1\\  \Rightarrow {\sin ^2}\theta  + {\cos ^2}\theta  = 1 \end{array}$$ [/tex]

যেহেতু [tex]\frac{{AB}}{{AC}} = \sin \theta [/tex] এবং [tex]\frac{{BC}}{{AC}} = \cos \theta [/tex]

অতএব আমরা বলতে পারি 

[tex] $$\begin{array}{l} {\sin ^2}\theta  = 1 - {\cos ^2}\theta \\  \Rightarrow \sin \theta  = \sqrt {1 - {{\cos }^2}\theta }  \end{array}$$ [/tex]

অনুরূপে 

[tex] $$\begin{array}{l} {\cos ^2}\theta  = 1 - {\sin ^2}\theta \\  \Rightarrow \cos \theta  = \sqrt {1 - {{\sin }^2}\theta }  \end{array}$$ [/tex]

(2)  আবার চিত্রে সমকোণী ত্রিভুজ ABC থেকে পাই ,

[tex]A{C^2} = A{B^2} + B{C^2}[/tex]

এই সম্পর্কের উভয়পাশে [tex]B{C^2}[/tex] দিয়ে ভাগ করে পাই 

[tex] $$\begin{array}{l} \frac{{A{C^2}}}{{B{C^2}}} = \frac{{A{B^2} + B{C^2}}}{{B{C^2}}}\\  \Rightarrow {\left( {\frac{{AC}}{{BC}}} \right)^2} = {\left( {\frac{{AB}}{{BC}}} \right)^2} + 1\\  \Rightarrow {\sec ^2}\theta  = {\tan ^2}\theta  + 1 \end{array}$$ [/tex]

যেহেতু [tex]\frac{{AC}}{{BC}} = \sec \theta [/tex] এবং [tex]\frac{{AB}}{{BC}} = \tan \theta [/tex]

সুতরাং [tex]\sec \theta  = \sqrt {\tan \theta  + 1} [/tex]

আবার 

[tex] $$\begin{array}{l} {\tan ^2}\theta  = {\sec ^2}\theta  - 1\\  \Rightarrow \tan \theta  = \sqrt {{{\sec }^2}\theta  - 1}  \end{array}$$ [/tex]

(3) আবার চিত্রে সমকোণী ত্রিভুজ ABC থেকে পাই ,

[tex]A{C^2} = A{B^2} + B{C^2}[/tex]

এই সম্পর্কের উভয়পাশে [tex]{A{B^2}}[/tex] দিয়ে ভাগ করে পাই 

[tex] $$\begin{array}{l} \frac{{A{C^2}}}{{A{B^2}}} = \frac{{A{B^2}}}{{A{B^2}}} + \frac{{B{C^2}}}{{A{B^2}}}\\  \Rightarrow {\left( {\frac{{AC}}{{AB}}} \right)^2} = 1 + {\left( {\frac{{BC}}{{AB}}} \right)^2}\\  \Rightarrow \cos e{c^2}\theta  = 1 + {\cot ^2}\theta  \end{array}$$ [/tex]

যেহেতু [tex]\frac{{AC}}{{AB}} = \cos ec\theta [/tex] এবং [tex]\frac{{BC}}{{AB}} = \cot \theta [/tex]

সুতরাং [tex]\cos ec\theta  = \sqrt {1 + {{\cot }^2}\theta } [/tex]

আবার 

[tex] $$\begin{array}{l} {\cot ^2}\theta  = \cos e{c^2}\theta  - 1\\  \Rightarrow \cot \theta  = \sqrt {\cos e{c^2}\theta  - 1}  \end{array}$$ [/tex]

ত্রিকোণমিতিক অনুপাতগুলির পারস্পরিক সম্পর্কের বিস্তারিত আলোচনা থেকে দেখতে পাওয়া যায় যে , কোনো একটি কোণের যেকোনো একটি কোণানুপাত দেওয়া থাকলে তা থেকে অন্যান্য কোণানুপাতগুলি নির্ণয় করা যায়। 

 

নিচের ছকে ত্রিকোণমিতিক অনুপাতগুলির পারস্পরিক সম্পর্ক দেওয়া হল 

 

	[tex]\sin \theta [/tex]	[tex]\cos \theta [/tex]	[tex]\tan \theta [/tex]	[tex]\cot \theta [/tex]	[tex]\sec \theta [/tex]	[tex]\cos ec\theta [/tex]
[tex]\sin \theta [/tex]	[tex]\sin \theta [/tex]	[tex]\sqrt {1 - {{\cos }^2}\theta } [/tex]	[tex]\frac{{\tan \theta }}{{\sqrt {1 + {{\tan }^2}\theta } }}[/tex]	[tex]\frac{1}{{\sqrt {1 + {{\cot }^2}\theta } }}[/tex]	[tex]\frac{{\sqrt {{{\sec }^2}\theta  - 1} }}{{\sec \theta }}[/tex]	[tex]\frac{1}{{\cos ec\theta }}[/tex]
[tex]\cos \theta [/tex]	[tex]\sqrt {1 - {{\sin }^2}\theta } [/tex]	[tex]\cos \theta [/tex]	[tex]\frac{1}{{\sqrt {1 + {{\tan }^2}\theta } }}[/tex]	[tex]\frac{{\cot \theta }}{{\sqrt {1 + {{\cot }^2}\theta } }}[/tex]	[tex]\frac{1}{{\sec \theta }}[/tex]	[tex]\frac{{\sqrt {\cos e{c^2}\theta  - 1} }}{{\cos ec\theta }}[/tex]
[tex]\tan \theta [/tex]	[tex]\frac{{\sin \theta }}{{\sqrt {1 - {{\sin }^2}\theta } }}[/tex]	[tex]\frac{{\sqrt {1 - {{\cos }^2}\theta } }}{{\cos \theta }}[/tex]	[tex]\tan \theta [/tex]	[tex]\frac{1}{{\cot \theta }}[/tex]	[tex]\sqrt {{{\sec }^2}\theta  - 1} [/tex]	[tex]\frac{1}{{\sqrt {\cos e{c^2}\theta  - 1} }}[/tex]
[tex]\cot \theta [/tex]	[tex]\frac{{\sqrt {1 - {{\sin }^2}\theta } }}{{\sin \theta }}[/tex]	[tex]\frac{{\cos \theta }}{{\sqrt {1 - {{\cos }^2}\theta } }}[/tex]	[tex]\frac{1}{{\tan \theta }}[/tex]	[tex]\cot \theta [/tex]	[tex]\frac{1}{{\sqrt {{{\sec }^2}\theta  - 1} }}[/tex]	[tex]\sqrt {\cos e{c^2}\theta  - 1} [/tex]
[tex]\sec \theta [/tex]	[tex]\frac{1}{{\sqrt {1 - {{\sin }^2}\theta } }}[/tex]	[tex]\frac{1}{{\cos \theta }}[/tex]	[tex]\sqrt {1 + {{\tan }^2}\theta } [/tex]	[tex]\frac{{\sqrt {1 + {{\cot }^2}\theta } }}{{\cot \theta }}[/tex]	[tex]\sec \theta [/tex]	[tex]\frac{{\cos ec\theta }}{{\sqrt {\cos e{c^2}\theta  - 1} }}[/tex]
[tex]\cos ec\theta [/tex]	[tex]\frac{1}{{\sin \theta }}[/tex]	[tex]\frac{1}{{\sqrt {1 - {{\cos }^2}\theta } }}[/tex]	[tex]\frac{{\sqrt {1 + {{\tan }^2}\theta } }}{{\tan \theta }}[/tex]	[tex]{\sqrt {1 + {{\cot }^2}\theta } }[/tex]	[tex]\frac{{\sec \theta }}{{\sqrt {{{\sec }^2}\theta  - 1} }}[/tex]	[tex]\cos ec\theta [/tex]

 

কয়েকটি কোণের ত্রিকোণমিতিক অনুপাতের মান 

আগের আলোচনায় আমরা দেখেছি দুই বা ততোধিক সদৃশ সমকোণী ত্রিভুজের বাহুগুলির দৈর্ঘ্য যাই হোক না কেন তাদের যেকোনো একটি অনুরূপ সূক্ষকোণের পরিপ্রেক্ষিতে ত্রিকোণমিতিক অনুপাতের মান অপরিবর্তিত থাকে। নীচে ত্রিভুজ ABC এবং ত্রিভুজ DEF দুটি সদৃশ সমকোণী ত্রিভুজ , যাদের [tex]\angle ABC = \angle DEF = \theta [/tex] . 

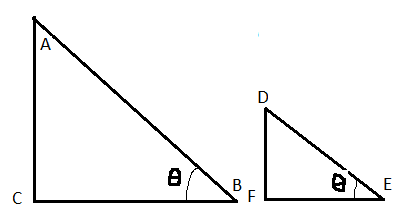
লক্ষ্য করলেই দেখা যাচ্ছে তাদের বাহুগুলি সমান নয়। কিন্তু আমরা জানি [tex]\frac{{AC}}{{AB}} = \frac{{DF}}{{DE}}[/tex] অর্থাৎ [tex]\sin \angle ABC = \sin \angle DEF = \sin \theta [/tex] এবং [tex]\frac{{AC}}{{BC}} = \frac{{DF}}{{EF}}[/tex] অর্থাৎ [tex]\tan \angle ABC = \tan \angle DEF = \tan \theta [/tex] . অনুরূপভাবে ত্রিকোণমিতিক অনুপাত গুলির সমতা দেখানো যায়। 

এ থেকে বোঝাযায় যে জ্যামিতিক অঙ্কনের সাহায্যে একটি সমকোণী ত্রিভুজের মধ্যে যেকোনো পরিমাপের সূক্ষকোণ নিয়ে তার ত্রিকোণমিতিক অনুপাতগুলির মান নির্ণয় করা যায়। 

 

কয়েকটি আদর্শ কোণের ত্রিকোণমিতিক অনুপাতের মান নির্ণয় 

[tex]{0^ \circ }[/tex] থেকে [tex]{90^ \circ }[/tex] পর্যন্ত , এর মধ্যে এমন কয়েকটি কোণ আছে যাদের কোণানুপাতের মান কোনো প্রকার মাপ যোগের ঝামেলা না করেই জ্যামিতিক তত্ত্বের সাহায্যে নির্ণয় করা যায়। সেই কোণ গুলি হল [tex]{0^ \circ }[/tex] , [tex]{30^ \circ }[/tex] , [tex]{45^ \circ }[/tex] , [tex]{60^ \circ }[/tex] , [tex]{90^ \circ }[/tex] . ত্রিকোনমিতিতে এই সমস্ত কোণ গুলিকে আদর্শ কোণ বলে। নীচে আদর্শ কোণের মান নির্ণয় পদ্ধতি দেওয়া হল। 

[tex]{45^ \circ }[/tex] কোণের ত্রিকোণমিতিক অনুপাতের মান নির্ণয় 

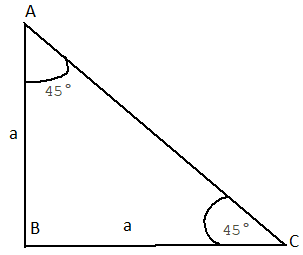
উপরের চিত্রে ABC হল সমকোণী ত্রিভুজ , যার [tex]\angle BAC = {45^ \circ }[/tex] ; এই ত্রিকোণমিতিক অনুপাতগুলির মান নির্ণয় করতে হবে।

  যেহেতু [tex]\angle BAC = {45^ \circ }[/tex] , অতএব [tex]\angle BCA = {45^ \circ }[/tex] হবে।

সুতরাং BC = AB .

এখন মনে করি BC = AB = a .

আমরা জানি অতিভুজ [tex]CA = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{a^2} + {a^2}}  = a\sqrt 2 [/tex]

এখন অতিভুজ [tex]CA = a\sqrt 2 [/tex] , লম্ব AB = a এবং ভূমি BC = a 

সুতরাং [tex]\sin {45^ \circ } = \frac{{AB}}{{CA}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }}[/tex]

[tex]\cos ec{45^ \circ } = \frac{{CA}}{{AB}} = \frac{{a\sqrt 2 }}{a} = \sqrt 2 [/tex]

[tex]\cos {45^ \circ } = \frac{{BC}}{{CA}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }}[/tex]

[tex]sec{45^ \circ } = \frac{{CA}}{{BC}} = \frac{{a\sqrt 2 }}{a} = \sqrt 2 [/tex]

[tex]\tan {45^ \circ } = \frac{{AB}}{{BC}} = \frac{a}{a} = 1[/tex]

[tex]\cot {45^ \circ } = \frac{{BC}}{{AB}} = \frac{a}{a} = 1[/tex]

 

[tex]{60^ \circ }[/tex] কোণের ত্রিকোণমিতিক অনুপাতের মান 

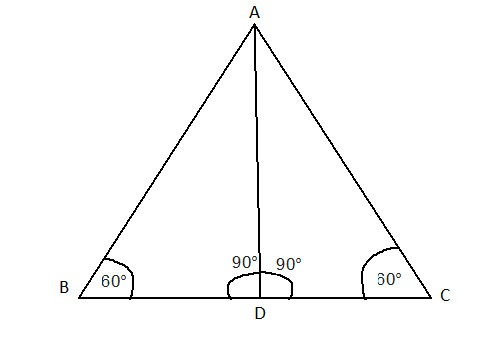
উপরের চিত্রে ABD হল একটি সমকোণী ত্রিভুজ। যার [tex]\angle ABD = {60^ \circ }[/tex] এই কোণের ত্রিকোণমিতিক মান নির্ণয় করতে হবে। 

অঙ্কন : BD কে C পর্যন্ত এমন ভাবে বাড়ানো হল যেন BD = DC হয়। A , C কে যুক্ত করা হল।

এখন ত্রিভুজ ABD এবং ত্রিভুজ ACD এর মধ্যে BD = DC , AB হল সাধারণ এবং [tex]\angle ADB = \angle ADC[/tex] ( উভয়েই সমকোণ ) . অতএব ত্রিভুজ দুটি সর্বসম। 

সুতরাং [tex]\angle ABD = {60^ \circ } = \angle ACD[/tex] এবং ত্রিভুজ ABC হল সমবাহু ত্রিভুজ। 

এবার মনে করি AB = 2a 

অতএব AC = 2a . BD = a = CD 

ত্রিভুজ ABD তে 

[tex] $$\begin{array}{l} AD\\  = \sqrt {A{B^2} - B{D^2}} \\  = \sqrt {4{a^2} - {a^2}} \\  = \sqrt {3{a^2}} \\  = a\sqrt 3  \end{array}$$ [/tex]

তাহলে ত্রিভুজ ABD তে [tex]\angle ABD[/tex] এর পরিপ্রেক্ষিতে 

অতিভুজ AB = 2a , লম্ব [tex]AD = a\sqrt 3 [/tex] এবং ভূমি BD = a 

সুতরাং [tex]\sin {60^ \circ } = \frac{{AD}}{{AB}} = \frac{{a\sqrt 3 }}{{2a}} = \frac{{\sqrt 3 }}{2}[/tex]

[tex]\cos ec{60^ \circ } = \frac{{AB}}{{AD}} = \frac{{2a}}{{a\sqrt 3 }} = \frac{2}{{\sqrt 3 }}[/tex]

[tex]\cos {60^ \circ } = \frac{{BD}}{{AB}} = \frac{a}{{2a}} = \frac{1}{2}[/tex]

[tex]\sec {60^ \circ } = \frac{{AB}}{{BD}} = \frac{{2a}}{a} = 2[/tex]

[tex]\tan {60^ \circ } = \frac{{AD}}{{BD}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 [/tex]

[tex]\cot {60^ \circ } = \frac{{BD}}{{AD}} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }}[/tex]

 

[tex]{30^ \circ }[/tex] কোণের ত্রিকোণমিতিক অনুপাতের মান 

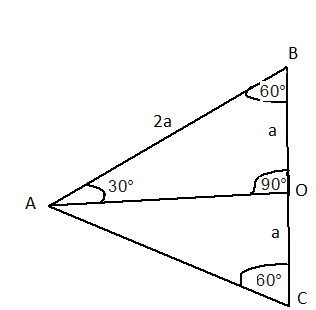
উপরের চিত্রে AOB হল একটি সমকোণী ত্রিভুজ। এই ত্রিভুজের [tex]\angle BAO = {30^ \circ }[/tex] . এই কোণের ত্রিকোণমিতিক অনুপাতগুলির মান নির্ণয় করতে হবে। 

অঙ্কন : BO কে C বিন্দু পর্যন্ত এমন ভাবে বর্ধিত করা হল , যাতে BO = OC হয় এবং AC যুক্ত করা হল।

এখন ত্রিভুজ AOB এবং ত্রিভুজ AOC এর মধ্যে BO =OC , AD সাধারণ বাহু এবং [tex]\angle AOB = \angle AOC[/tex] ( উভয়ই সমকোণ ) . 

অতএব ত্রিভুজ দুটি সর্বসম। সুতরাং আমরা বলতে পারি [tex]\angle ABO = \angle ACO = {60^ \circ }[/tex] এবং [tex]\angle OAB = \angle OAC = {30^ \circ }[/tex] .অতএব ত্রিভুজ ABC হল সমবাহু ত্রিভুজ। 

মনে করি AB = 2a = AC এবং OB = OC = a .

অতএব সমকোণী ত্রিভুজ AOB এর 

[tex] $$\begin{array}{l} AO\\  = \sqrt {A{B^2} - B{O^2}} \\  = \sqrt {4{a^2} - {a^2}} \\  = a\sqrt 3  \end{array}$$ [/tex]

এখন সমকোণী ত্রিভুজ AOB এর [tex]\angle BAO[/tex] এর সাপেক্ষে অতিভুজ AB = 2a , লম্ব OB = a এবং ভূমি OA = [tex]a\sqrt 3 [/tex]

এখন [tex]\sin {30^ \circ } = \frac{{OB}}{{AB}} = \frac{a}{{2a}} = \frac{1}{2}[/tex]

[tex]\cos ec{30^ \circ } = \frac{{AB}}{{OB}} = \frac{{2a}}{a} = 2[/tex]

[tex]\cos {30^ \circ } = \frac{{AO}}{{AB}} = \frac{{a\sqrt 3 }}{{2a}} = \frac{{\sqrt 3 }}{2}[/tex]

[tex]\sec {30^ \circ } = \frac{{AB}}{{OA}} = \frac{{2a}}{{a\sqrt 3 }} = \frac{2}{{\sqrt 3 }}[/tex]

[tex]\tan {30^ \circ } = \frac{{OB}}{{OA}} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }}[/tex]

[tex]\cot {30^ \circ } = \frac{{OA}}{{OB}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 [/tex]

 

[tex]{90^ \circ }[/tex] কোণের ত্রিকোণমিতিক অনুপাতের মান 

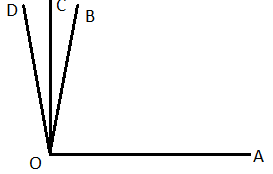
এখানে আমরা এমন একটা অবস্থানের কথা ভাবছি যখন ঘূর্ণিয়মান রেখাটি একটি সমকোণ অর্থাৎ [tex]{90^ \circ }[/tex] কোণ উৎপন্ন করবে , এবং তার যেকোন এক বিন্দু থেকে মূল বাহুর উপর লম্ব টেনে একটি সমকোণী ত্রিভুজ পাওয়া যাবে। উপরের চিত্রে দেখা যাচ্ছে , ঘূর্ণিয়মান রেখাটি যতই [tex]{90^ \circ }[/tex] এর কাছাকাছি যাচ্ছে ততই তার থেকে অঙ্কিত লম্ব সমকোণী ত্রিভুজের অতিভুজের সাথে মিলে যাচ্ছে এবং ত্রিভুজের ভূমির দৈর্ঘ্য কমে যাচ্ছে। এ অবস্থায় ঘূর্ণিয়মান রেখাটি যখন ঠিক [tex]{90^ \circ }[/tex] কোণ উৎপন্ন করবে তখন অতিভুজ এবং লম্ব একটি রেখায় পরিণত হয় অর্থাৎ প্রয়োজনীয় ত্রিভুজটির অস্তিত্ব থাকবেনা ( কারণ একটি সমকোণী ত্রিভুজের একটিই সমকোণ থাকতে পারে। ) সুতরাং এক্ষেত্রে নীচের ত্রিকোণমিতিক অনুপাতের মান গুলি হবে। 

[tex] $$\begin{array}{l} \sin {90^ \circ } = 1\\ \cos ec{90^ \circ } = 1\\ \cos {90^ \circ } = 0\\ \cot {90^ \circ } = 0 \end{array}$$ [/tex]

মন্তব্য [tex]\sec {90^ \circ }[/tex] এবং [tex]\tan {90^ \circ }[/tex] এর মান অসংজ্ঞাত। 

 

[tex]{0^ \circ }[/tex] কোণের ত্রিকোণমিতিক অনুপাতের মান 

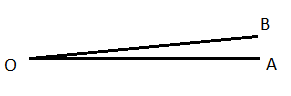
এখানে আমরা এমন একটি অবস্থার কথা ভাবছি যখন ঘূর্ণিয়মান রেখাটি তার যাত্রা শুরু করেছে , কিন্তু মূল অবস্থান ছেড়ে সে নতুন কোনো অবস্থানে যায়নি। এই অবস্থায় আমরা বলি ঘূর্ণিয়মান রেখাটি [tex]{0^ \circ }[/tex] কোণ উৎপন্ন করেছে। এ অবস্থায় ভূমি ও অতিভুজ একে অন্যটির উপর মিলিত হয় অর্থাৎ তারা একটি রেখায় পরিণত হয়। এক্ষেত্রে একটি লম্ব টেনে সমকোণী ত্রিভুজ পাওয়া যায় না। ( কারণ কোনো ত্রিভুজের একটি কোণ [tex]{0^ \circ }[/tex] হতে পারে না। ) সুতরাং এই ক্ষেত্রেও নীচের ত্রিকোণমিতিক অনুপাতের মানগুলির সংজ্ঞা হিসাবে ধরা হয়। 

[tex] $$\begin{array}{l} \sin {0^ \circ } = 0\\ \cos {0^ \circ } = 1\\ \tan {0^ \circ } = 0\\ \sec {0^ \circ } = 1 \end{array}$$ [/tex]

মন্তব্য [tex]\cos ec{0^ \circ }[/tex] এবং [tex]\cot {0^ \circ }[/tex] এর মান অসংজ্ঞাত। 

 

আদর্শ কোণের ত্রিকোণমিতিক মানে তালিকা 

কোণানুপাত	[tex]{0^ \circ }[/tex]	[tex]{30^ \circ }[/tex] বা [tex]\frac{\pi }{6}[/tex]	[tex]{45^ \circ }[/tex] বা [tex]\frac{\pi }{4}[/tex]	[tex]{60^ \circ }[/tex] বা [tex]\frac{\pi }{3}[/tex]	[tex]{90^ \circ }[/tex] বা [tex]\frac{\pi }{2}[/tex]
[tex]\sin [/tex]	0	[tex]\frac{1}{2}[/tex]	[tex]\frac{1}{{\sqrt 2 }}[/tex]	[tex]\frac{{\sqrt 3 }}{2}[/tex]	1
[tex]\cos [/tex]	1	[tex]\frac{{\sqrt 3 }}{2}[/tex]	[tex]\frac{1}{{\sqrt 2 }}[/tex]	[tex]\frac{1}{2}[/tex]	0
[tex]\tan [/tex]	0	[tex]\frac{1}{{\sqrt 3 }}[/tex]	1	[tex]\sqrt 3 [/tex]	অসংজ্ঞাত
[tex]\cos ec[/tex]	অসংজ্ঞাত	2	[tex]\sqrt 2 [/tex]	[tex]\frac{2}{{\sqrt 3 }}[/tex]	1
[tex]\sec [/tex]	1	[tex]\frac{2}{{\sqrt 3 }}[/tex]	[tex]\sqrt 2 [/tex]	2	অসংজ্ঞাত
[tex]\cot [/tex]	অসংজ্ঞাত	[tex]\sqrt 3 [/tex]	1	[tex]\frac{1}{{\sqrt 3 }}[/tex]	0