কোণের পরিমাপ (Measurement of angle)
যেহেতু ত্রিকোণমিতি নামক গণিতের এই বিশেষ শাখা প্রধানত সমকোণী ত্রিভুজের সূক্ষকোণ দুটির পরিপেক্ষিতে বাহুগুলির অনুপাতের উপর প্রতিষ্ঠিত তাই প্রথমেই কোণ সম্পর্কে বিস্তারিত আলোচনার প্রয়োজন ।
কোণ কাকে বলে ? (What is angle)
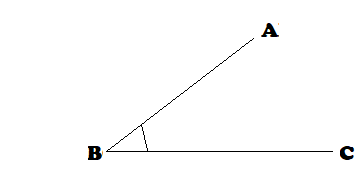 (i) দুটি রেখা একটি বিন্দুতে মিলিত হলে ওই বিন্দুতে একটি কোণ উৎপন্ন হয় । যেমন পাশের চিত্রে AB ও BC দুটি রেখা B বিন্দুতে মিলিত হয়েছে, তারফলে B বিন্দুতে ∠ABC কোণ উৎপন্ন হয়েছে । ∠ABC কে আমরা জ্যামিতিক কোণ বলি ।
(i) দুটি রেখা একটি বিন্দুতে মিলিত হলে ওই বিন্দুতে একটি কোণ উৎপন্ন হয় । যেমন পাশের চিত্রে AB ও BC দুটি রেখা B বিন্দুতে মিলিত হয়েছে, তারফলে B বিন্দুতে ∠ABC কোণ উৎপন্ন হয়েছে । ∠ABC কে আমরা জ্যামিতিক কোণ বলি ।
একটি রেখাকে তার প্রান্ত বিন্দু স্থির রেখে যদি ঘড়ির কাঁটার বিপরীতদিকে ঘোরানো হয় , তবে সেই রেখার প্রথম অবস্থানের সঙ্গে তার পরবর্তী প্রতিটি অবস্থান সেই প্রান্তবিন্দুতে এক একটি কোণ উৎপন্ন করে।
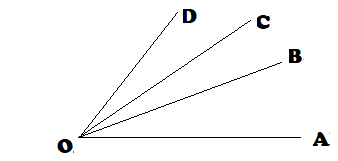 পাশের চিত্রে OA রেখাটিকে তার প্রান্তীয় বিন্দু O কে স্থির রেখে ঘড়ির কাঁটার বিপরীতদিকে ঘুরিয়ে OB, OC, OD অবস্থানে নিয়ে গেলে, প্রথম অবস্থানের সঙ্গে এই অবস্থানগুলি যথাক্রমে ∠BOA,∠COA,∠DOA কোণ উৎপন্ন করে । এই কোণ গুলিকে ত্রিকোণমিতি কোণ বলে ।
পাশের চিত্রে OA রেখাটিকে তার প্রান্তীয় বিন্দু O কে স্থির রেখে ঘড়ির কাঁটার বিপরীতদিকে ঘুরিয়ে OB, OC, OD অবস্থানে নিয়ে গেলে, প্রথম অবস্থানের সঙ্গে এই অবস্থানগুলি যথাক্রমে ∠BOA,∠COA,∠DOA কোণ উৎপন্ন করে । এই কোণ গুলিকে ত্রিকোণমিতি কোণ বলে ।
আগের আলোচনা থেকে বোঝাযাচ্ছে জ্যামিতিক কোণের পরিমাপই মূল বিচার্য বিষয় । জ্যামিতিক কোণের পরিমাপ 0∘ থেকে 360∘ পর্যন্ত যেকোনো মানের হতে পারে, কিন্তু তার চেয়ে বড়ো হতে পারেনা । অর্থাৎ ঘূর্ণিয়মান রেখাটি এক পাক ঘুরে এসে তার প্রথম অবস্থানের সঙ্গে মিশলে 360∘ কোণ উৎপন্ন হয় ।
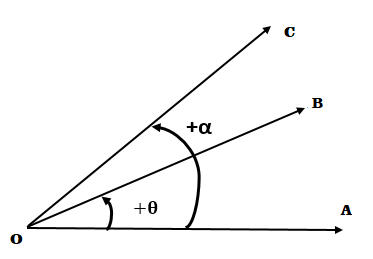 ত্রিকোণমিতির কোণের ক্ষেত্রে ঘূর্ণিয়মান রেখার দিক ও তার ফলে সৃষ্টি কোণের পরিমান উভয়ই বিচার করা হয় । ঘূর্ণিয়মান রেখাটি ঘড়ির কাঁটার বিপরীত দিকে ঘুরলে কোণ উৎপন্ন হয় তাকে ধনাত্মক কোণ (Positive angle) বলে । বিপরীতক্রমে ঘূর্ণিয়মান রেখাটি ঘড়ির কাঁটার দিকে ঘুরলে যে কোণ উৎপন্ন হয় তাকে ঋণাত্মক কোণ (Negative angle) বলে ।
ত্রিকোণমিতির কোণের ক্ষেত্রে ঘূর্ণিয়মান রেখার দিক ও তার ফলে সৃষ্টি কোণের পরিমান উভয়ই বিচার করা হয় । ঘূর্ণিয়মান রেখাটি ঘড়ির কাঁটার বিপরীত দিকে ঘুরলে কোণ উৎপন্ন হয় তাকে ধনাত্মক কোণ (Positive angle) বলে । বিপরীতক্রমে ঘূর্ণিয়মান রেখাটি ঘড়ির কাঁটার দিকে ঘুরলে যে কোণ উৎপন্ন হয় তাকে ঋণাত্মক কোণ (Negative angle) বলে ।
পাশের চিত্রে OA রেখাটি ঘড়ির কাঁটার বিপরীত দিকে ঘুরে OB এবং OC অবস্থানে গিয়ে OA রেখার সাথে O বিন্দুতে যথাক্রমে +θ∘ এবং +α∘ কোণ উৎপন্ন করেছে ।
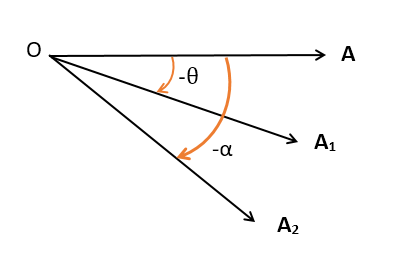
আবার ডানপাশের চিত্রে OA রেখাটি ঘড়ির কাঁটার দিকে ঘুরে A1 এবং A2 অবস্থানে গিয়ে পূর্ব অবস্থান অর্থাৎ OA অবস্থানের সঙ্গে যথাক্রমে −θ এবং −α কোণ উৎপন্ন করেছে ।
জ্যামিতিক কোণের ক্ষেত্রে রেখাটি একপাক সম্পূর্ণ ঘোরার পর আবার ঘুরতে শুরু করলে কোণের মান নতুন করে 0∘ থেকে বাড়তে শুরু করবে । তারপর একপাক সম্পূর্ণ করলে আবার 360∘ হবে। কিন্তু কোণের মান কখনই 360∘ এর বেশি হবেনা । এখানে আবার উল্লেখ করছি জ্যামিতিক কোণের ক্ষেত্রে রেখাটি ঘড়ির কাঁটার বিপরীত দিকে ঘুরছে কিনা তা বিচার্য বিষয় নয় ।
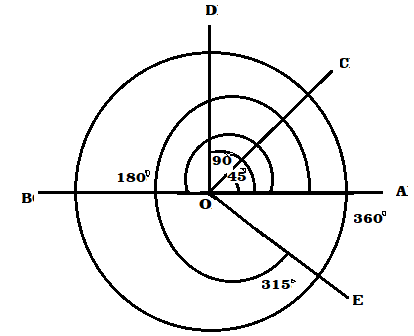
ত্রিকোণমিতিক কোণ 0∘ থেকে শুরু করে যেকোনো পরিমাপ হতে পারে, এমনকি ঋণাত্মকও । ঘূর্ণিয়মান রেখাটি ঘড়ির কাঁটার বিপরীত দিকে যতবার পাক খাবে, কোণের পরিমান ততবার 360∘ করে বেড়ে যাবে । আবার রেখাটি ঘড়ির কাঁটার দিকে যতবার পাক খাবে কোণের মান তত 360∘ করে কমে যাবে ।
কোণের পরিমাপের বিভিন্ন পদ্ধতি
কোণের পরিমাপ সাধারণত দুটি পদ্ধতিতে করা হয়
1. ষষ্ঠিক পদ্ধতি
2. বৃত্তীয় পদ্ধতি
1. ষষ্ঠিক পদ্ধতি :- এই পদ্ধতিতে ঘূর্ণিয়মান রেখাটি পুরো একপাক ঘুরে এলে যে কোণ উৎপন্ন হয় তাকে 360∘ ধরে তার চার ভাগের একভাগকে 90∘ বা এক সমকোণ ধরা হয় । এক সমকোণ বা 90∘ এর 190 অংশকে 1∘ ধরা হয়। এই পদ্ধতিতে অন্যান্য নিম্ন এককগুলি হল মিনিট ও সেকেন্ড। এদের মধ্যে সম্পর্ক নিচে দেওয়া হল
এক সমকোণ = 90∘ ( ডিগ্রি )
1∘ ( ডিগ্রি ) = 60' ( মিনিট )
1' ( মিনিট ) = 60'' ( সেকেন্ড )
2. বৃত্তীয় পদ্ধতি :- যেকোনো একটি বৃত্তের পরিধি ও বৃত্তের ব্যাসার্ধের মধ্যে যে ধ্রূবক সম্পর্কটি রয়েছে তার উপর ভিত্তি করে এই পদ্ধতির একক নির্ধারিত হয়েছে। 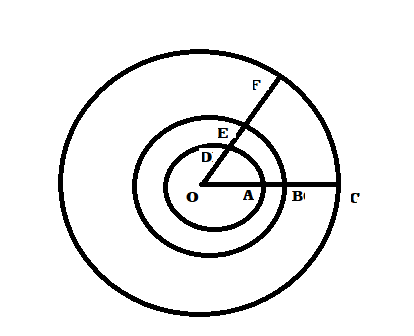 পাশের ক্ষেত্রে তিনটি এক কেন্দ্রীয় বৃত্ত রয়েছে। সবচেয়ে ছোট বৃত্তটির পরিধি থেকে বৃত্তের ব্যাসার্ধের সমান দৈঘ্যের একটি বৃত্তচাপ AD কেটে নয়া হল। এবার AO এবং AD যুক্ত করলে ∠AOD কোণ পাওয়া যাবে , যা হল বৃত্তের ব্যাসার্ধের সমান দৈর্ঘের চাপের উপরে অবস্থিত কেন্দ্রস্থ একটি কোণ ।
পাশের ক্ষেত্রে তিনটি এক কেন্দ্রীয় বৃত্ত রয়েছে। সবচেয়ে ছোট বৃত্তটির পরিধি থেকে বৃত্তের ব্যাসার্ধের সমান দৈঘ্যের একটি বৃত্তচাপ AD কেটে নয়া হল। এবার AO এবং AD যুক্ত করলে ∠AOD কোণ পাওয়া যাবে , যা হল বৃত্তের ব্যাসার্ধের সমান দৈর্ঘের চাপের উপরে অবস্থিত কেন্দ্রস্থ একটি কোণ ।
এবার OA এবং OD কে বর্ধিত করলে তা অন্য দুটি বৃত্তকে যথাক্রমে B , C এবং E , F বিন্দুতে ছেদ করবে। মেপে দেখলে দেখা যাবে দুটি বৃত্তচাপ BE এবং CF এর দৈর্ঘ্য সংশ্লিট বৃত্তের ব্যাসার্ধ্যের সমান ; অর্থাৎ ∠BOE এবং ∠COF ও সংশ্লিট বৃত্তের ব্যাসার্ধের সমান দৈঘ্যের চাপের উপরে অবস্থিত কেন্দ্রস্থ কোণ ।
এর থেকে এই সিন্ধান্ত করা যায় যেকোনো বৃত্তের ব্যাসার্ধের সমান দৈর্ঘ্যবিশিষ্ট চাপ সবসময় কেন্দ্রে একটি নিদিষ্ট পরিমান কোণ ধারণ করে। এই কোণের পরিমানকেই বৃত্তীয় পদ্ধতিতে একক ধরা হয় এবং তাকে এক রেডিয়ান বলা হয়। ইহাকে প্রকাশ করা হয় 1c চিহ্নের সাহায্যে ।
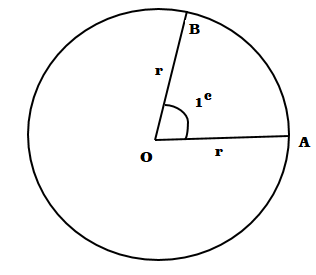 রেডিয়ান একটি ধ্রূবক কোণ :- মনে করি O হল একটি বৃত্তের কেন্দ্র এবং তার ব্যাসার্ধ OA = r ; OA ব্যাসার্ধের সমান একটি চাপ AB নিলে সংজ্ঞানুসারে ∠AOB=1 রেডিয়ান। এখন OA রেখাটিকে বর্ধিত করলে রেখাটি বৃত্তের C বিন্দুতে ছেদ করে। তাহলে ABC চাপ বৃত্ত পরিধির অর্ধেক এবং সেই চাপ দ্বারা ধৃত কেন্দ্রস্থ কোণ
রেডিয়ান একটি ধ্রূবক কোণ :- মনে করি O হল একটি বৃত্তের কেন্দ্র এবং তার ব্যাসার্ধ OA = r ; OA ব্যাসার্ধের সমান একটি চাপ AB নিলে সংজ্ঞানুসারে ∠AOB=1 রেডিয়ান। এখন OA রেখাটিকে বর্ধিত করলে রেখাটি বৃত্তের C বিন্দুতে ছেদ করে। তাহলে ABC চাপ বৃত্ত পরিধির অর্ধেক এবং সেই চাপ দ্বারা ধৃত কেন্দ্রস্থ কোণ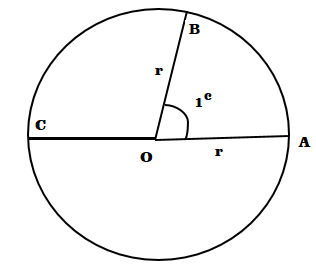 ∠AOC= এক সরলকোণ = দুই সমকোণ।
∠AOC= এক সরলকোণ = দুই সমকোণ।
এখন উপরের দুটি চাপ এবং দুটি কোণের অনুপাত করলে আমরা পাই
![]() =r12×2πr=1π
=r12×2πr=1π
এবং ∠AOB∠AOC=1c2⊥
এখানে ⊥=1সমকোণ। কিন্তু জ্যামিতিতে দেখা যায় যেকোনো বৃত্তে বিভিন্ন চাপের দ্বারা ধৃত কেন্দ্রস্থ কোণগুলির অনুপাত সেই সব চাপের দৈর্ঘ্যের অনুপাতের সমান। সুতরাং
![]() =∠AOB∠AOC
=∠AOB∠AOC
অতএব 1c2⊥=1π
অতএব 1 রেডিয়ান = 1π×2 সমকোণ এবং এই মানটি একটি ধ্রূবক সংখ্যা কারণ 2 সমকোণ এবং π উভয়েই ধ্রূবক। গণনার সুবিধার জন্য π এর আসন্ন মান 227 নেওয়া হয় ।
পদ্ধতি দুটির এককবলির সম্পর্ক
| ষষ্ঠিক পদ্ধতি | বৃত্তীয় পদ্ধতি |
|---|---|
| 360∘ | 2πc |
| 180∘ | πc |
| 90∘ | πc2 |
- 11323 views