যে কোনো কোণ ও সংযুক্ত কোণসমূহের কোণানুপাত ( Trigonometrical Ratios of Any Angle and Associated Angles)
সূচনা (Introduction)
এর আগের অধ্যায়ে আমরা সূক্ষকোণের ত্রিকোণমিতিক কোণানুপাত সম্পর্কে আলোচনা করেছি। এই অধ্যায়ে যেকোনো কোণের ( ধনাত্মক বা ঋণাত্মক ) কোণানুপাতের সংজ্ঞা সম্পর্কে আলোচনা করব। তারপর একটি নির্দিষ্ট কোণ [tex]\theta [/tex] এর সঙ্গে সংশ্লিষ্ট কোণ সমূহের কোণানুপাত সম্পর্কে আলোচনা করব ।
চিহ্ন সংক্রান্ত নিয়মাবলী (Rules Regarding Signs)
মনে করি একটি সমতল পৃষ্ঠে O একটি নির্দিষ্ট বিন্দু । তাহলে O বিন্দুর মধ্যে দিয়ে অঙ্কিত XOX' ও YOY' লম্ব রেখা দুটি সমতল পৃষ্ঠকে চারটি পদে ভাগ করবে । প্রচলিত প্রথা অনুযায়ী O বিন্দু থেকে OX দিক বরাবর দূরত্ব ধনাত্মক এবং OX' দিক বরাবর দূরত্ব হল ঋণাত্মক ধরা হয় । একই ভাবে O বিন্দু থেকে OY দিক বরাবর দূরত্ব ধনাত্মক এবং OY' দিক বরাবর দূরত্ব হল ঋণাত্মক ধরা হয় । এখন মনে করি OA একটি ঘূর্ণিয়মান সরলরেখা O বিন্দুকে কেন্দ্র করে আবর্তন করে । মনে করি এখন OA সরলরেখা OX থেকে OA অবস্থানে এসে OX এর সাথে [tex]\theta [/tex] কোণ উৎপন্ন করেছে অর্থাৎ [tex]\angle XOA = \theta [/tex] .
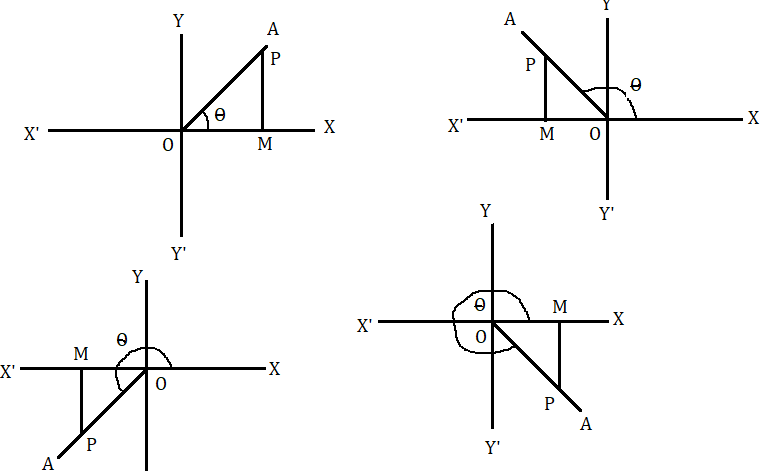
[tex]\theta [/tex] এর মান অনুযায়ী অন্তিম বহু OA এর অবস্থান প্রথম, দ্বিতীয়, তৃতীয় বা চতুর্থ পদে হতে পারে । OA বাহুর উপর যেকোনো বিন্দু P নেওয়া হল । OX এর উপর P বিন্দু থেকে PM লম্ব টানা হল । এখন নীচে OPM ত্রিভুজের বাহুগুলির চিহ্ন উল্লেখ করা হল ।
- OM ধনাত্মক হবে যদি O বিন্দু থেকে OX অভিমুখে তা মাপা হয় ।
- OM ঋণাত্মক হবে যদি O বিন্দু থেকে OX' অভিমুখে তা মাপা হয় ।
- MP ধনাত্মক হবে যদি O বিন্দু থেকে OY অভিমুখে তা মাপা হয় ।
- MP ঋণাত্মক হবে যদি O বিন্দু থেকে OY' অভিমুখে তা মাপা হয় ।
- OP এর মান সব অবস্থানে ধনাত্মক হবে ।
যেকোনো কোণের কোণানুপাত (Trigonometrical Ratios of Any Angles)
মনে করি ঘূর্ণিয়মান সরলরেখা OA, O বিন্দুকে কেন্দ্র করে আবর্তন করে (ঘড়ির কাঁটার অভিমুখে বা তার বিপরীত দিকে) এবং প্রাথমিক অবস্থান OX থেকে OA অবস্থানে এসে [tex]\angle XOA = \theta [/tex] কোণ উৎপন্ন করে । OA এর উপর যেকোনো বিন্দু P নেওয়া হল এবং OX এর উপর PM লম্ব টানা হল । এখন সমকোণী ত্রিভুজ OPM এবং বাহুগুলির অনুপাতের দ্বারা [tex]\theta [/tex] কোণের কোণানুপাতের সংজ্ঞা হয়
[tex]\sin \theta = \frac{{MP}}{{OP}}[/tex] , [tex]\cos ec\theta = \frac{{OP}}{{MP}}[/tex] ,
[tex]\cos \theta = \frac{{OM}}{{OP}}[/tex] , [tex]sec\theta = \frac{{OP}}{{OM}}[/tex]
[tex]\tan \theta = \frac{{MP}}{{OM}}[/tex] , [tex]\cot \theta = \frac{{OM}}{{MP}}[/tex]
কোণানুপাতের চিহ্ন (Sign of Trigonometrical Ratios)
উপরের আলোচনা থেকে দেখা যাচ্ছে [tex]\theta [/tex] এর মান অনুযায়ী অন্তিম বাহু প্রথম, দ্বিতীয়, তৃতীয় বা চতুর্থ যেকোনো পাদে থাকতে পারে ।
প্রথমত : মনে করি অন্তিম বাহু OA প্রথম পাদে অবস্থিত এক্ষেত্রে প্রদত্ত চিহ্নের নিয়মাবলী থেকে পাই OM ধনাত্মক, MP ধনাত্মক এবং OP ধনাত্মক ।
সুতরাং প্রদত্ত কোণ সমূহের সংজ্ঞা থেকে দেখা যায় সব কোনের মান ধনাত্মক ।
দ্বিতীয়ত : মনে করি অন্তিম বাহু OA দ্বিতীয় পাদে অবস্থিত । এক্ষেত্রে প্রদত্ত চিহ্নের নিয়মাবলী থেকে পাই OM ঋণাত্মক, MP ধনাত্মক এবং OP ধনাত্মক ।
সুতরাং প্রদত্ত কোণ সমূহের সংজ্ঞা থেকে দেখা যায় [tex]\sin \theta [/tex] ও [tex]\cos ec\theta [/tex] এর মান ধনাত্মক ও অন্যান্য কোণানুপাতের মান ঋণাত্মক ।
তৃতীয়ত : মনে করি অন্তিম বাহু OA তৃতীয় পাদে অবস্থিত এক্ষেত্রে প্রদত্ত চিহ্নের নিয়মাবলী থেকে পাই OM ঋণাত্মক, MP ঋণাত্মক এবং OP ধনাত্মক ।
সুতরাং প্রদত্ত কোণ সমূহের সংজ্ঞা থেকে দেখা যায় [tex]\tan \theta [/tex] ও [tex]\cot \theta [/tex] এর মান ধনাত্মক ও অন্যান্য কোণানুপাতের মান ঋণাত্মক ।
চতুর্থত : মনে করি অন্তিম বাহু OA চথুর্ত পাদে অবস্থিত এক্ষেত্রে প্রদত্ত চিহ্নের নিয়মাবলী থেকে পাই OM ধনাত্মক, MP ঋণাত্মক এবং OP ধনাত্মক ।
সুতরাং প্রদত্ত কোণ সমূহের সংজ্ঞা থেকে দেখা যায় [tex]\cos \theta [/tex] ও [tex]sec\theta [/tex] এর মান ধনাত্মক ও অন্যান্য কোণানুপাতের মান ঋণাত্মক ।
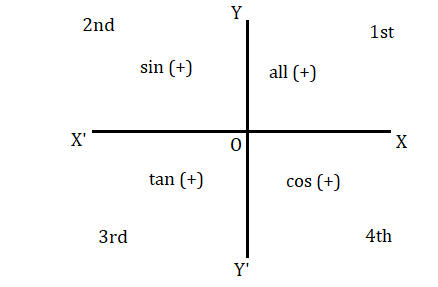
ওপরের আলোচনা থেকে আমরা পাই [tex]\theta [/tex] এর মান প্রথম পাদে হলে [tex]\theta [/tex] কোণের সব কোণানুপাত ধনাত্মক হবে ।
[tex]\theta [/tex] এর মান দ্বিতীয় পাদে হলে কেবল [tex]\sin \theta [/tex] ও [tex]\cos ec\theta [/tex] এর মান ধনাত্মক হবে।
[tex]\theta [/tex] এর মান তৃতীয় পাদে হলে কেবল [tex]\tan \theta [/tex] ও [tex]\cot \theta [/tex] এর মান ধনাত্মক হবে।
[tex]\theta [/tex] এর মান চতুর্থ পাদে হলে কেবল [tex]\cos \theta [/tex] ও [tex]sec\theta [/tex] এর মান ধনাত্মক হবে।
প্রদত্ত কোণ [tex]\theta [/tex] এর সঙ্গে সংশ্লিষ্ট কোণ সমূহের কোণানুপাত ( Trigonometrical Ratios of Angles Associated with এ given angle [tex]\theta [/tex] )
(১) [tex] - \theta [/tex] কোণের কোণানুপাত ( Trigonometrical ratios of [tex] - \theta [/tex] )
মনে করি ঘূর্ণিয়মান কোনো সরলরেখা OA , O বিন্দুকে কেন্দ্র করে ঘড়ির কাঁটার বিপরীতদিকে আবর্তন করে এবং প্রাথমিক অবস্থান OX থেকে OA অবস্থানে এসে [tex]\angle XOA = \theta [/tex] উৎপন্ন করে। আবার মনে করি OA সরলরেখাটি ঘড়ির কাঁটার দিকে আবর্তন করে প্রাথমিক অবস্থান OX থেকে OB অবস্থানে এসে [tex]\angle XOA[/tex] এর সমান [tex]\angle XOB[/tex] উৎপন্ন করে। তাহলে [tex]\angle XOB = - \theta [/tex] হবে।
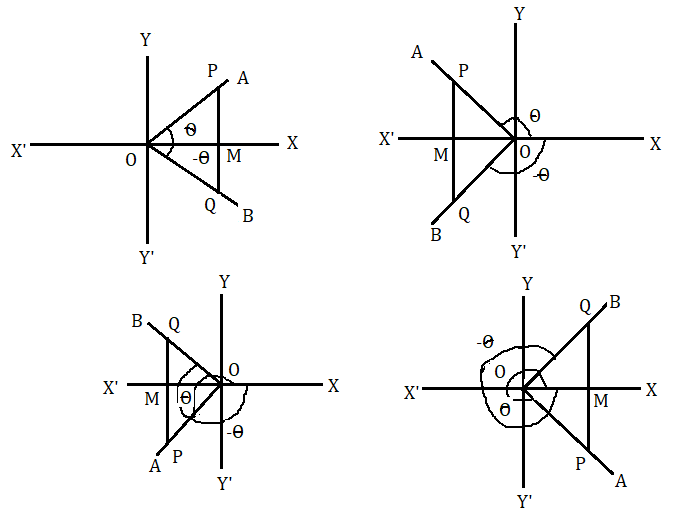
OA এর উপরে যেকোনো বিন্দু P নেওয়া হল এবং OX এর উপরে PM লম্ব টানা হল অথবা PM OX' এর উপর লম্ব টানা হল। মনে করি PM এর বর্ধিত OB কে Q বিন্দুতে ছেদ করেছে। এখন OPM ও OQM ত্রিভুজ দুটিতে [tex]\angle POM = \angle QOM[/tex] ( সংখ্যমানে ) , [tex]\angle OMP = \angle OMQ[/tex] এবং OM সাধারণ বাহু। অতএব OPM ও OQM ত্রিভুজ দুটি সর্বসম।
অতএব [tex]\overline {PM} = - \overline {QM} [/tex] এবং OP = OQ
এখন সংজ্ঞা অনুযায়ী
[tex]\sin \left( { - \theta } \right) = \frac{{\overline {QM} }}{{\overline {OQ} }} = \frac{{ - \overline {PM} }}{{\overline {OP} }} = - \sin \theta [/tex]
[tex]\cos \left( { - \theta } \right) = \frac{{\overline {OM} }}{{\overline {OQ} }} = \frac{{\overline {OM} }}{{\overline {OP} }} = \cos \theta [/tex]
[tex]\tan \left( { - \theta } \right) = \frac{{\overline {QM} }}{{\overline {OM} }} = \frac{{ - \overline {PM} }}{{\overline {OM} }} = - \tan \theta [/tex]
[tex]\cos ec\left( { - \theta } \right) = \frac{{\overline {OQ} }}{{\overline {QM} }} = \frac{{\overline {OP} }}{{ - \overline {PM} }} - \cos ec\theta [/tex]
[tex]\sec \left( { - \theta } \right) = \frac{{\overline {OQ} }}{{\overline {OM} }} = \frac{{\overline {OP} }}{{\overline {OM} }} = \sec \theta [/tex]
[tex]\cot \left( { - \theta } \right) = \frac{{\overline {OM} }}{{\overline {QM} }} = \frac{{\overline {OM} }}{{ - \overline {PM} }} = - \cot \theta [/tex]
(২) [tex]\left( {{{90}^ \circ } - \theta } \right)[/tex] কোণের কোণানুপাত ( Trigonometrical ratios of [tex]\left( {{{90}^ \circ } - \theta } \right)[/tex] )
মনে করি ঘূর্ণিয়মান কোনো সরলরেখা OA , O বিন্দুকে কেন্দ্র করে ঘড়ির কাঁটার বিপরীতদিকে আবর্তন করে এবং প্রাথমিক অবস্থান OX থেকে OA অবস্থানে এসে [tex]\angle XOA = \theta [/tex] উৎপন্ন করে। OA এর উপরে যেকোনো বিন্দু P নেওয়া হল এবং OX এর উপরে PM লম্ব টানা হল। এখন মনে করি অন্য একটি ঘূর্ণিয়মান সরলরেখা OB ঘড়ির কাটার বিপরীত দিকে আবর্তন করে এবং OX অবস্থান থেকে OY অবস্থানে এসে [tex]\angle XOY = {90^ \circ }[/tex] কোণ উৎপন্ন করে। তারপর রেখাটি ঘড়ির কাটার দিকে আবর্তন করে OY অবস্থান থেকে OB অবস্থানে এসে [tex]\angle YOB = \theta [/tex] কোণ উৎপন্ন করে। স্পষ্টতই [tex]\angle XOB = {90^ \circ } - \theta [/tex] হবে।
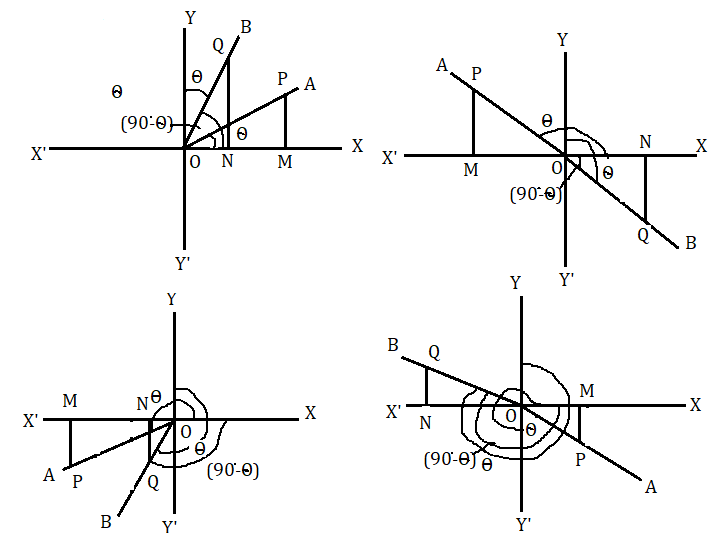
OB সরলরেখার উপরে Q বিন্দু এমন ভাবে নেওয়া হল যাতে OP = OQ হয় এবং [tex]QN \bot OX[/tex] .
যেহেতু [tex]\angle YOB = \angle XOA[/tex] সুতরাং [tex]\angle OQN = \angle POM[/tex]
এখন QON ও OPM হল সমকোণী ত্রিভুজ দুটিতে [tex]\angle OQN = \angle POM[/tex] এবং OQ = OP
সুতরাং ত্রিভুজ দুটি সর্বসম।
অতএব [tex]\overline{NQ} = \overline {OM} [/tex] [tex]\overline {ON} = \overline {MP} [/tex] [tex]\overline {OQ} = \overline {OP} [/tex]
সুতরাং সংজ্ঞানুযায়ী
[tex]\left( {{{90}^ \circ } - \theta } \right) = \frac{{\overline {NQ} }}{{\overline {OQ} }} = \frac{{\overline {OM} }}{{\overline {OP} }} = \cos \theta [/tex]
[tex]\left( {{{90}^ \circ } - \theta } \right) = \frac{{\overline {ON} }}{{\overline {OQ} }} = \frac{{\overline {MP} }}{{\overline {OP} }} = \sin \theta [/tex]
[tex]\left( {{{90}^ \circ } - \theta } \right) = \frac{{\overline {NQ} }}{{\overline {ON} }} = \frac{{\overline {OM} }}{{\overline {MP} }} = \cot \theta [/tex]
অতএব
[tex]cosec\left( {{{90}^ \circ } - \theta } \right) = \frac{1}{{\sin \left( {{{90}^ \circ } - \theta } \right)}} = \frac{1}{{\cos \theta }} = \sec \theta [/tex]
একইভাবে
[tex]sec\left( {{{90}^ \circ } - \theta } \right) = \frac{1}{{\cos \left( {{{90}^ \circ } - \theta } \right)}} = \frac{1}{{\sin \theta }} = \cos ec\theta [/tex]
এবং [tex]\cot \left( {{{90}^ \circ } - \theta } \right) = \tan \theta [/tex]
(৩) [tex]\left( {{{90}^ \circ } + \theta } \right)[/tex] কোণের কোণানুপাত (Trigonometrical ratios of) [tex]\left( {{{90}^ \circ } + \theta } \right)[/tex]
মনে করি ঘূর্ণিয়মান OA সরলরেখা O বিন্দুকে কেন্দ্র করে ঘড়ির কাটার বিপরীতদিকে আবর্তন করে এবং প্রাথমিক অবস্থান OX থেকে OA অবস্থানে এসে [tex]\angle XOA = \theta [/tex] উৎপন্ন করে। তারপর রেখাটি একইদিকে ঘুরে [tex]\angle AOB = {90^ \circ }[/tex] উৎপন্ন করলে [tex]\angle XOB = {90^ \circ } + \theta [/tex] হবে ।
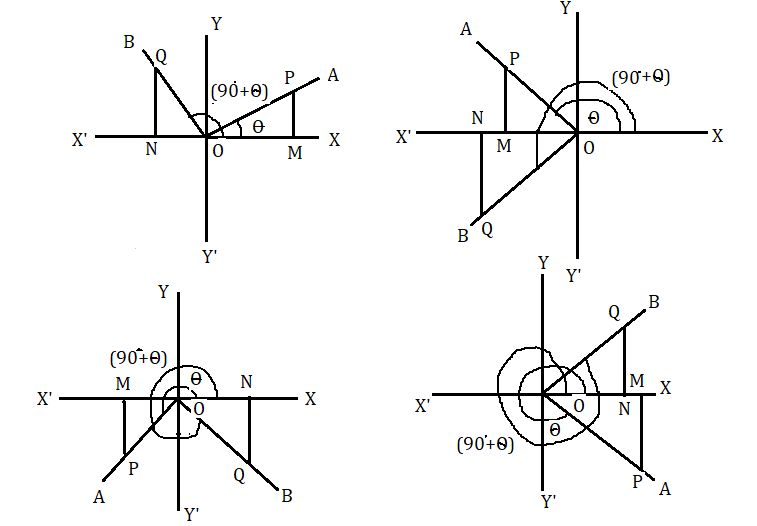
[tex]\overline {OA} [/tex] সরলরেখার উপরে যেকোনো বিন্দু P নেওয়া হল। P বিন্দু থেকে [tex]\overline {OX} [/tex] এর উপর [tex]\overline {PM} [/tex] লম্ব টানা হল। আবার [tex]\overline {OB} [/tex] সরলরেখার উপরে Q এমন একটি বিন্দু নেওয়া হল যাতে [tex]\overline {OP} = \overline {OQ} [/tex] হয়।
এখন OPM ও OQN সমকোণী ত্রিভুজ দুটিতে [tex]\angle POM = \angle OQN[/tex]
যেহেতু [tex]\overline {OB} \bot \overline {OA} [/tex] , [tex]\overline {OP} = \overline {OQ} [/tex] এবং [tex]\angle POM = \angle OQN[/tex]
সুতরাং ত্রিভুজ দুটি সর্বসম
অতএব [tex]\overline {MP} = - \overline {ON} [/tex] , [tex]\overline {NQ} = \overline {OM} [/tex] এবং [tex]\overline {OQ} = \overline {OP} [/tex]
সুতরাং সংজ্ঞানুযায়ী
[tex]\sin \left( {{{90}^ \circ } + \theta } \right) = \frac{{\overline {NQ} }}{{\overline {OQ} }} = \frac{{\overline {OM} }}{{\overline {OP} }} = \cos \theta [/tex]
[tex]\cos \left( {{{90}^ \circ } + \theta } \right) = \frac{{\overline {ON} }}{{\overline {OQ} }} = \frac{{ - \overline {MP} }}{{\overline {OP} }} = - sin\theta [/tex]
[tex]\tan \left( {{{90}^ \circ } + \theta } \right) = \frac{{\overline {NQ} }}{{\overline {ON} }} = \frac{{\overline {OM} }}{{\overline { - MP} }} = - \cot \theta [/tex]
[tex]\cos ec\left( {{{90}^ \circ } + \theta } \right) = \frac{1}{{\sin \left( {{{90}^ \circ } + \theta } \right)}} = \frac{1}{{\cos \theta }} = \sec \theta [/tex]
[tex]\sec \left( {{{90}^ \circ } + \theta } \right) = \frac{1}{{\cos \left( {{{90}^ \circ } + \theta } \right)}} = \frac{1}{{ - \sin \theta }} = - \cos ec\theta [/tex]
[tex]\cot \left( {{{90}^ \circ } + \theta } \right) = \frac{1}{{\tan \left( {{{90}^ \circ } + \theta } \right)}} = \frac{1}{{ - \cot \theta }} = - \tan \theta [/tex]
(৪) [tex]\left( {{{180}^ \circ } - \theta } \right)[/tex] কোণের কোণানুপাত ( Trigonometrical ratios of [tex]\left( {{{180}^ \circ } - \theta } \right)[/tex])
(২) ও (৩) এর সাহায্যেই খুব সহজেই [tex]\left( {{{180}^ \circ } - \theta } \right)[/tex] কোণের কোণানুপাতসমূহ নির্ণয় করা যায়।
[tex]\begin{array}{l}
\sin \left( {{{180}^ \circ } - \theta } \right)\\
= \sin \left[ {{{90}^ \circ } + \left( {{{90}^ \circ } - \theta } \right)} \right]\\
= \cos \left( {{{90}^ \circ } - \theta } \right)\\
= \sin \theta
\end{array}[/tex]
[tex]\begin{array}{l}
\cos \left( {{{180}^ \circ } - \theta } \right)\\
= \cos \left[ {{{90}^ \circ } + \left( {{{90}^ \circ } - \theta } \right)} \right]\\
= - \sin \left( {{{90}^ \circ } - \theta } \right)\\
= - \cos \theta
\end{array}[/tex]
[tex]\begin{array}{l}
\tan \left( {{{180}^ \circ } - \theta } \right)\\
= \tan \left[ {{{90}^ \circ } + \left( {{{90}^ \circ } - \theta } \right)} \right]\\
= - \cot \left( {{{90}^ \circ } - \theta } \right)\\
= - \tan \theta
\end{array}[/tex]
[tex]\begin{array}{l}
\cos ec\left( {{{180}^ \circ } - \theta } \right)\\
= \frac{1}{{\sin \left( {{{180}^ \circ } - \theta } \right)}}\\
= \frac{1}{{\sin \theta }}\\
= \cos ec\theta
\end{array}[/tex]
[tex]\begin{array}{l}
\sec \left( {{{180}^ \circ } - \theta } \right)\\
= \frac{1}{{\cos \left( {{{180}^ \circ } - \theta } \right)}}\\
= \frac{1}{{ - \cos \theta }}\\
= - \sec \theta
\end{array}[/tex]
[tex]\begin{array}{l}
\cot \left( {{{180}^ \circ } - \theta } \right)\\
= \frac{1}{{\tan \left( {{{180}^ \circ } - \theta } \right)}}\\
= \frac{1}{{ - \tan \theta }}\\
= - \cot \theta
\end{array}[/tex]
(৫) [tex]\left( {{{180}^ \circ } + \theta } \right)[/tex] কোণের কোণানুপাত ( Trigonometrical ratios of [tex]\left( {{{180}^ \circ } + \theta } \right)[/tex] )
আমরা এর আগের প্রমাণের সাহায্যে খুব সহজেই [tex]\left( {{{180}^ \circ } + \theta } \right)[/tex] কোণের কোণানুপাত নির্ণয় করতে পারি।
[tex]\begin{array}{l}
\sin \left( {{{180}^ \circ } + \theta } \right)\\
= \sin \left[ {{{90}^ \circ } + \left( {{{90}^ \circ } + \theta } \right)} \right]\\
= \cos \left( {{{90}^ \circ } + \theta } \right)\\
= - \sin \theta
\end{array}[/tex]
[tex]\begin{array}{l}
\cos \left( {{{180}^ \circ } + \theta } \right)\\
= \cos \left[ {{{90}^ \circ } + \left( {{{90}^ \circ } + \theta } \right)} \right]\\
= - \sin \left( {{{90}^ \circ } + \theta } \right)\\
= - \cos \theta
\end{array}[/tex]
[tex]\begin{array}{l}
\tan \left( {{{180}^ \circ } + \theta } \right)\\
= \tan \left[ {{{90}^ \circ } + \left( {{{90}^ \circ } + \theta } \right)} \right]\\
= - \cot \left( {{{90}^ \circ } + \theta } \right)\\
= - \left( { - \tan \theta } \right)\\
= \tan \theta
\end{array}[/tex]
[tex]\begin{array}{l}
\cos ec\left( {{{180}^ \circ } + \theta } \right)\\
= \frac{1}{{\sin \left( {{{180}^ \circ } + \theta } \right)}}\\
= \frac{1}{{ - \sin \left( {{{180}^ \circ } + \theta } \right)}}\\
= - \cos ec\theta
\end{array}[/tex]
[tex]\begin{array}{l}
\sec \left( {{{180}^ \circ } + \theta } \right)\\
= \frac{1}{{\cos \left( {{{180}^ \circ } + \theta } \right)}}\\
= \frac{1}{{ - \cos \theta }}\\
= - \sec \theta
\end{array}[/tex]
[tex]\begin{array}{l}
\cot \left( {{{180}^ \circ } + \theta } \right)\\
= \frac{1}{{\tan \left( {{{180}^ \circ } + \theta } \right)}}\\
= \frac{1}{{\tan \theta }}\\
= \cot \theta
\end{array}[/tex]
(৬) [tex]\left( {{{270}^ \circ } - \theta } \right)[/tex] এবং [tex]\left( {{{270}^ \circ } + \theta } \right)[/tex] এর কোণের কোণানুপাত ( Trigonometrical ratios of [tex]\left( {{{270}^ \circ } - \theta } \right)[/tex] and [tex]\left( {{{270}^ \circ } + \theta } \right)[/tex] )
উপরের কোণানুপাতের মান গুলি প্রয়োগ করে আমরা সহজেই [tex]\left( {{{270}^ \circ } - \theta } \right)[/tex] এবং [tex]\left( {{{270}^ \circ } + \theta } \right)[/tex] কোণের কোণানুপাতসমূহের মান নির্ণয় করতে পারি
[tex]\begin{array}{l}
\sin \left( {{{270}^ \circ } - \theta } \right)\\
= \sin \left[ {{{180}^ \circ } + \left( {{{90}^ \circ } - \theta } \right)} \right]\\
= - \sin \left( {{{90}^ \circ } - \theta } \right)\\
= - \cos \theta
\end{array}[/tex]
[tex]\begin{array}{l}
\sin \left( {{{270}^ \circ } + \theta } \right)\\
= \sin \left[ {{{180}^ \circ } + \left( {{{90}^ \circ } + \theta } \right)} \right]\\
= - \sin \left( {{{90}^ \circ } + \theta } \right)\\
= - \cos \theta
\end{array}[/tex]
[tex]\begin{array}{l}
\cos \left( {{{270}^ \circ } - \theta } \right)\\
= \cos \left[ {{{180}^ \circ } + \left( {{{90}^ \circ } - \theta } \right)} \right]\\
= - \cos \left( {{{90}^ \circ } - \theta } \right)\\
= - \sin \theta
\end{array}[/tex]
[tex]\begin{array}{l}
\cos \left( {{{270}^ \circ } + \theta } \right)\\
= \cos \left[ {{{180}^ \circ } + \left( {{{90}^ \circ } + \theta } \right)} \right]\\
= - \cos \left( {{{90}^ \circ } + \theta } \right)\\
= - \left( { - \sin \theta } \right)\\
= \sin \theta
\end{array}[/tex]
[tex]\begin{array}{l}
\tan \left( {{{270}^ \circ } - \theta } \right)\\
= \tan \left[ {{{180}^ \circ } + \left( {{{90}^ \circ } - \theta } \right)} \right]\\
= \tan \left( {{{90}^ \circ } - \theta } \right)\\
= \cot \theta
\end{array}[/tex]
[tex]\begin{array}{l}
\tan \left( {{{270}^ \circ } + \theta } \right)\\
= \tan \left[ {{{180}^ \circ } + \left( {{{90}^ \circ } + \theta } \right)} \right]\\
= \tan \left( {{{90}^ \circ } + \theta } \right)\\
= - \cot \theta
\end{array}[/tex]
একইভাবে অন্যান্য কোণানুপাতের মান নির্ণয় করা যায়।
(৭) [tex]\left( {{{360}^ \circ } \pm \theta } \right)[/tex] এবং [tex]\left( {n \cdot {{360}^ \circ } \pm \theta } \right)[/tex] কোণসমূহের কোণানুপাত ( Trigonometrical ratios of [tex]\left( {{{360}^ \circ } \pm \theta } \right)[/tex] and [tex]\left( {n \cdot {{360}^ \circ } \pm \theta } \right)[/tex] )
n এর মান ধনাত্মক বা ঋণাত্মক অখন্ড সংখ্যা হলে [tex]\left( {n \cdot {{360}^ \circ } \pm \theta } \right)[/tex] কোণের কোণানুপাত [tex]\left( { \pm \theta } \right)[/tex] কোণের কোণানুপাতের সমান হয়। সুতরাং
[tex]\begin{array}{l}
\sin \left( {n \cdot {{360}^ \circ } + \theta } \right) = \sin \theta \\
\sin \left( {n \cdot {{360}^ \circ } - \theta } \right) = \sin \left( { - \theta } \right) = - \sin \theta \\
\cos \left( {n \cdot {{360}^ \circ } + \theta } \right) = \cos \theta \\
\cos \left( {n \cdot {{360}^ \circ } - \theta } \right) = \cos \left( { - \theta } \right) = \cos \theta \\
\tan \left( {n \cdot {{360}^ \circ } + \theta } \right) = \tan \theta \\
\tan \left( {n \cdot {{360}^ \circ } - \theta } \right) = \tan \left( { - \theta } \right) = - \tan \theta
\end{array}[/tex]
সংক্ষিপ্তকরণ ( Summarisation )
নির্দিষ্ট কোণ [tex]\theta [/tex] এর সাথে সংযুক্ত কোনো কোণ [tex]\left( {n \cdot {{90}^ \circ } \pm \theta } \right)\[/tex]এর কোণানুপাত নির্ণয় করতে হলে নিম্নলিখিত পদ্ধতিতে অগ্রসর হতে হয়
(a) প্রথমত [tex]\theta [/tex] সূক্ষকোণ ধরে [tex]\left( {n \cdot {{90}^ \circ } \pm \theta } \right)\[/tex] এর মান কোনো পদে অবস্থিত তা নির্ণয় করতে হবে। " all , sin , tan , cos " সূত্রের সাহায্যে কোণানুপাতের চিহ্ন কি হবে তা স্থির করতে হবে। অর্থাৎ
- [tex]\left( {n \cdot {{90}^ \circ } \pm \theta } \right)[/tex] এর মান প্রথম পাদে থাকলে সব কোণানুপাত ধনাত্মক
- [tex]\left( {n \cdot {{90}^ \circ } \pm \theta } \right)[/tex] এর মান দ্বিতীয় পাদে থাকলে কেবল sin এবং cosec ধনাত্মক
- [tex]\left( {n \cdot {{90}^ \circ } \pm \theta } \right)[/tex] এর মান তৃতীয় পাদে থাকলে tan এবং cot ধনাত্মক
- [tex]\left( {n \cdot {{90}^ \circ } \pm \theta } \right)[/tex] এর মান চতুর্থ পাদে থাকলে কেবল cos এবং sec ধনাত্মক
(b) চিহ্ন নির্ধারণ করার পর দেখতে হবে n এর মান যুগ্ম অথবা অযুগ্ম কি না। যদি n এর মান যুগ্ম অখন্ড সংখ্যা হয় তবে কোণানুপাতের আকার অপরিবর্তিত থাকবে অর্থাৎ [tex]\sin \left( {n \cdot {{90}^ \circ } \pm \theta } \right)[/tex] = [tex]\sin \theta [/tex] অথবা [tex]\sin \left( { - \theta } \right)[/tex] ; [tex]\cos \left( {n \cdot {{90}^ \circ } \pm \theta } \right)[/tex] = [tex]\cos \theta [/tex] অথবা [tex]\cos \left( { - \theta } \right)[/tex] ; [tex]\tan \left( {n \cdot {{90}^ \circ } \pm \theta } \right)[/tex] = [tex]\tan \theta [/tex] অথবা [tex]\tan \left( { - \theta } \right)[/tex] ইত্যাদি হবে। কিন্তু n এর মান অযুগ্ম অখন্ড সংখ্যা হলে কোণানুপাতের আকার পরিবর্তিত হবে অর্থাৎ [tex]\sin \left( {n \cdot {{90}^ \circ } \pm \theta } \right)[/tex] = [tex]\cos \theta [/tex] অথবা [tex]\cos \left( { - \theta } \right)[/tex] ; [tex]\cos \left( {n \cdot {{90}^ \circ } \pm \theta } \right)[/tex] = [tex]\sin \theta [/tex] অথবা [tex]sin\left( { - \theta } \right)[/tex] ; [tex]\tan \left( {n \cdot {{90}^ \circ } \pm \theta } \right)[/tex] = [tex]\cot \theta [/tex] অথবা [tex]\cot \left( { - \theta } \right)[/tex] ইত্যাদি হবে।
- 1282 views