যৌগিক কোণের কোণানুপাত ( Trigonometrical Ratios of Compound Angles )

 যৌগিক কোণের কোণানুপাত  ( Trigonometrical Ratios of Compound Angles )

সূচনা ( Introduction )

দুই বা ততোধিক কোণের বীজগাণিতিক সমষ্টিকে যৌগিক বা মিশ্র ( Compound angle ) কোণ বলে। উদাহরণস্বরূপ A , B ও  C তিনটি কোণ হলে ( A+B ) , ( A+C ) , ( B+C ) , ( A-B+C ) ইত্যাদি হল যৌগিক কোণ। এই অধ্যায়ে আমরা যৌগিক কোণের ত্রিকোণমিতিক কোণানুপাত সম্পর্কে আলোচনা করব। 

উপপাদ্য ( Theorem )

উপপাদ্য ১ : A , B এবং ( A+B ) ধনাত্মক সূক্ষকোণ হলে , প্রমাণ করতে হবে যে 

1. $\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B$
2. $\cos \left( {A + B} \right) = \cos A\cos B - \sin A\sin B$

মনে করি ঘূর্ণিয়মান $\overrightarrow {OX}$ সরলরেখা O বিন্দুকে কেন্দ্র করে ঘড়ির কাঁটার বিপরীত দিকে আবর্তন করে এবং প্রাথমিক অবস্থান $\overrightarrow {OX}$ থেকে $\overrightarrow {OY}$ অবস্থানে এসে $\angle XOY = A$ সূক্ষকোণ উৎপন্ন করে। 

তারপর রেখাটি একই দিকে আবর্তন করে  $\overrightarrow {OY}$ অবস্থান থেকে $\overrightarrow {OZ}$ অবস্থানে আসে এবং $\angle YOZ = B$ সূক্ষকোণ উৎপন্ন করে। তাহলে যদি $\angle XOZ = A + B < {90^ \circ }$ হয়। 

প্রমাণ করতে হবে 

1. $\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B$
2. $\cos \left( {A + B} \right) = \cos A\cos B - \sin A\sin B$

অঙ্কন : ( A+B ) যৌগিক কোণের অন্তিম বাহু  $\overrightarrow {OZ}$ ওপর যেকোনো বিন্দু P নেওয়া হল এবং P বিন্দু থেকে 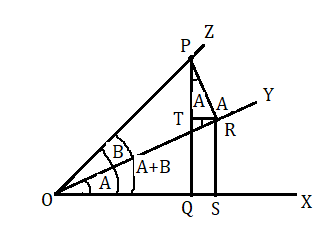 $\overrightarrow {OX}$ এবং $\overrightarrow {OY}$ সরলরেখার উপরে $\overrightarrow {PQ}$ এবং $\overrightarrow {PR}$ লম্ব টানা হল। তারপর R বিন্দু থেকে  $\overrightarrow {OX}$ এবং $\overrightarrow {PQ}$ এর ওপর যথাক্রমে $\overrightarrow {RS}$ এবং $\overrightarrow {RT}$ লম্ব টানা হল। 

প্রমাণ : স্পষ্টতই $\angle TPR + \angle PRT = {90^ \circ }$

এবং $\angle ORT + \angle PRT = {90^ \circ }$

সুতরাং $\angle TPR = \angle ORT =$ একান্তর $\angle ROX = A$

এখন সমকোণী ত্রিভুজের POQ থেকে পাই 

$\begin{array}{l} \sin \left( {A + B} \right)\\  = \frac{{\overrightarrow {PQ} }}{{\overrightarrow {OP} }} = \frac{{\overrightarrow {PT}  + \overrightarrow {TQ} }}{{\overrightarrow {OP} }} = \frac{{\overrightarrow {PT} }}{{\overrightarrow {OP} }} + \frac{{\overrightarrow {TQ} }}{{\overrightarrow {OP} }} = \frac{{\overrightarrow {PT} }}{{\overrightarrow {OP} }} + \frac{{\overrightarrow {RS} }}{{\overrightarrow {OP} }}\\  = \frac{{\overrightarrow {PT} }}{{\overrightarrow {PR} }} \cdot \frac{{\overrightarrow {PR} }}{{\overrightarrow {OP} }} + \frac{{\overrightarrow {RS} }}{{\overrightarrow {OR} }} \cdot \frac{{\overrightarrow {OR} }}{{\overrightarrow {OP} }}\\  = \cos A\sin B + \sin A\cos B\\  = \sin A\cos B + \cos A\sin B \end{array}$