ধনাত্মক সূক্ষ্মকোণের ত্রিকোনমিতিক কোনানুপাত ও আদর্শ কোণসমূহ (Trigonometrical Ratios of Positive Acute Angles and Standard Angles)

ধনাত্মক সূক্ষ্মকোণের ত্রিকোনমিতিক কোনানুপাত ও আদর্শ কোণসমূহ (Trigonometrical Ratios of Positive Acute Angles and Standard Angles)

সূচনা ( Introduction )

ত্রিভুজের তিনটি কোণ ও তিনটি বাহুর পরিমাপ এবং তাদের পারস্পরিক সম্বন্ধ সম্পর্কে আলোচনাই ত্রিকোণমিতির বিষয়বস্তু। এজন্য ত্রিকোণমিতিক কোণানুপাত সম্পর্কে আমাদের জানতে হবে। এই অধ্যায়ে ধনাত্মক ত্রিকোণমিতিক কোণানুপাত এবং তাদের পারস্পরিক সম্পর্ক সম্মন্ধে আলোচনা করা হয়েছে। 

ত্রিকোণমিতিক কোণানুপাতসমূহ (Trigonometrical Ratios of Angles)

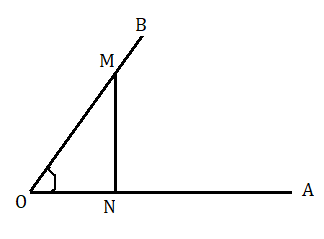মনে করি OA একটি ঘূর্ণিয়মান সরলরেখা । এটি এর প্রাথিমিক অবস্থান OA থেকে ঘড়ির কাটার বিপরীত দিকে ঘুরে OB অবস্থানে গেল এবং [tex]\angle AOB[/tex] কোণ উৎপন্ন করল। মনে করি [tex]\angle AOB = \theta [/tex] . এটি একটি সূক্ষকোণ OB বাহুর উপরে M যেকোনো একটি বিন্দু নেওয়া হল এবং M থেকে OA বাহুর উপরে MN লম্ব টানা হল। স্পষ্টতইMON একটি সমকোণী ত্রিভুজ হবে। যার [tex]\theta [/tex] কোণের সাপেক্ষে OM হল অতিভুজ এবং ON হল ভূমি । 

এখন [tex]\theta [/tex] কোণের কোণানুপাতের সংজ্ঞা থেকে পাই 

[tex]\frac{{MN}}{{OM}}[/tex] অনুপাতকে [tex]\theta [/tex] কোণের sine বা সংক্ষেপে [tex]\sin \theta [/tex] ,

[tex]\frac{{ON}}{{OM}}[/tex] অনুপাতকে [tex]\theta [/tex] কোণের cosine বা সংক্ষেপে [tex]\cos \theta [/tex] ,

[tex]\frac{{MN}}{{ON}}[/tex] অনুপাতকে [tex]\theta [/tex] কোণের tangent  বা সংক্ষেপে [tex]\tan \theta [/tex] ,

[tex]\frac{{OM}}{{MN}}[/tex] অনুপাতকে [tex]\theta [/tex] কোণের cosecant  বা সংক্ষেপে [tex]\cos ec\theta [/tex] ,

[tex]\frac{{OM}}{{ON}}[/tex] অনুপাতকে [tex]\theta [/tex] কোণের secant বা সংক্ষেপে [tex]\sec\theta [/tex] 

এবং [tex]\frac{{ON}}{{MN}}[/tex] অনুপাতকে [tex]\theta [/tex] কোণের cotangent বা সংক্ষেপে [tex]\cot \theta [/tex] বলা হয়। 

[tex]\theta [/tex] কোণের সাপেক্ষে উপরের উল্লেখিত অনুপাতকে ত্রিকোণমিতিক কোণানুপাত বলা হয় । 

একটি প্রদত্ত কোণের ত্রিকোণমিতিক অনুপাত অভিন্ন (The Trigonometrical Ratios are always the same for a given angle) 

একটি প্রদত্ত কোণের ত্রিকোণমিতিক কোণানুপাতগুলি সমকোণী ত্রিভুজের দুটি বাহুর অনুপাত দ্বারা প্রকাশ করা হয় । যদি কোণের মান অপরিবর্তিত থাকে কিন্তু ত্রিভুজের আকার পরিবর্তিত হয় তবে কোণানুপাতগুলির মানের কোনো পরিবর্তন হবেনা । 

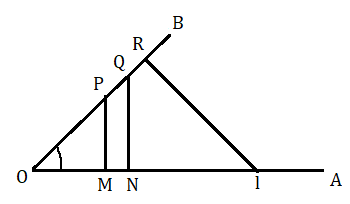মনে করি [tex]\angle AOB = \theta [/tex] ; OB বাহুর উপরে যেকোনো দুটি বিন্দু P ও Q নেওয়া হল এবং বিন্দু দুটি থেকে OA বাহুর উপরে যথাক্রমে PM এবং QN লম্ব টানা হল। আবার OA বাহুর উপরে L যেকোনো বিন্দু নেওয়া হল এবং L  বিন্দু থেকে OB বাহুর উপরে LR লম্ব টানা হল। 

কোণানুপাতের সংজ্ঞা থেকে আমরা লিখতে পারি 

POM ত্রিভুজের [tex]\sin \theta  = \frac{{PM}}{{OP}}[/tex]

QON ত্রিভুজের [tex]\sin \theta  = \frac{{QN}}{{OQ}}[/tex]

এবং LOR ত্রিভুজের [tex]\sin \theta  = \frac{{LR}}{{OL}}[/tex]

এখানে দেখা যাচ্ছে ত্রিভুজ POM , ত্রিভুজ QON এবং ত্রিভুজ LOR এর সাধারণ কোণ [tex]\theta [/tex]

এবং [tex]\angle PMO = \angle QNO = \angle LRO = {90^ \circ }[/tex] 

সুতরাং অবশিষ্ট কোণগুলি পরস্পরের সঙ্গে সমান হবে 

অতএব [tex]\angle MOP = \angle NQO = \angle OLR[/tex]

অতএব ত্রিভুজ POM , ত্রিভুজ QON এবং ত্রিভুজ LOR সদৃশকোণী 

সুতরাং [tex]\frac{{PM}}{{OP}} = \frac{{QN}}{{OQ}} = \frac{{LR}}{{OL}}[/tex]

উপরের আলোচনা থেকে সহজেই বোঝা যাচ্ছে যে ত্রিভুজের আকারের পরিবর্তন হলেও ত্রিভুজের [tex]\sin \theta [/tex] মানের কোনো পরিবর্তন হয়না। [tex]\sin \theta [/tex] এর মান কেবল কোণের মানের উপর নির্ভর করে। 

একইভাবে প্রমাণ করা যায় অন্যান্য কোণানুপাতের মান কেবল কোণের মানের উপর নির্ভর করে। ত্রিভুজের আকারের উপর নয় । 

ত্রিকোণমিতিক কোণানুপাতের পারস্পরিক সম্মন্ধ (Relations among the Trigonometrical Ratios)

এই চিত্র থেকে পাই

[tex]\sin \theta  = \frac{{MN}}{{OM}}[/tex].............(i)

এবং [tex]\cos ec\theta  = \frac{{OM}}{{MN}}[/tex].............(ii)

(i) ও (ii) গুণ করে পাই 

[tex]\begin{array}{l}
\sin \theta  \cdot \cos ec\theta  = \frac{{MN}}{{OM}} \cdot \frac{{OM}}{{MN}} = 1\\
 \Rightarrow \sin \theta  \cdot \cos ec\theta  = 1\\
 \Rightarrow \sin \theta  = \frac{1}{{\cos ec\theta }}\\
or,\cos ec\theta  = \frac{1}{{\sin \theta }}
\end{array}[/tex]

একইভাবে চিত্র থেকে পাই 

[tex]\cos \theta  = \frac{{ON}}{{OM}}[/tex]..............(iii)

এবং [tex]\sec \theta  = \frac{{OM}}{{ON}}[/tex]..............(iv)

(iii) ও (iv) গুণ করে পাই

[tex]\begin{array}{l}
\cos \theta  \cdot \sec \theta  = \frac{{ON}}{{OM}} \cdot \frac{{OM}}{{ON}} = 1\\
 \Rightarrow \cos \theta  \cdot \sec \theta  = 1\\
 \Rightarrow \cos \theta  = \frac{1}{{\sec \theta }}\\
or,\sec \theta  = \frac{1}{{\cos \theta }}
\end{array}[/tex]

আবার চিত্র থেকে পাই 

[tex]\tan \theta  = \frac{{MN}}{{ON}}[/tex].............(v)

এবং [tex]\cot \theta  = \frac{{ON}}{{MN}}[/tex]...............(vi)

(v) ও (vi) গুণ করে পাই

[tex]\begin{array}{l}
\tan \theta  \cdot \cot \theta  = \frac{{MN}}{{ON}} \cdot \frac{{ON}}{{MN}} = 1\\
 \Rightarrow \tan \theta  \cdot \cot \theta  = 1\\
 \Rightarrow \tan \theta  = \frac{1}{{\cot \theta }}\\
or,\cot \theta  = \frac{1}{{\tan \theta }}
\end{array}[/tex]

আবার 

[tex]\tan \theta  = \frac{{MN}}{{ON}} = \frac{{\frac{{MN}}{{OM}}}}{{\frac{{ON}}{{OM}}}} = \frac{{\sin \theta }}{{\cos \theta }}[/tex]

এবং [tex]\cot \theta  = \frac{{ON}}{{MN}} = \frac{{\frac{{ON}}{{OM}}}}{{\frac{{MN}}{{OM}}}} = \frac{{\cos \theta }}{{\sin \theta }}[/tex]

আবার OMN সমকোণী ত্রিভুজের [tex]\angle ONM = {90^ \circ }[/tex] = 1 সমকোণ 

অতএব পিথাগোরাসের উপপাদ্য অনুযায়ী 

[tex]M{N^2} + O{N^2} = O{M^2}[/tex] ................(vii)

উপরের সমীকরণের উভয়পক্ষকে [tex]O{M^2}[/tex] দিয়ে ভাগ করে পাই 

[tex]\begin{array}{l}
\frac{{M{N^2}}}{{O{M^2}}} + \frac{{O{N^2}}}{{O{M^2}}} = 1\\
 \Rightarrow {\left( {\frac{{MN}}{{OM}}} \right)^2} + {\left( {\frac{{ON}}{{OM}}} \right)^2} = 1\\
 \Rightarrow {\sin ^2}\theta  + {\cos ^2}\theta  = 1
\end{array}[/tex]

আবার (vii) নং সমীকরণকে [tex]O{N^2}[/tex] দিয়ে ভাগ করে পাই 

[tex]\begin{array}{l}
\frac{{M{N^2}}}{{O{N^2}}} + 1 = \frac{{O{M^2}}}{{O{N^2}}}\\
 \Rightarrow {\left( {\frac{{OM}}{{ON}}} \right)^2} - {\left( {\frac{{MN}}{{ON}}} \right)^2} = 1\\
 \Rightarrow {\sec ^2}\theta  - {\tan ^2}\theta  = 1
\end{array}[/tex]

 সবশেষে (vii) নং সমীকরণকে আবার [tex]M{N^2}[/tex] দিয়ে ভাগ করে পাই 

[tex]\begin{array}{l}
\frac{{M{N^2}}}{{M{N^2}}} + \frac{{O{N^2}}}{{M{N^2}}} = \frac{{O{M^2}}}{{M{N^2}}}\\
 \Rightarrow 1 + {\left( {\frac{{ON}}{{MN}}} \right)^2} = {\left( {\frac{{OM}}{{MN}}} \right)^2}\\
 \Rightarrow \left( {\frac{{OM}}{{MN}}} \right) - \left( {\frac{{ON}}{{MN}}} \right) = 1\\
 \Rightarrow \cos e{c^2}\theta  - {\cot ^2}\theta  = 1
\end{array}[/tex]

ত্রিকোণমিতিক কোণানুপাতসমূহের মানের সীমা ( Limits of the values of Trigonometrical Ratios )

পাশের চিত্র থেকে আমরা পরিষ্কার একটি ধারণা করতে পারি যে 

[tex]\sin \theta  = \frac{{MN}}{{OM}}[/tex]

এবং [tex]\cos \theta  = \frac{{ON}}{{OM}}[/tex]

এখন OM হল সমকোণী ত্রিভুজ OMN এর অতিভুজ। সুতরাং OM এর মান কখনো MN এবং ON এর থেকে ছোটো হতে পারেনা। সুতরাং আমরা বলতে পারি যে [tex]\frac{{MN}}{{OM}}[/tex] এবং [tex]\frac{{ON}}{{OM}}[/tex] কখনো 1 এর থেকে বড়ো হবে না। অতএব [tex]\sin \theta [/tex] এবং [tex]\cos \theta [/tex] এর মান  কখনো 1 এর থেকে বড়ো হবে না । 

আবার [tex]\cos ec\theta  = \frac{{OM}}{{MN}}[/tex] এবং [tex]\sec \theta  = \frac{{OM}}{{ON}}[/tex] . এর থেকে বোঝা যাচ্ছে [tex]\cos ec\theta [/tex] এবং [tex]sec\theta [/tex] এর মান কখনো 1 এর থেকে ছোটো হবে না । 

সবশেষে [tex]\tan \theta  = \frac{{MN}}{{ON}}[/tex] এবং [tex]\cot \theta  = \frac{{ON}}{{MN}}[/tex] .

স্পষ্টতই MN এর মান ON এর থেকে বড়ো বা ছোটো দুটোই হতে পারে। সুতরাং [tex]\tan \theta [/tex] এবং [tex]\cot \theta [/tex] এর মান যেকোনো ধনাত্মক মান হতে পারে । 

সুতরাং [tex]\theta [/tex] ধনাত্মক সূক্ষকোণ হলে কোণানুপাতগুলি ঋণাত্মক হবে না এবং  

1. [tex]\sin \theta [/tex] এবং [tex]\cos \theta [/tex] এর মান  কখনো 1 এর থেকে বড়ো হবে না । 
2. [tex]\cos ec\theta [/tex] এবং [tex]sec\theta [/tex] এর মান কখনো 1 এর থেকে ছোটো হবে না । 
3. [tex]\tan \theta [/tex] এবং [tex]\cot \theta [/tex] এর মান যেকোনো ধনাত্মক মান হতে পারে । 

আদর্শ কোণ সমূহের কোণানুপাত (Trigonometrical Ratios of Standard Angles)

ত্রিকোণমিতিতে [tex]{0^ \circ }[/tex] , [tex]{30^ \circ }[/tex] , [tex]{45^ \circ }[/tex] , [tex]{60^ \circ }[/tex] ও [tex]{90^ \circ }[/tex] কোণগুলিকে আদর্শ কোণ বলা হয় এবং তাদের কোণানুপাত সমূহ বহুল ব্যব্যহৃত হয়। সেইজন্যে এই কোণ গুলির কোণানুপাত সমূহের মান মনে রাখা প্রয়োজন। নীচে আদর্শ কোণগুলির sine , cosine ও tangent এর মানসমূহ তালিকা বদ্ধ করে দেখানো হয়েছে। 

কোণ	[tex]{0^ \circ }[/tex]	[tex]{30^ \circ }[/tex]	[tex]{45^ \circ }[/tex]	[tex]{60^ \circ }[/tex]	[tex]{90^ \circ }[/tex]
sin	0	[tex]\frac{1}{2}[/tex]	[tex]\frac{1}{{\sqrt 2 }}[/tex]	[tex]\frac{{\sqrt 3 }}{2}[/tex]	1
cos	1	[tex]\frac{{\sqrt 3 }}{2}[/tex]	[tex]\frac{1}{{\sqrt 2 }}[/tex]	[tex]\frac{1}{2}[/tex]	0
tan	0	[tex]\frac{1}{{\sqrt 3 }}[/tex]	1	[tex]{\sqrt 3 }[/tex]	অসংজ্ঞাত

 

সংক্ষিপ্তকরণ (Summarisation)

1. [tex]\sin \theta \cos ec\theta  = 1 \Rightarrow \cos ec\theta  = \frac{1}{{\sin \theta }}[/tex]
2. [tex]\cos \theta \sec \theta  = 1 \Rightarrow \sec \theta  = \frac{1}{{\cos \theta }}[/tex]
3. [tex]\tan \theta \cot \theta  = 1 \Rightarrow \cot \theta  = \frac{1}{{\tan \theta }}[/tex]
4. [tex]\tan \theta  = \frac{{\sin \theta }}{{\cos \theta }}[/tex]
5. [tex]\cot \theta  = \frac{{\cos \theta }}{{\sin \theta }}[/tex]
6. [tex]{\sin ^2}\theta [/tex] বলতে যেমন [tex]{\left( {\sin \theta } \right)^2}[/tex] তেমন [tex]{\tan ^3}\theta [/tex] বলতে বোঝায় [tex]{\left( {\tan \theta } \right)^3}[/tex]
7. [tex]{\sin ^2}\theta  + {\cos ^2}\theta  = 1[/tex]
8. [tex]{\sec ^2}\theta  = 1 + {\tan ^2}\theta [/tex]
9. [tex]co{\sec ^2}\theta  = 1 + {\cot ^2}\theta [/tex]
10. [tex]\sin \theta [/tex] এবং [tex]\cos \theta [/tex] এর মান  কখনো 1 এর থেকে বড়ো হবে না। 
11. [tex]\cos ec\theta [/tex] এবং [tex]sec\theta [/tex] এর মান কখনো 1 এর থেকে ছোটো হবে না। 
12. [tex]\tan \theta [/tex] এবং [tex]\cot \theta [/tex] এর মান যেকোনো ধনাত্মক মান হতে পারে।