
নবম অধ্যায়ঃ ত্রিকোনমিতিক বিপরীত বৃত্তীয় অপেক্ষকসমূহ
নবম অধ্যায়ঃ ত্রিকোনমিতিক বিপরীত বৃত্তীয় অপেক্ষকসমূহ

দশম অধ্যায়ঃ ত্রিভুজের ধর্মাবলী
দশম অধ্যায়ঃ ত্রিভুজের ধর্মাবলী

নবম অধ্যায়ঃত্রিকোনমিতিক বিপরীত বৃত্তীয় অপেক্ষকসমূহ
নবম অধ্যায়ঃত্রিকোনমিতিক বিপরীত বৃত্তীয় অপেক্ষকসমূহ

অষ্টম অধ্যায়ঃ ত্রিকোনমিতিক সমীকরণ সমূহের সাধারণ সমাধান
অষ্টম অধ্যায়ঃ ত্রিকোনমিতিক সমীকরণ সমূহের সাধারণ সমাধান

সপ্তম অধ্যায়ঃ ত্রিকোণমিতিক অভেদাবলি
সপ্তম অধ্যায়ঃ ত্রিকোণমিতিক অভেদাবলি

ষষ্ট অধ্যায়ঃ অংশকোণ
ষষ্ট অধ্যায়ঃ অংশকোণ

পঞ্চম অধ্যায়ঃ গুনিতক কোণের কোণানুপাত
পঞ্চম অধ্যায়ঃ গুনিতক কোণের কোণানুপাত

চতুর্থ অধ্যায়ঃ যোগফল ও গুনফলের রূপান্তর
চতুর্থ অধ্যায়ঃ যোগফল ও গুনফলের রূপান্তর

যৌগিক কোণের কোণানুপাত ( Trigonometrical Ratios of Compound Angles )
যৌগিক কোণের কোণানুপাত ( Trigonometrical Ratios of Compound Angles )
সূচনা ( Introduction )

যে কোনো কোণ ও সংযুক্ত কোণসমূহের কোণানুপাত ( Trigonometrical Ratios of Any Angle and Associated Angles))
যে কোনো কোণ ও সংযুক্ত কোণসমূহের কোণানুপাত ( Trigonometrical Ratios of Any Angle and Associated Angles)
সূচনা (Introduction)

ধনাত্মক সূক্ষ্মকোণের ত্রিকোনমিতিক কোনানুপাত ও আদর্শ কোণসমূহ (Trigonometrical Ratios of Positive Acute Angles and Standard Angles)
ধনাত্মক সূক্ষ্মকোণের ত্রিকোনমিতিক কোনানুপাত ও আদর্শ কোণসমূহ (Trigonometrical Ratios of Positive Acute Angles and Standard Angles)<

ত্রিকোণামিতি
ত্রিকোণামিতি

লগারিদম (Logarithm)
লগারিদমের সংজ্ঞা (Definition of Logarithm), লগারিদমের সাধারণ সূত্রাবলি (General laws of logarithm), সূত্রবলিরপ্রমাণ (Proof of laws), সংক্ষিপ্তকরণ (Summarisation)

বিন্যাস ও সমবায় ( Permutation and Combination )
কতগুলি প্রদত্ত বস্তুর মধ্যে থেকে কয়েকটি বা সবগুলি একসঙ্গে নিয়ে যতভাবে সাজানো যায়, তাদের প্রত্যেকটিকে এক একটি বিন্যাস (Permutation) বলে এবং কতগুলি প্রদত্ত বস্তু থেকে কয়েকটি বা সবগুলি একসঙ্গে নিয়ে যতগুলি বিভিন্ন দল বা নির্বাচন (Group or Selection) গঠন করা হয়, তাদের প্রত্যেকটিকে এক একটি সমবায় (Combination) বলে ।

দ্বিঘাত সমীকরণের তত্ত্ব (Theory of Quadratic Equation)
যে সমীকরণে অজ্ঞাত রাশির বৃহত্তম সূচকের মান দুই হলে তাকে দুই ঘাতবিশিষ্ট বা দ্বিঘাত সমীকরণ, বীজগণিতের মৌলিক উপপাদ্য উপপাদ্য, ৩৷ কোনো দ্বিঘাত সমীকরণের দুটির বেশি বীজ থাকতে পারেনা।

সমান্তর,গুণোত্তর ও বিপরীত প্রগতি (Arithmetic, Geometric and Harmonic Progression)
এই অধ্যায়ে আমরা ধারাবাহিক সংখ্যাগুচ্ছ(sequence of numbers)বলতে কী বোঝায় তা নিয়ে আলচনা করব।একটি ধারাবাহিক সংখ্যাগুচ্ছ বলতে বোঝায় একগুচ্ছ সংখ্যা(a set of numbers)যা একটি নিয়মে ক্রমান্বয়ে সজ্জিত থাকে।
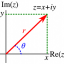
জটিল রাশি (Complex Number)
অনুবন্দী বা প্রতিযোগী জটিল রাশি (Conjugate Complex Number), জটিল রাশির মডিউলাস ও অ্যামপ্লিচিউড বা আরগুমেন্ট (Modulus and Amplitude or Argument of a Complex Number)

করণী (surds)
মূলদ সংখ্যা : যদি কোনো সংখ্যা কে p/q (p,q অখণ্ড সংখ্যা ,q≠0) আকারে প্রকাশ করা যায় তাহলে ঐ সংখ্যা কে মূলদ সংখ্যা (rational number) বা প্রমেয় রাশি (commensurable quantity) বলে।

সূচকের নিয়মাবলি (Laws of indices)
সূচকের নিয়মাবলি সূচক নিয়মাবলি (Laws of index) নিধান ও সূচক (Base and Index) যদি m একটি অখণ্ড ধনাত্মক সংখ্যা হয় তবে, এই সবক্ষেত্রে 3, x, -2 কে নিধান এবং 4, 5, 3 কে যথাক্রমে এর শক্তির সূচক বলা হয় ।

Mathematics Syllabus for Class XI
একাদশ শ্রেণীর গণিত (Mathematics) সিলেবাস, WBCHSE বোর্ড প্রদত্ত 2013 সালের আপগ্রেড সংস্করণ, PDF ফাইল সংযুক্ত করা হোলো । ডাউনলোড করতে লিঙ্কে ক্লিক করুন । ...
