1. তিনটি ভেক্টর →A=ˆi+ˆj−2ˆk, →B=ˆi−ˆj+ˆk and →C=2ˆi−3ˆj+4ˆk দেওয়া আছে । অন্য একটি ভেক্টর →X = α→A+β→B, →C এর উপর লম্ব । α এবং β দুটি সংখ্যা হলে α এবং β -র অনুপাত হবে
(A) 1 : 1 (B) 2 : 1 (C) -1 : 1 (D) 3 : 1
2. 3 µF, 6 µF এবং 6 µF ধারকত্ব বিশিষ্ট তিনটি ধারককে শ্রেণী সমবায়ে যুক্ত করে তাদের 120 V উৎসের সঙ্গে সংযুক্ত করা হল । ভোল্ট এককে ঐ 3 µF বিশিষ্ট ধারকের দুপ্রান্তে বিভব প্রভেদ হবে
(A) 24 (B) 30 (C) 40 (D) 60
3. 10 Ω আভ্যন্তরীণ রোধ বিশিষ্ট একটি গ্যালভানোমিটারে 0.01 A তড়িৎ প্রবাহ হলে পূর্ণ স্কেল বিক্ষেপণ পাওয়া যায় । এই গ্যালভানোমিটারকে একটি ভোল্টমিটারে এমন ভাবে পরিবর্তিত করা হল যে সেটি 120 V -এ পূর্ণ স্কেল বিক্ষেপণ দেয় । এর জন্য গ্যালভানোমিটারের সঙ্গে যে রোধ যুক্ত করা হল তা হচ্ছে
(A) শ্রেণী সমবায়ে 11990 Ω (B) সমান্তরাল সমবায়ে 11990 Ω
(C) শ্রেণী সমবায়ে 12010 Ω (D) সমান্তরাল সমবায়ে 12010 Ω
4. দুমুখ খোলা একটি বাঁশীতে বায়ুস্থরের মূলসুরের কম্পাঙ্ক 5100 Hz । যদি বায়ুতে শব্দের গতিবেগ 340 ms-1 হয়, তবে বাঁশীর দৈর্ঘ্য সেন্টিমিটার এককে হবে
(A) 5/3 (B) 10/3 (C) 5 (D) 20/3
5. নীচের চিত্রতে যে লজিক বর্তনী (logic circuit) দেখানো হয়েছে তার আউটপুট (output) y হবে
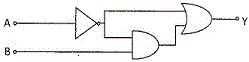
(A) ˉA+B (B) ˉA (C) ¯(ˉA+B).ˉA (D) ¯(ˉA+B).A
6. একটি এক মোল আদর্শ একপরমাণুক গ্যাসকে স্থির চাপে তাপ প্রয়োগ করে তার তাপমাত্রা 0°C থেকে 100°C করা হল । এক্ষেত্রে গ্যাসটির আভ্যন্তরীণ শক্তির পরিবর্তন হল (দেওয়া আছে R = 8.32 Jmol-1K-1)
(A) 0.83 x 10³ J (B) 4.6 x 10³ J (C) 2.08 x 10³ J (D) 1.25 x 10³ J
7. হাইড্রোজেন পরমাণুর আয়নায়ন শক্তির (ionization energy) মান 13.6 eV । এই পরমাণুর প্রথম (n = 2) উত্তেজিত স্তর থেকে ভূমি স্তরে কোনো ইলেক্ট্রনের গমনের ফলে যে ফোটন নির্গত হয় তার শক্তি হল
(A) 3.4 eV (B) 4.53 eV (C) 10.2 eV (D) 13.6 eV
8. একটি সমান্তরাল পাত ধারককে আহিত করে সরবরাহকারী ব্যাটারি থেকে বিচ্ছিন্ন করা হল । এখন অন্তরিত হাতলের সাহায্যে টান দিয়ে পাত দুটিকে যদি পরস্পরের থেকে আরও দূরে সরানো হয়, তা হলে
(A) ধারকের সঞ্চিত শক্তি হ্রাস পাবে
(B) ধারকটির ধারকত্ব বৃদ্ধি পাবে
(C) ধারকের আধান হ্রাস পাবে
(D) ধারকের দু প্রান্তের বিভব প্রভেদ বৃদ্ধি পাবে
9. যদি সরল দোলগতিতে চলমান একটি কণা ν কম্পাঙ্কে আন্দোলিত হয়, তবে কণাটির গতিশক্তি
(A) ν কম্পাঙ্কে পর্যাবৃত্তভাবে পরিবর্তিত হয়
(B) 2ν কম্পাঙ্কে পর্যাবৃত্তভাবে পরিবর্তিত হয়
(C) ν/2 কম্পাঙ্কে পর্যাবৃত্তভাবে পরিবর্তিত হয়
(D) অপরিবর্তিত থাকে
10. নীচে দেওয়া ভৌত রাশির জোড়াগুলির মধ্যে কোন জোড়াটির ভৌত রাশিদ্বয়ের মাত্রা পৃথক ?
(A) প্ল্যাঙ্কের ধ্রুবক এবং কৌণিক ভরবেগ
(B) বলের ঘাত (Impulse) এবং রৈখিক ভরবেগ
(C) জড়তা ভ্রামক এবং বলের ভ্রামক
(D) শক্তি এবং টর্ক (torque)
11. একটি ক্রিকেট বলকে মাঠের উপর ছোঁড়া হল । বলটি নিক্ষেপের t1 এবং t2 সময় পরে নিক্ষেপ বিন্দু থেকে যথাক্রমে h1 এবং h2 উচ্চতায় ছিল । একজন ফিল্ডার বলটিকে যে উচ্চতা থেকে ছোঁড়া হয়েছিল ঠিক সেই উচ্চতাতেই ধরে ফেললেন । এই যাত্রা পথে বলটির মোট যে সময় লেগেছে তা হল
(A) h1t22−h2t21h1t2−h2t1 (B) h1t21+h2t22h2t1+h1t2 (C) h1t22+h2t21h1t2+h2t1 (D) h1t21−h2t22h1t1−h2t2
12. 'a' ব্যাসার্ধের একটি ছোট ধাতব গোলক একটি উলম্ব সান্দ্র তরল স্তম্ভের মধ্য দিয়ে v গতিতে নীচে পড়ছে । এই তরল সান্দ্রতাঙ্ক η হলে ধাতব গোলকটি গতির বিপরীতে যে বল অনুভব করবে, তা হল
(A) 6πηa2v (B) 6ηvπa (C) 6πηav (D) πηv6a3
13. একজন বিজ্ঞানী একটি নতুন তাপ মাত্রার স্কেল উপস্থাপনা করে তার বরফ বিন্দু 25 X এবং বাষ্প বিন্দু 305 X হিসাবে চিহ্নিত করলেন । এখানে X হচ্ছে নতুন তাপমাত্রার একক । এই নতুন স্কেল অনুযায়ী জলের আপেক্ষিক তাপ Jkg-1X-1 এককে হবে
(A) 4.2 x 10³ (B) 3.0 x 10³ (C) 1.2 x 10³ (D) 1.5 x 10³
14. এক মোল গ্যাস নীচে দেওয়া ভ্যানডার ওয়ালসের সমীকরণ মেনে চলে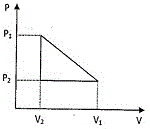
(P+aV2)(V−b)=RT
এই গ্যাসটিকে একটি প্রায় স্থির (quasi-static) আবর্ত (cyclic) প্রক্রিয়ার মধ্য দিয়ে নিয়ে যাওয়া হল যা সঙ্গের P-V লেখ চিত্রে দেখানো হয়েছে । এই প্রক্রিয়ায় গ্যাস কর্তৃক শোষিত মোট তাপের পরিমাণ হল
(A) 12(P1−P2)(V1−V2) (B) 12(P1+P2)(V1−V2)
(C) 12(P1+aV21−P2−aV22)(V1−V2) (D) 12(P1+aV21+P2+aV22)(V1−V2)
15. একটি কাঠের ব্লক বীকারে রাখা জলে ভাসছে । ব্লকটির 40% জল তলের উপরে রয়েছে । এখন বীকারটিকে একটি লিফটের মধ্যে রাখা হল এবং লিফটি g/2 ত্বরণসহ উপরের দিকে যাত্রা শুরু করল । এখন ব্লকটি
(A) ডুবে যাবে (B) 10% জলতলের উপরে রেখে ভাসবে
(C) 40% জলতলের উপরে রেখে ভাসবে (D) 70% জলতলের উপরে রেখে ভাসবে
16. একটি মসৃণ, স্থির কপিকলের (pulley) উপর দিয়ে পাঠিয়ে একটি ভরহীন মসৃণ সুতোর দুপ্রান্তে দুটি ভর m1 এবং m2 (m1 > m2) যুক্ত করা হল । এবার ভর দুটি স্থিরাবস্থা থেকে অভিকর্ষের প্রভাবে চলতে শুরু করল । এই দুটি ভরের উপর যে মোট বহিঃস্থ বল ক্রিয়া করছে তা হল
(A) (m1+m2)g (B) (m1−m2)2m1+m2g (C) (m1−m2)g (D) (m1+m2)2m1−m2g
17. একটি অমসৃণ এবং একটি ব্লকের মধ্যে স্থিত ঘর্ষণ গুণাঙ্ক পরিমাপের জন্য তলটিকে 45° নতিকোণে রাখা হল এবং ব্লকটিকে স্থিতাবস্থা থেকে ছাড়া হল । ব্লকটি d দূরত্ব অতিক্রম করতে t সময় নেয় । অমসৃণ তলটির পরিবর্তে মসৃণ তল নিয়ে একই পরীক্ষা আবার করা হল । ব্লকটি এখন t/2 সময়ে সমদূরত্ব d অতিক্রম করে । এই পরিমাপে প্রাপ্ত ঘর্ষণ গুণাঙ্ক হবে
(A) 3/4 (B) 5/4 (C) 1/2 (D) 1/√2
18. তাপীয় দৈর্ঘ্য প্রসারণ রোধ করার উদ্দেশ্যে একটি ধাতব দন্ডের দুপ্রান্ত দৃঢ়ভাবে আটকানো আছে । যদি L, α এবং γ যথাক্রমে দন্ডটির দৈর্ঘ্য, তার উপাদানের তাপীয় দৈর্ঘ্য প্রসারণ গুণাঙ্ক এবং ইয়ং গুণাঙ্ক সূচিত করে তাহলে ΔT তাপমাত্রা বৃদ্ধি ঐ দন্ডে যে অনুদৈর্ঘ্য পীড়ন সৃষ্টি করে, তা হবে
(A) α -এর ব্যস্তানুপাতিক (B) γ -এর ব্যস্তানুপাতিক (C) △Tγ -এর সমানুপাতিক (D) L নিরপেক্ষ
19. একটি কণা r ব্যাসার্ধ বিশিষ্ট বৃত্তাকার পথে সমবেগে গতিশীল । যখন কণাটি θ কৌণিক দূরত্ব গমন করে তখন সংশ্লিষ্ট রৈখিক সরণের মান হবে
(A) 2rcos(θ2) (B) 2rcot(θ2) (C) 2rtan(θ2) (D) 2rsin(θ2)
20. একটি সুষম দন্ডকে তার মধ্যবিন্দু থেকে অনুভূমিক ভাবে ঝোলানো হল । মধ্যবিন্দু থেকে l দূরত্বে W ভরের একটি ধাতুখন্ড ঝোলানো হল । বিপরীত দিকে W1 ভরকে মধ্যবিন্দু থেকে l1 দূরত্বে ঝোলানো হলে দন্ডটি অনুভূমিক অবস্থায় চলে এলো । এখন W কে জলে সম্পূর্ণ নিমজ্জিত করলে এবং W1 কে মধ্যবিন্দু থেকে l2 দূরত্বে রাখলে আবার দন্ডটি অনুভূমিক অবস্থায় আসে । ধাতুখন্ডটির আপেক্ষিক গুরুত্ব হবে
(A) WW1 (B) Wl1Wl−W1l2 (C) l1l1−l2 (D) l1l2
21. কোনো একটি তরলের 0.04 cm³ আয়তন বিশিষ্ট একটি ফোঁটা একটি কাঁচের স্লাইডের তলের উপর রাখা হল । এর পর আরেকটি কাঁচের স্লাইড প্রথমটির উপর এমনভাবে বসানো হল যে তরলটি দুটি স্লাইডের তলের মাঝখানে 20 cm² ক্ষেত্রবিশিষ্ট একটি পাতলা স্তর তৈরী করল । স্লাইড দুটিকে আলাদা করতে 16 x 105 dyne বল তলের উপর লম্বভাবে প্রয়োগ করতে হয় । তা হলে তরলটির পৃষ্ঠটান হবে ( dyne-cm-1 -এ )
(A) 60 (B) 70 (C) 80 (D) 90
22. একটি ইলেকট্রন .05 nm ব্যাসার্ধ বিশিষ্ট একটি বৃত্তাকার পথে সেকেন্ডে 1016 বার আবর্তন করছে । ইলেক্ট্রনের এই ঘুর্ণনের জন্য Am² এককে যে চৌম্বক ভ্রামক তৈরী হবে তা হল
(A) 2.16 x 10-23 (B) 3.21 x 10-22 (C) 3.21 x 10-24 (D) 1.26 x 10-23
23. একটি খুব ছোট a ব্যাসার্ধ বিশিষ্ট বৃত্তাকার লুপ (loop) বা কুন্ডলী তুলনায় অনেক বড় b ব্যাসার্ধ বিশিষ্ট একটি বৃত্তাকার কুন্ডলীর সাথে প্রারম্ভিক ভাবে ( t = 0 ) একই তলে সমকেন্দ্রিক ভাবে রাখা আছে । স্থির মানের তড়িৎ প্রবাহ I বড় কুণ্ডলীটির মধ্য দিয়ে পাঠানো হচ্ছে এবং কুন্ডলীটির একটি তলের উপর আটকানো আছে । কুন্ডলীটির সাধারণ ব্যাসকে অক্ষ ধরে ছোট কুন্ডলীটিকে সুষম কৌণিক গতিবেগে ω -তে ঘোরানো হচ্ছে । ছোট কুন্ডলীতে সময় t -এর সাপেক্ষে তড়িচ্চালক বল হচ্ছে
(A) πa2μ0I2bωcos(ωt) (B) πa2μ0I2bωsin(ω2t2)
(C) πa2μ0I2bωsin(ωt) (D) πa2μ0I2bωsin2(ωt)
24. একটি উজ্জ্বল বস্তু একটি পর্দা থেকে d দূরত্বে রাখা আছে । একটি উত্তল লেন্স এই বস্তু এবং পর্দার মধ্যবর্তী অঞ্চলে রাখার ফলে পর্দার উপর বস্তুটির একটি স্পষ্ট প্রতিবিম্ব গঠিত হল । এই উত্তল লেন্সের ফোকাস দূরত্বের সর্বোচ্চ সম্ভাব্য মান
(A) 4d (B) 2d (C) d/2 (D) d/4
25. অসীমবিস্তৃত একটি তলের উপর আধানের তলমাত্রিক সুষম ঘনত্ব σ এবং তা xy -তলে অবস্থিত । একটি বিন্দু →A=a(ˆi+2ˆj+3ˆk) থেকে অপর একটি বিন্দু →B=a(ˆi−2ˆj+6ˆk) -তে (যেখানে a দৈর্ঘ্যের মাত্রা সম্বলিত একটি ধ্রুবক এবং ε0 শূন্য মাধ্যমের তড়িৎভেদ্যতা ) q পরিমাণ আধানকে নিয়ে যেতে যে কাজ করতে হবে তা হল
(A) 3σaq2ϵ0 (B) 2σaqϵ0 (C) 5σaq2ϵ0 (D) 3σaqϵ0
26. একটি দন্ড চুম্বকের মাত্রা 5.0 x 104 Am-1. চুম্বকটির চৌম্বকীয় দৈঘ্য এবং প্রস্থচ্ছেদের ক্ষেত্রফল যথাক্রমে 12 cm and 1 cm² । এই দন্ড চুম্বকটির চৌম্বক ভ্রামকের মান SI এককে হবে
(A) 0.6 (B) 1.3 (C) 1.24 (D) 2.4
27. একটি বস্তুকণা স্থিরাবস্থা থেকে যাত্রা শুরু করে সরলরেখা বরাবর সমত্বরণে চলেছে । বস্তুকণা কর্তৃক চতুর্থ সেকেন্ডে অতিক্রান্ত দূরত্ব তৃতীয় সেকেন্ডে অতিক্রান্ত দূরত্বের তুলনায় শতকরা যতটা বেশী হবে তা হল
(A) 33% (B) 40% (C) 66% (D) 77%
28. m ভর এবং q আধান সম্পন্ন একটি প্রোটন E গতিশক্তি নিয়ে একটি তলের উপর চলেছে । যদি এই তলটির লম্বাভিমুখে B মানের একটি সুষম চৌম্বক ক্ষেত্র থাকে তাহলে প্রোটনটি একটি বৃত্তাকার পথে চলবে এবং ঐ বৃত্তের ব্যাসার্ধ হবে
(A) 2EmqB (B) √2EmqB (C) √Em2qB (D) √2EqmB
29. একটি কৃত্রিম উপগ্রহ পৃথিবীর চারিদিকে বৃত্তাকার কক্ষপথে আবর্তিত হচ্ছে । উপগ্রহটির মোট শক্তির মান E দিয়ে সূচিত হলে উপগ্রহটির স্থিতিশক্তি হবে
(A) -2E (B) 2E (C) 2E/3 (D) -2E/3
30. নীচের কোন পরিঘটনার ক্ষেত্রে তাপ তরঙ্গ আলোর গতিতে সরলরেখায় গমন করে ?
(A) তাপের পরিবহন (B) তাপের পরবশ (forced) পরিচলন (C) তাপের স্বাভাবিক পরিচলন (D) তাপের বিকিরণ
31. কোনো একটি উপাদানের যোজ্যতা পটি (valence band) এবং পরিবাহী পটির (conduction band) মধ্যবর্তী শক্তি ব্যবধান (band gap) 5.0 eV । এই উপাদানটি একটি
(A) অর্ধপরিবাহী (B) সুপরিবাহী (C) অতিপরিবাহী (D) অন্তরক
32. একটি নিরেট সুষম গোলাকৃতি বল একটি মসৃণ নততল বরাবর h উচ্চতা থেকে গড়িয়ে নামছে । নততলের নীচপ্রান্তে পৌঁছে এই বলটি v গতিবেগ লাভ করে । এবার এই বলটিকে যদি v গতিবেগ দিয়ে উলম্বভাবে ওপরদিকে ছোঁড়া যায়, তা হলে বলটি সর্বোচ্চ যে উচ্চতায় উঠবে তা হল
(A) 5h/8 (B) 3h/5 (C) 5h/7 (D) 7h/9
33. যথাক্রমে I এবং 4I প্রাবল্য বিশিষ্ট একবর্ণী আলোর দুটি সুসংগত ( coherent ) তরঙ্গের উপরিপাত ঘটল । এর ফলে যে লব্ধি প্যাটার্ন (pattern) সৃষ্টি হল সেখানে সর্বোচ্চ ও সর্বনিম্ন প্রাবল্য যথাক্রমে হবে
(A) 5 I and 3 I (B) 9 I and 3 I (C) 4 I and I (D) 9 I and I
34. এখানে দেওয়া বর্তনীটিতে যখন Vi -কে 2V থেকে 6V -এ বৃদ্ধি করা হল তখন যে প্রবাহমাত্রার পরিবর্তন ঘটবে mA এককে তার মান হবে (ডায়োডটিকে আদর্শ ডায়োড হিসাবে ধরে নাও )
![]()
(A) শূন্য (B) 20 (C) 80/3 (D) 40
35. (nh2πqB) রাশিটিতে n একটি অখন্ড ধনাত্মক সংখ্যা, h প্ল্যাঙ্কের ধ্রুবক, q আধান এবং B চৌম্বক ক্ষেত্র সূচিত করে । রাশিটির মাত্রা হয়
(A) ক্ষেত্রফলের (B) দৈর্ঘ্যের (C) দ্রুতির (D) ত্বরণের
36. সচরাচর ব্যবহৃত কোন ট্রানজিস্টারের সাধারণ নিঃসারক ( common emitter ) সংযোগে আউটপুট বৈশিষ্ট্যের সক্রিয় অঞ্চলে ( active region ) ভূমি প্রবাহ IB, সংগ্রাহক Ic এবং সংগ্রাহক-নিঃসারক ভোল্টেজ Vce -এর মানগুলি হয়
(A) IB এবং Ic উভয়েই µA -এ এবং Vce ভোল্ট -এ
(B) IB µA -এ Ic mA -এ এবং Vce ভোল্ট -এ
(C) IB mA -এ Ic µA -এ এবং Vce mV -এ
(D) IB mA -এ Ic mA -এ এবং Vce mV -এ
37. পর্যাবৃত্ত গতিতে চলমান একটি বস্তুকণার সরণ y=4cos2(t2)sin(1000t) সমীকরণ দ্বারা প্রকাশ করা যায় । এই সরণটিকে n সংখ্যক স্বাধীন দোলগতির উপরিপাত হিসাবে দেখা সম্ভব । সে ক্ষেত্রে n হবে
(A) 1 (B) 2 (C) 3 (D) 4
38. একটি ঘনকাকৃতি বাক্সে পরম তাপমাত্রা T তে কৃষ্ণ বিকিরণ রয়েছে । যদি বাক্সটির প্রতিটি বাহুর দৈর্ঘ্য দ্বিগুণ করা হয় এবং বাক্সটির দেওয়াল এবং বিকিরণের তাপমাত্রা অর্ধেক করা হয় তা হলে প্রারম্ভিকের তুলনায় অন্তিম বিকিরণ শক্তি
(A) অর্ধেক হবে (B) দ্বিগুণ হবে (C) চতুর্গুণ হবে (D) অপরিবর্তিত থাকবে
39. দুটি গোলকাকৃতি সমকেন্দ্রিক ধাতব গোলকের ব্যাসার্ধ যথাক্রমে r1 এবং r2 (r2 > r1) । ভেতরের গোলকটিকে ভূমির সঙ্গে যুক্ত করে বহিঃস্থ গোলকটিকে q পরিমাণ আধান দেওয়া হল । আভ্যন্তরীণ গোলকের ওপর আধানের পরিমাণ হবে
(A) −r2r1q (B) শূন্য (C) −r1r2q (D) - q
40. তড়িচ্চালক বল E এবং আভ্যন্তরীণ রোধ r বিশিষ্ট চারটি তড়িৎ কোষকে শ্রেণী সমবায়ে একটি বহিঃস্থ রোধ R -এর সঙ্গে যুক্ত করা হল । এগুলির মধ্যে একটি কোষকে ভুল করে বিপরীত ভাবে যুক্ত করা হয়েছে । সেক্ষেত্রে বহিঃস্থ বর্তনীতে প্রবাহমাত্রা হবে
(A) 2E4r+R (B) 3E4r+R (C) 3E3r+R (D) 2E3r+R
41. একই আকার ও আকৃতি এবং সমান পুরু দেওয়াল সম্পন্ন কিন্তু ভিন্ন উপাদানে তৈরী দুটি পাত্র P এবং Q -তে সমপরিমাণ বরফ ভর্তি করা হল । দুটি পাত্রকে একই পরিমন্ডলে (surroundings) রাখা হল । যদি P পাত্রে t1 সময়ে সম্পূর্ণ বরফ গলে যায় এবং Q -তে তা ঘটতে t2 সময় লাগে তা হলে P এবং Q -এর উপাদানের তাপ পরিবাহিতাঙ্কের অনুপাত হবে
(A) t2:t1 (B) t1:t2 (C) t21:t22 (D) t22:t21
42. যে সব তেজষ্ক্রিয় কেন্দ্রক α (আলফা) অথবা ß (বিটা) বিঘটনের মধ্য দিয়ে ভেঙ্গে যায় সেগুলির ক্ষেত্রে নীচের কোনটি ঘটতে পারে না ?
(A) মূল কেন্দ্রকের আইসোবার তৈরী হয়
(B) মূল কেন্দ্রকের আইসোটোপ তৈরী হয়
(C) মূল কেন্দ্রকের তুলনায় উচ্চতর পারমাণবিক সংখ্যার কেন্দ্রক তৈরী হয়
(D) মূল কেন্দ্রকের তুলনায় নিম্নতর পারমাণবিক সংখ্যার কেন্দ্রক তৈরী হয়
43. 72 km-hour-1 দ্রুতিতে একটি গাড়ি রাস্তার পাশে রাখা একটি শব্দের উৎসের দিকে এগিয়ে চলেছে । উত্স থেকে 850 Hz কম্পাঙ্কের শব্দ নিঃসারিত হচ্ছে । গাড়ির চালক ঐ উৎসের অভিমুখে যাওয়ার সময় শব্দটি শুনতে পান এবং উৎসটি অতিক্রম করে দূরে চলে যাওয়ার সময়ও তিনি শব্দটি শোনেন । দুটি ক্ষেত্রে তিনি দুটি ভিন্ন কম্পাঙ্কের শব্দ শোনেন । যদি বায়ুতে শব্দের গতিবেগ 340 ms-1 হয় তবে ঐ কম্পাঙ্কদ্বয়ের পার্থক্য হবে
(A) 50 Hz (B) 85 Hz (C) 100 Hz (D) 150 Hz
44. একটি গামা (γ) রশ্মি ফোটনের শক্তি Eγ এবং একটি এক্স X রশ্মি ফোটনের শক্তি Ex । যদি দৃষ্টি গ্রাহ্য (visible) আলোর ফোটনের শক্তি Ev হয় তা হলে বলা যায় যে
(A) Ex > Eγ > Ev (B) Eγ > Ev > Ex (C) Eγ > Ex > Ev (D) Ex > Ev > Eγ
45. যৌগিক অণুবীক্ষণ যন্ত্রে অভিলক্ষ্য (objective) যে অন্তর্বর্তী প্রতিবিম্ব গঠন করে সেটি হল,
(A) সদ্ , অবশীর্ষ এবং বিবর্ধিত (B) সদ্ , সমশীর্ষ এবং বিবর্ধিত (C) অসদ্ , সমশীর্ষ এবং বিবর্ধিত (D) অসদ্ , অবশীর্ষ এবং বিবর্ধিত
46. একটি নিরেট সুষম গোলক একটি অমসৃণ অনুভূমিক তলের উপর স্থিরাবস্থায় রয়েছে । গোলকটিতে তার কেন্দ্রগামী রেখা বরাবর অনুভূমিক দিকে একটি ঘাত প্রয়োগ করা হল । এর ফলে একটি প্রারম্ভিক গতিবেগ vo নিয়ে তলের উপর পিছলে চলতে শুরু করল । যখন না পিছলে গড়িয়ে ঘুরতে ঘুরতে চলতে শুরু করবে তখন গোলকটির কেন্দ্রের গতি হবে
(A) 27v0 (B) 37v0 (C) 57v0 (D) 67v0
47. একটি ইলেকট্রনের ডি ব্রগলি (de Broglie) তরঙ্গদৈর্ঘ্য 50 keV -র X রশ্মি ফোটনের তরঙ্গদৈর্ঘ্যের সমান । এই ফোটনের শক্তি এবং ইলেকট্রনের গতিশক্তির অনুপাত হবে (দেওয়া আছে ইলেকট্রন ভরের সমতুল শক্তি 0.5 MeV)
(A) 1 : 50 (B) 1 : 20 (C) 20 : 1 (D) 50 : 1
48. একটি কাঁচের ফলক (slab) অনেকগুলি পাতলা স্তর দিয়ে এমন ভাবে গঠিত যে একটি স্তর অপেক্ষা তার উপরের স্তরের প্রতিসরাঙ্ক ক্রমশ কমে গেছে (চিত্রে দেখো ) । প্রতিসরাঙ্ক μ-mΔμ সূত্রানুযায়ী হ্রাস পায় । এখানে μ , Δμ যথাক্রমে শূন্যতম ( 0th ) স্তরের প্রতিসরাঙ্ক এবং দুটি সন্নিবিষ্ট স্তরের মধ্যে প্রতিসরাঙ্কের পার্থক্য । অখন্ড সংখ্যা m স্তর সংখ্যা ( m = 0,1,2,3...) সূচিত করে । শূন্যতম স্তর থেকে প্রথম স্তরে প্রবেশের সময় একটি রশ্মির আপতন কোণ 30° । যদি μ = 1.5 এবং Δμ = 0.015 হয় তবে m এর কোন মানের জন্য m -তম প্রতিসরণের পর রশ্মিটি দুটি স্তরের বিভেদ তলের সমান্তরাল ভাবে নির্গত হবে ?
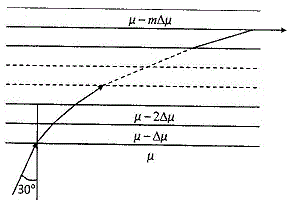
(A) 20 (B) 30 (C) 40 (D) 50
49. একটি লম্বা পরিবাহী তারের মধ্যে দিয়ে I তড়িৎ প্রবাহিত হচ্ছে । তারটি 120° কোণে বাঁকানো আছে । চিত্রে প্রদর্শিত কোণটির সমদ্বিখন্ডকের উপর ভাঁজটি (bend) থেকে d দূরত্বে অবস্থিত P বিন্দুতে চৌম্বক ক্ষেত্র B হচ্ছে (μ0 শূন্য মাধ্যমের চুম্বক ভেদ্যতা)
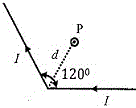
(A) 3μ0I2πd (B) μ0I2πd (C) μ0I√3πd (D) √3μ0I2πd
50. চিত্রে প্রদর্শিত তিনটি তড়িৎকোষের তড়িচ্চালক বল E1 = 1 V, E2 = 2 V ও E3 = 3 V এবং এদের আভ্যন্তরীণ রোধ যথাক্রমে 1Ω, 2Ω ও 1Ω । এগুলিকে চিত্রানুযায়ী সমান্তরাল সমবায়ে যুক্ত করা হয়েছে । এ ক্ষেত্রে P এবং Q বিন্দুর মধ্যে বিভব প্রভেদ হবে
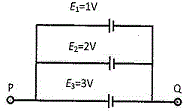
(A) 1.0 V (B) 2.0 V (C) 2.2 V (D) 3.0 V
51. চিত্রে দেখানো ব্যবস্থা অনুযায়ী শব্দ তরঙ্গ দুটি নলের পথে যাচ্ছে । একটি পথ সরল রৈখিক, অন্যটি r ব্যাসার্ধ বিশিষ্ট উপবৃত্তাকার পথ । তরঙ্গদুটি আবার মিলিত হচ্ছে ও তাদের উপরিপাত ঘটছে । নলের মধ্যে বাতাসে শব্দের গতিবেগ v । যে কম্পাঙ্কের জন্য লব্ধি তরঙ্গগুলির বিস্তার সর্বোচ্চ হবে সেটি নিম্নলিখিত কোন রাশিটির অখন্ড ধনাত্মক গুণিতক ?

(A) vr(π−2) (B) vr(π−1) (C) 2vr(π−1) (D) vr(π+1)
52. একটি দ্বিধাতব সংকর ধাতুর উপাদানগত গঠন নির্ণয়ের জন্য ধাতুটির একখন্ড নমুনা নিয়ে তাকে বায়ুতে এবং তারপর জলে ওজন করা হল । এই ওজন দুটি যথাক্রমে w1 এবং w2 । সংকর গঠনকারী ধাতু দুটির ঘনত্ব যথাক্রমে ρ1 এবং ρ2 এবং জলের ঘনত্ব ρw হলে ঐ সংকর উপাদানে উপস্থিত প্রথম ধাতুটির ওজন হবে
(A) ρ1ρw(ρ2−ρ1)[w1(ρ2−ρw)−w2ρ2]
(B) ρ1ρw(ρ2+ρ1)[w1(ρ2−ρw)+w2ρ2]
(C) ρ1ρw(ρ2−ρ1)[w1(ρ2+ρw)−w2ρ1]
(D) ρ1ρw(ρ2−ρ1)[w1(ρ1−ρw)−w2ρ1]
53. একটি পাত্রে 0.5 kg জল রেখে তাকে 10 W -এর একটি বৈদ্যুতিক হিটারের সাহায্যে গরম করা হল । দেখা গেল যে জল ও পাত্রের তাপমাত্রা 15 মিনিটে 3°K বৃদ্ধি পেয়েছে । ঐ পাত্রকে তারপর খালি ও শুষ্ক করে সেখানে 2 kg তেল নেওয়া হল । আবার ঐ একই হিটারে 20 মিনিট তেল ও পাত্রের তাপমাত্রা 2°K বৃদ্ধি করল । যদি ধরে নেওয়া হয় যে কোন তাপের অপচয় হয় নি এবং জলের আপেক্ষিক তাপ 4200 Jkg-1K-1 হয়, তা হলে একই এককে তেলের আপেক্ষিক তাপ হবে
(A) 1.50 x 10³ (B) 2.55 x 10³ (C) 3.00 x 10³ (D) 5.10 x 10³
54. 10 cm ফোকাস দূরত্ব বিশিষ্ট একটি উত্তল লেন্সের থেকে 30 cm দূরত্বে একটি বস্তুর স্পষ্ট প্রতিবিম্ব একটি পর্দায় গঠিত হল । এখন একটি অবতল লেন্সকে ঐ উত্তল লেন্সকে স্পর্শ করে রাখা হল এবং এ ক্ষেত্রে পর্দাটিকে 45 cm সরিয়ে ঐ একই বস্তুর স্পষ্ট প্রতিবিম্ব ধরা গেল । ঐ অবতল লেন্সের ফোকাস দূরত্বের মান cm এককে হবে
(A) 72 (B) 60 (C) 36 (D) 20
55. তিনটি অবিকল একরকম বর্গাকৃতি পাত চিত্রে দেখানো অক্ষ বরাবর এমন ভাবে ঘুরছে যে তাদের প্রত্যেকের গতিশক্তি সমান । প্রতি ক্ষেত্রেই ঘূর্ণন অক্ষ পাতের কেন্দ্র দিয়ে যাচ্ছে । সেক্ষেত্রে তিনটির ঘূর্ণন গতিবেগের অনুপাত ω1 : ω2 : ω3 হবে
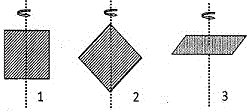
(A) 1 : 1 : 1 (B) √2 : √2 : 1 (C) 1 : √2 : 1 (D) 1 : 2 : √2
56. তাপরুদ্ধ একটি চোঙের সঙ্গে A প্রস্থচ্ছেদ ও m ভর বিশিষ্ট একটি ঘর্ষণহীন পিস্টন যুক্ত করা রয়েছে । চোঙের মধ্যে চিত্রানুযায়ী r রোধবিশিষ্ট একটি রোধক তাপ সরবরাহের জন্য রাখা আছে । এই চোঙটির মধ্যে এক মোল আদর্শ দ্বিপরমাণুক গ্যাস রয়েছে । রোধকটির মধ্য দিয়ে বিদ্যুৎ প্রবাহ পাঠালে সময়ের (t) সঙ্গে তাপমাত্রার পরিবর্তন ΔT=αt+12βt2 সম্পর্কানুযায়ী ঘটে এবং চাপ অপরিবর্তিত থাকে (α এবং ß দুটি ধ্রুবক সংখ্যা ) । যদি পিস্টনের উপর বায়ুমন্ডলের চাপ P0 হয় তবে
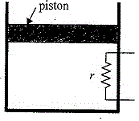
(A) গ্যাসের আভ্যন্তরীণ শক্তির বৃদ্ধির হার 52R(α+βt)
(B) রোধকটির মধ্য দিয়ে যে প্রবাহমাত্রা যাচ্ছে তার মান √52rR(α+βt)
(C) পিস্টনটি উপরের দিকে সমত্বরণে উঠতে থাকে
(D) পিস্টনটি উপরের দিকে সমদ্রুতিতে উঠতে থাকে
57. একটি সরু দন্ড AB -কে অনুভূমিক অবস্থায় এমন ভাবে রাখা আছে যে দন্ডটি চিত্রানুযায়ী A প্রান্তের সাপেক্ষে বিনা বাধায় উলম্ব তলে ঘুরতে পারে । এই দন্ডটি যখন উলম্বভাবে ঝোলে তখন তার স্থিতিশক্তি শূন্য ধরা হল । দন্ডটির B প্রান্তকে স্থিতাবস্থায় অনুভূমিক অবস্থান থেকে ছেড়ে দেওয়া হল । যে মুহুর্তে দন্ডটি অনুভূমিক দিকের সঙ্গে দিকের θ কোণ করছে (চিত্রে দেখ) তখন
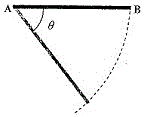
(A) B প্রান্তের দ্রুতি √sinθ -র সমানুপাতিক
(B) দন্ডটির স্থিতিশক্তি (1 - cos θ) -র সমানুপাতিক
(C) দন্ডটির কৌণিক ত্বরণ cos θ -র সমানুপাতিক
(D) A বিন্দুর সাপেক্ষে টর্ক (torque) তার প্রারম্ভিক মানের সঙ্গে সমান থাকে
58. আলোক তড়িৎ ক্রিয়া বিষয়ক নিম্নলিখিত বিবৃতিগুলির মধ্যে সঠিকটি /সঠিকগুলি চিহ্নিত কর
(A) উপযুক্ত বিকিরণের শোচন এবং ইলেক্ট্রনের নিঃসরণের মধ্যে কোনো উল্লেখযোগ্য সময়ের ব্যবধান থাকে না
(B) আইনস্টাইন বিশ্লেষণ যে প্রারম্ভ কম্পাঙ্ক চিহ্নিত করে তার থেকে বেশী কম্পাঙ্কের বিকিরণে কোনো ইলেকট্রন নিঃসরণ ঘটে না
(C) নিঃসারিত আলোক-ইলেক্ট্রনের সর্বোচ্চ গতিশক্তি আপতিত বিকিরণের কম্পাঙ্কের সমানুপাতিক
(D) ইলেক্ট্রনের সর্বোচ্চ গতিশক্তি বিকিরণের প্রাবল্যের ওপর নির্ভর করে না
59. একটি সমান্তরাল পাত ধারকের পাতদুটির মধ্যবর্তী অংশের অর্ধেক K পরাবৈদ্যুতিক ধ্রুবক বিশিষ্ট উপাদান দিয়ে ভর্তি করা হয়েছে এবং বাকি অংশে রয়েছে বায়ু (চিত্রে দেখ) । ধারকে এখন Q আধান সরবরাহ করা হল । এ ক্ষেত্রে
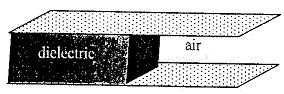
(A) পরাবৈদ্যুতিক উপাদানপূর্ণ অংশে বিদ্যুৎক্ষেত্র বায়ুপূর্ণ অংশের তুলনায় বেশী
(B) নীচের পাতের দুটি অর্ধাংশের আধান-ঘনত্ব অসমান
(C) উপরের পাতের যে অর্ধাংশ বায়ুপূর্ণ অংশের উপরে রয়েছে সেখানে আধান হবে QK+1
(D) চিত্রে প্রদর্শিত ধারকটির ধারকত্ব হবে (1+K)C02 যেখানে C0 হচ্ছে পরাবৈদ্যুতিক মাধ্যম সরিয়ে নেওয়ার পরে ঐ একই ধারকের ধারকত্ব
60. একটি পর্দার উপর রাখা একটি সরু রেখাছিদ্রের (slit) দিকে ইলেকট্রন ও প্রোটনের ধারা পাঠানো হচ্ছে (চিত্রে দেখ) মধ্যবর্তী অঞ্চলে একটি সুষম বৈদ্যুতিক ক্ষেত্র →E (উলম্বভাবে নীচের দিকে ) এবং একটি সুষম চুম্বক ক্ষেত্র →B (চিত্রের তলের সাপেক্ষে বাইরের দিকের অভিমুখে ) কাজ করছে । সে ক্ষেত্রে

(A) যে সমস্ত ইলেকট্রন ও প্রোটনের দ্রুতি |→E||→B|, তারা রেখাছিদ্রের মধ্যে দিয়ে যাবে
(B) |→E||→B| দ্রুতিসম্পন্ন প্রোটন রেখাছিদ্রের মধ্যে দিয়ে যাবে কিন্তু একই দ্রুতির ইলেকট্রন যাবে না
(C) ইলেকট্রন বা প্রোটন কেউই ঐ রেখাছিদ্র দিয়ে যেতে পারবে না, তাদের দ্রুতি যাই হোক না কেন
(D) ইলেকট্রনের দ্রুতি যাই হোক না কেন তারা সর্বদাই উপরের দিকে বিচ্যুত হয়ে যাবে
***






